
- •2 . Основы теории четырёхполюсников
- •2.1. Основные определения и классификация четырехполюсников
- •2.2. Вывод уравнений пассивного четырехполюсника
- •2.3. Эквивалентные схемы замещения активного четырехполюсника
- •2.8. Характеристические параметры пассивных четырехполюсников. Уравнение четырехполюсника в гиперболических функциях.
- •3.1. Частотные элетрические цепи. Электрические фильтры и их классификация. Полоса пропускания и непропускания.
- •4.1.Общая характеристика нелинейных электрических цепей.
- •4 .2. Статические и дифференциальные параметры нелинейных элементов
- •4.3. Графические методы расчета
- •4.3.1. Последовательное соеденинене
- •4.3.2. Параллельное соединение
- •4.3.3. Последовательное – параллельное соединение линейных и нелинейных эл. Цепей
- •4.4.1. Графоаналитические методы расчеты. Метод линеаризации.
- •4.4.2. Графоаналитические методы расчеты. Метод эквивалентного генератора.
- •4.4.3. Графоаналитические методы расчеты. Метод двух узлов
- •4.5.4.1. Расчет нелинейных электрических цепей при синусоидальных воздействиях. Метод кусочно – линейной аппроксимации.
- •4.5.4.4. Расчет нелинейных электрических цепей при синусоидальных воздействиях. Метод эквивалентных синусоид. Линеаризация задачи в методе эквивалентных синусоид.
- •4.5.4.5. Расчет нелинейных электрических цепей при синусоидальных воздействиях. Расчет электрической цепи, содержащей катушку с ферромагнитным сердечником методом эквивалентных синусоид.
- •4.5.5.1. Резонанс в нелинейных цепях : Феррорезонанс напряжений.
- •5.1. Магнитные цепи: Основные величины, характеризующие магнитное поле.
- •5.2. Магнитные цепи: Основные законы магнитной цепи.
- •6.1. Расчет переходных процессов в нелинейных электрических цепях: Общая характеристика переходных процессов в нелинейных электрических цепях.
- •6.2. Расчет переходных процессов в нелинейных электрических цепях: Графоаналитически метод расчета.
- •6.3. Расчет переходных процессов в нелинейных электрических цепях: Метод кусочно – линейной аппроксимации.
- •6.4. Расчет переходных процессов в нелинейных электрических цепях: Метод графического интегрирования
- •6.5. Расчет переходных процессов в нелинейных электрических цепях: Метод траекторий в пространстве состояний.
- •9. Электрические машины постоянного тока: устройство и принцип действия машин постоянного тока; механические характеристики кпд машин постоянного тока.
- •Устройство машин постоянного тока
- •Принцип действия машин постоянного тока
- •10. Электрические машины переменного тока: устройство и принцип действия машин переменного тока; механические характеристики и кпд машин переменного тока.
- •11. Информационные электрические машины: поворотные трансформаторы, сельсины, тахогенераторы, шаговые двигатели – назначение и основные параметры
2.3. Эквивалентные схемы замещения активного четырехполюсника
Как было отмечено ранее, пассивный четырехполюсник характеризуется тремя независимыми постоянными коэффициентами. Следовательно, пассивный четырехполюсник можно представить в виде трехэлементной эквивалентной Т- (рис. 3,а) или П-образной (рис. 3,б) схемы замещения.
Для определения коэффициентов четырехполюсника для схемы на рис. 3,а с использованием первого и второго законов Кирхгофа выразим и через и :

|
(9) |
|
(10) |
Сопоставление полученных выражений (9) и (10) с соотношениями (3) и (4) дает:
![]()
Данная
задача может быть решена и другим путем.
При
![]() (холостой
ход со стороны вторичных зажимов) в
соответствии с (3) и (4)
(холостой
ход со стороны вторичных зажимов) в
соответствии с (3) и (4)
![]() и
и ![]() ;
;
но из схемы на рис. 3,а
![]() , а
, а ![]() ;
;
откуда
вытекает:
![]() и
и
![]() .
.
При
![]() (короткое
замыкание на вторичных зажимах)
(короткое
замыкание на вторичных зажимах)
![]() и
и ![]() .
.
Из схемы на рис. 3,а
![]() ;
;
![]() .
.
Следовательно,
![]()
![]() .
.
2.8. Характеристические параметры пассивных четырехполюсников. Уравнение четырехполюсника в гиперболических функциях.
В электросвязи широко используется режим работы симметричного четырехполюсника, при котором его входное сопротивление равно нагрузочному, т.е.
![]() .
.
Это
сопротивление обозначают как
![]() и
называют характеристическим
сопротивлением симметричного
четырехполюсника, а режим работы
четырехполюсника, для которого
справедливо
и
называют характеристическим
сопротивлением симметричного
четырехполюсника, а режим работы
четырехполюсника, для которого
справедливо
![]() ,
,
называется режимом согласованной нагрузки.
В
указанном режиме для симметричного
четырехполюсника
![]() на
основании (3) и (4) можно записать
на
основании (3) и (4) можно записать
|
(13) |
|
(14) |
Разделив соотношение (13) на (14), получаем уравнение
![]() ,
,
решением которого является
|
(15) |
С учетом (15) уравнения (13) и (14) приобретают вид
![]() ;
;
![]() .
.
Таким образом,
![]() ,
,
где
![]() -
коэффициент
распространения(передачи);
-
коэффициент
распространения(передачи);
![]() -
коэффициент
затухания (измеряется
в неперах);
-
коэффициент
затухания (измеряется
в неперах);
![]() -
коэффициент
фазы (измеряется
в радианах).
-
коэффициент
фазы (измеряется
в радианах).
Запишем уравнение симметричного четырехполюсника с использованием коэффициента распространения.
По определению
|
(16) |
Тогда
|
(17) |
Решая
(17) и (18) относительно
![]() и
и
![]() ,
получим
,
получим
![]() и
и ![]() .
.
Учитывая, что
![]()
и
![]() ,
,
получаем уравнения четырехполюсника, записанные через гиперболические функции:
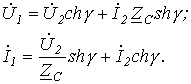
3.1. Частотные элетрические цепи. Электрические фильтры и их классификация. Полоса пропускания и непропускания.
Электрическим фильтром частотно-изберательная цепь, которая служит для выделения полезных сигналов на фоне различных помех и используется при обработке сигнала. В основу работы ЭФ положены следующие условия:
1.Сопротивление катушки индуктивности пропорционально частоте, а напряжение на выходах опережает ток на 90 градусов. ХL=wL, φ=90
2. ХC=1/wC, φ= -90
Диапазон частот, пропускаемых фильтром без затухания (с малым затуханием), называется полосой пропускания или полосой прозрачности; диапазон частот, пропускаемых с большим затуханием, называется полосой затухания или полосой задерживания. Качество фильтра считается тем выше, чем ярче выражены его фильтрующие свойства, т.е. чем сильнее возрастает затухание в полосе задерживания.
В качестве пассивных фильтров обычно применяются четырехполюсники на основе катушек индуктивности и конденсаторов. Возможно также применение пассивных RC-фильтров, используемых при больших сопротивлениях нагрузки.
Фильтры применяются как в радиотехнике и технике связи, где имеют место токи достаточно высоких частот, так и в силовой электронике и электротехнике.
Для
упрощения анализа будем считать, что
фильтры составлены из идеальных катушек
индуктивности и конденсаторов, т.е.
элементов соответственно с нулевыми
активными сопротивлением и проводимостью.
Это допущение достаточно корректно
при высоких частотах, когда индуктивные
сопротивления катушек много больше их
активных сопротивлений (
![]() ),
а емкостные проводимости конденсаторов
много больше их активных проводимостей
(
),
а емкостные проводимости конденсаторов
много больше их активных проводимостей
(
![]() ).
).
Фильтрующие
свойства четырехполюсников обусловлены
возникающими в них резонансными режимами
– резонансами токов и напряжений.
Фильтры обычно собираются по симметричной
Т- или П-образной схеме, т.е. при
![]() или
или
![]() (см.
лекцию №14). В этой связи при изучении
фильтров будем использовать понятия
коэффициентов затухания и фазы g=a+jb
– коэффициент передачи, а – к-т затухания,
b – к-т фазы.
(см.
лекцию №14). В этой связи при изучении
фильтров будем использовать понятия
коэффициентов затухания и фазы g=a+jb
– коэффициент передачи, а – к-т затухания,
b – к-т фазы.
Область пропускания – диапазон частот, где а равно 0,
Область непропускания – диапазон частот, где а не равно 0.
Классификация фильтров в зависимости от диапазона пропускаемых частот приведена в табл. 1.
Таблица 1. Классификация фильтров
Название фильтра |
Диапазон пропускаемых частот |
|||
Низкочастотный фильтр (фильтр нижних частот) |
|
|||
Высокочастотный фильтр (фильтр верхних частот) |
|
|||
Полосовой фильтр (полосно-пропускающий фильтр) |
|
|||
Режекторный фильтр (полосно-задерживающий фильтр) |
где
|
3.2. Частотные элетрические цепи. Симметричные низкочастотные реактивные фильтры и их расчет по характеристическим параметрам.
Рассмотрим схему простейшего низкочастотного фильтра, представленную на рис. 1,а.

Связь коэффициентов четырехполюсника с параметрами элементов Т-образной схемы замещения определяется соотношениями (см. лекцию № 14)
![]()
или конкретно для фильтра на рис. 1,а
|
(2) |
|
(3) |
|
(4) |
Из уравнений четырехполюсника, записанных с использованием гиперболических функций (см. лекцию № 14), вытекает, что
![]() .
.
Однако в соответствии с (2) - вещественная переменная, а следовательно,
|
(5) |
Поскольку
в полосе пропускания частот коэффициент
затухания
![]() ,
то на основании (5)
,
то на основании (5)
![]() .
.
Так
как пределы изменения
![]() :
:
![]() ,
- то границы полосы пропускания
определяются неравенством
,
- то границы полосы пропускания
определяются неравенством
![]() ,
,
которому удовлетворяют частоты, лежащие в диапазоне
|
(6) |
Для характеристического сопротивления фильтра на основании (3) и (4) имеем
|
(7) |
Анализ
соотношения (7) показывает, что с ростом
частоты w в пределах, определяемых
неравенством (6), характеристическое
сопротивление фильтра уменьшается до
нуля, оставаясь активным. Поскольку,
при нагрузке фильтра сопротивлением,
равным характеристическому, его входное
сопротивление также будет равно
,
то, вследствие вещественности
,
можно сделать заключение, что фильтр
работает в режиме резонанса, что было
отмечено ранее. При частотах, больших
![]() ,
как это следует из (7), характеристическое
сопротивление приобретает индуктивный
характер.
,
как это следует из (7), характеристическое
сопротивление приобретает индуктивный
характер.
На
рис. 2 приведены качественные зависимости
![]() и
и
![]() .
.
Следует
отметить, что вне полосы пропускания
![]() .
Действительно, поскольку коэффициент
А – вещественный, то всегда должно
удовлетворяться равенство
.
Действительно, поскольку коэффициент
А – вещественный, то всегда должно
удовлетворяться равенство
|
(8) |
Так
как вне полосы пропускания
![]() ,
то с
,
то с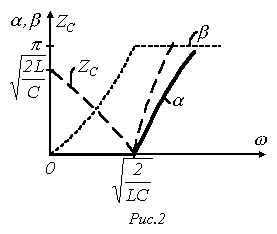 оотношение
(8) может выполняться только при
оотношение
(8) может выполняться только при
![]() .
.
В полосе задерживания коэффициент затухания определяется из уравнения (5) при . Существенным при этом является факт постепенного нарастания , т.е. в полосе затухания фильтр не является идеальным. Аналогичный вывод о неидеальности реального фильтра можно сделать и для полосы прозрачности, поскольку обеспечить практически согласованный режим работы фильтра во всей полосе прозрачности невозможно, а следовательно, в полосе пропускания коэффициент затухания будет отличен от нуля.
3.3. Частотные элетрические цепи. Высокочастотные электрические фильтры и их расчет по характеристическим параметрам.
Схема простейшего высокочастотного фильтра приведена на рис. 3,а.
Для данного фильтра коэффициенты четырехполюсника определяются выражениями
|
(9) |
|
(10) |
|
|
( |
|
Как и для рассмотренного выше случая, А – вещественная переменная. Поэтому на основании (9)
![]() .
.
Данному неравенству удовлетворяет диапазон изменения частот
|
(12) |
Характеристическое сопротивление фильтра
|
(13) |
изменяясь
в пределах от нуля до
![]() с
ростом частоты, остается вещественным.
Это соответствует, как уже отмечалось,
работе фильтра, нагруженного
характеристическим сопротивлением, в
резонансном режиме. Поскольку такое
согласование фильтра с нагрузкой во
всей полосе пропускания практически
невозможно, реально фильтр работает с
в
ограниченном диапазоне частот.
с
ростом частоты, остается вещественным.
Это соответствует, как уже отмечалось,
работе фильтра, нагруженного
характеристическим сопротивлением, в
резонансном режиме. Поскольку такое
согласование фильтра с нагрузкой во
всей полосе пропускания практически
невозможно, реально фильтр работает с
в
ограниченном диапазоне частот.
Вне области пропускания частот определяется из уравнения
|
(14) |
при
![]() .
Плавное изменение коэффициента затухания
в соответствии с (14) показывает, что в
полосе задерживания фильтр не является
идеальным.
.
Плавное изменение коэффициента затухания
в соответствии с (14) показывает, что в
полосе задерживания фильтр не является
идеальным.
Качественный вид зависимостей и для низкочастотного фильтра представлен на рис. 4.
Следует отметить, что другим примером простейшего высокочастотного фильтра может служить П-образный четырехполюсник на рис. 3,б.

 11)
11)