Периодическая система элементов

	H	He	Li	Be	B	C
2P						
2S						
1S						

Эмпирические правила Хунда:

1. Наименьшей энергией обладает состояние с наибольшим возможным значением S и наибольшем возможном при этом S значении L.

2. При этом квантовое число 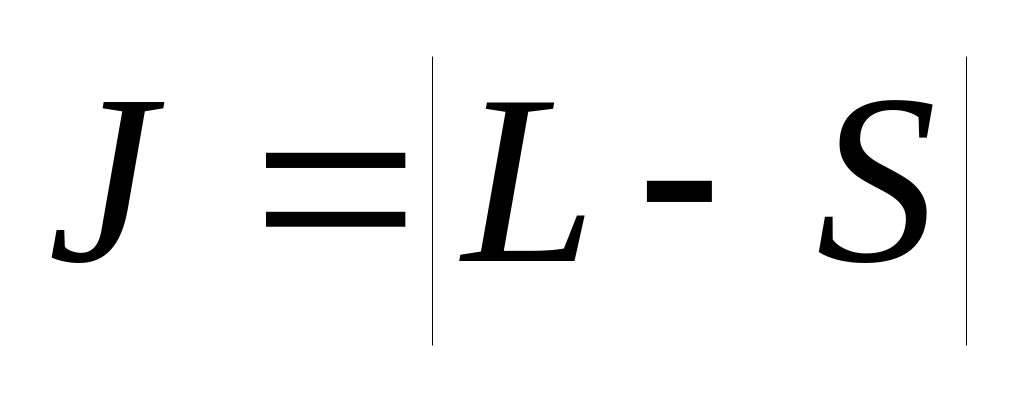, если оболочка заполнена не более, чем наполовину и 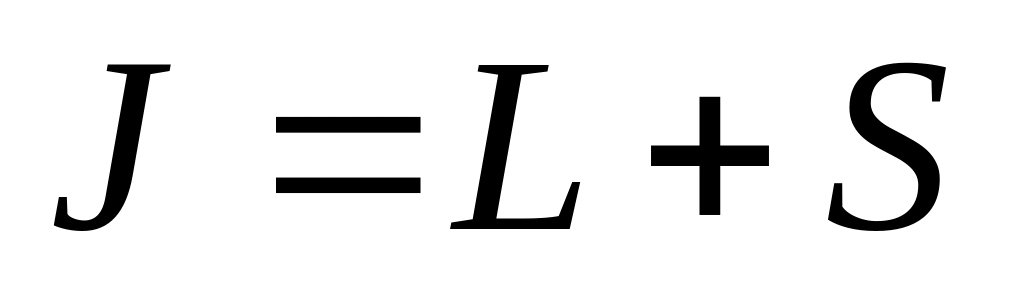во всех остальных случаях.

Рентгеновский спектр

Рентгеновского излучение можно добиться, например, таким способом:

П ри этом излучение получается, вообще говоря, сплошного спектра. Но если у налетающего электрона достаточно энергии, чтобы выбить электрон из атома вещества, образующего анод, то получается дискретный спектр, всё более ярко выраженный по мере увеличения энергии налетающих электронов. Принцип излучения таков: налетающий электрон выбивает электрон с одной из оболочек. В результате у атома появляется возможность перейти в состояние с меньшей энергией, опустив один из электронов, находящихся на верхних уровнях на освободившееся место. При этом излучается фотон с энергией , где – энергия верхнего уровня, – энергия уровня, с которого был выбит электрон. Кроме того, на освободившееся место на верхнем уровне может перейти электрон с ещё более высокого уровня.

Эмпирическое правило (закон Мозли): , где  – постоянная, разная для разных оболочек: ;  соответствует оболочке, с которой был выбит электрон. Закон Мозли модно записать в таком виде: , где R – постоянная Ридберга. Поправка возникает потому, что есть поле не одного ядра, а ещё и окружающих его электронов.

Принцип детального равновесия: Если система находится в состоянии 1 и может с какой-то вероятностью перейти в состояние 2, то она может перейти обратно с той же вероятностью.

Пусть атом находится в состоянии, характеризуемом энергией , и он облучается потоком из фотона с частотой , где – энергия другого возможного состояния атома. Пусть – вероятность того, что атом захватит один фотон. Тогда вероятность того, что он захватит фотон . Из принципа детального равновесия следует, что вероятность вернуться в исходное состояние – пропорциональна числу фотонов. Здесь член отвечает за спонтанное излучение, – за индуцированное.

Для создания лазера необходимо вещество с тремя энергетическими уровнями: основным (с наименьшей энергией), с коротким периодом жизни (т.е. с большой вероятностью распада) и метастабильным (т.е. таким, на котором атом может оставаться продолжительное время (порядка секунды)).

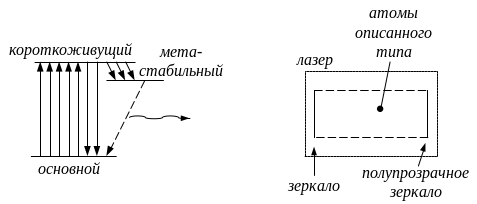
Возникший при переходе из метастабильного состояния в основное, фотон индуцирует аналогичные переходы других атомов. При этом излучаются одинаковые фотоны (обладающие одинаковыми квантовыми числами, частотой и т.д.).