Волновые свойства частиц

Утверждение де Бройля: Электрон – тоже волновая частица, как и фотон.

Частота электрона импульс волновой частицы , следовательно, длина волны электрона (волна де Бройля). Групповая скорость электрона .

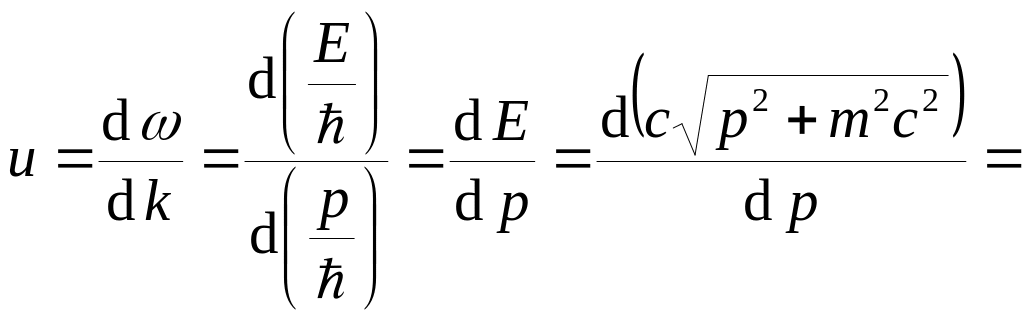
В опыте Дэвисона и Джермера поток электронов направлялся на кристалл перпендикулярно его поверхности и наблюдались максимумы под углами, соответствующими формуле Вульфа-Брэгга, если положить .

Сопоставим частице плоскую волну: .

С точки зрения волновой теории интенсивность , где A – амплитуда волны; с точки зрения корпускулярной теории , где N – количество фотонов, попадающих на приёмник в единицу времени. Вероятность нахождения частицы в объёме , где – комплексно-сопряжённая функция для .

Уравнение Шредингера

Пусть можно представить в виде: , т.е. частота, а, следовательно, и энергия колебаний, постоянна. Подставим эту функцию в волновое уравнение: . Т.к. , то . При этом , где p – импульс частицы, энергия частицы (здесь – потенциальная энергия частицы) и, следовательно, – стационарное уравнение Шредингера.

Стационарные состояния – такие состояния, которые не зависят от времени.

Принцип неопределённости Гейзенберга:

П усть электроны излучаются вдоль оси y, дифрагируют на щели и попадают на экран.

Условие минимума: . Для простоты будем считать, что максимум у интенсивности только один. Тогда электрон не будет наблюдаться, если . Разложим импульс электрона: . Тогда – интервал, в котором будет при попадании в минимум. . Ширину щели можно представить как погрешность в измерении координаты x электрона. Тогда – принцип неопределённости Гейзенберга.

Из опыта Бибермана, Фабриканта и Сушкина следует, что отдельные электроны обладают волновыми свойствами.

Итоги:

1. Микрообъекты обладают свойствами одновременно и частиц, и волн и потому не являются ни тем, ни другим в классическом смысле слова.

2. Состояния микрочастиц описываются волновыми функциями. В них свободная частица является плоской волной.

3. Микрочастицы следует представлять себе размазанными по пространству, причём 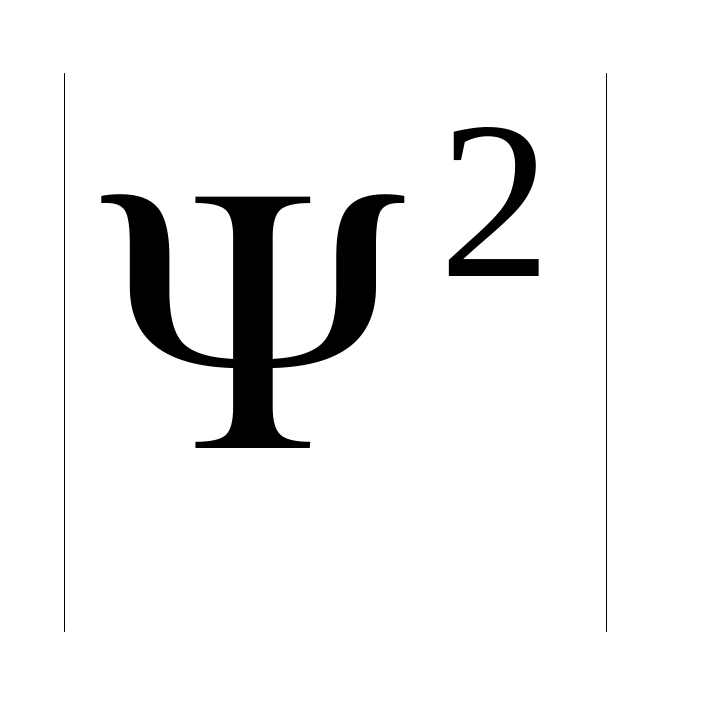характеризует плотность вероятности нахождения частицы в данном пространстве. Скорость микрочастицы совпадает с групповой скоростью волн, определяющих её состояние.

4. Микрочастицы не обладают определёнными траекториями в классическом понимании.

5. Невозможно одновременно измерить координату микрочастицы вдоль некоторой оси и проекцию импульса на эту ось. Неопределённость связана соотношением Гейзенберга: .

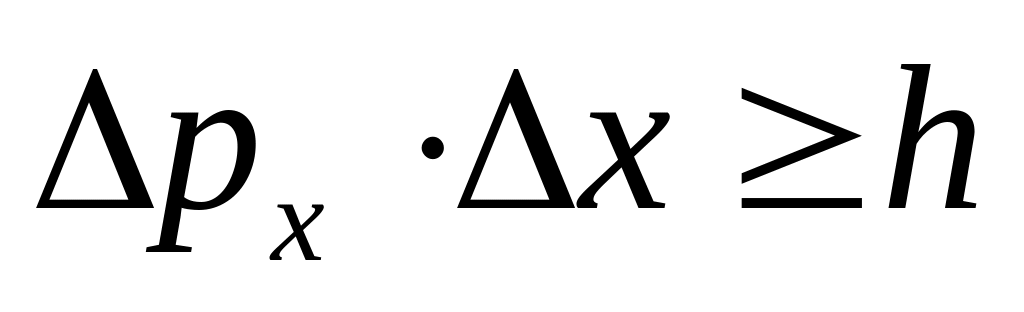6. Новое понимание опыта: произвести опыт над микрочастицей значит изменить её состояние, или -функцию.

Математические требования к -функции: непрерывность, однозначность и конечность.

Такие значения энергии, при которых  обладает требуемыми свойствами, называются собственными и функции от этих энергий тоже называются собственными.

Условие нормировки: .

Функция  определена с точностью до постоянного множителя.

Принцип суперпозиции: если частица может находится в состоянии, характеризуемом функцией и в состоянии, характеризуемом функцией , то она может находится и в состоянии, характеризуемом функцией . Пусть у частицы есть какая-то измеряемая величина L; в состоянии , в состоянии . Тогда при проведении измерения мы можем с вероятностью получить в результате , и с вероятностью – .

Оператор – это правило, которое определяет соответствие между двумя множествами функций, т.е. каждой функции из одного множества ставится в соответствие функция из другого множества. Обозначение: .

1. – линейный, если .

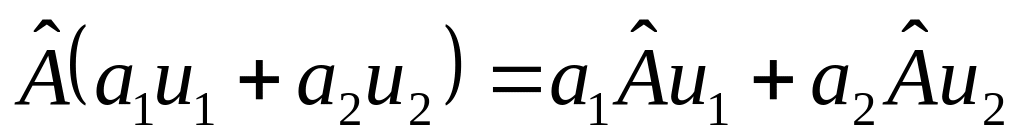2. Если 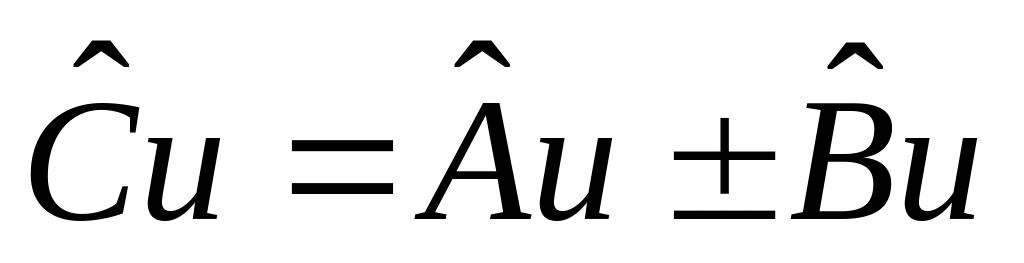, то .

3. Если , то .

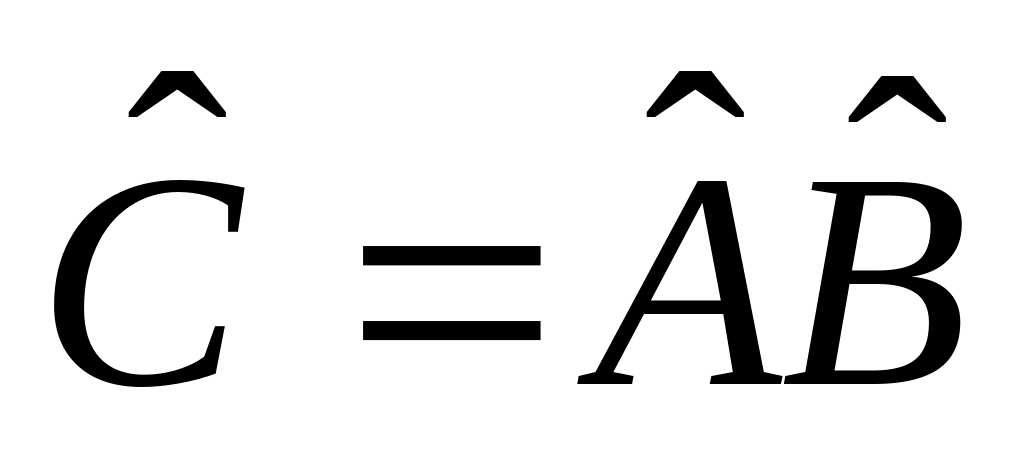4. Вообще говоря, 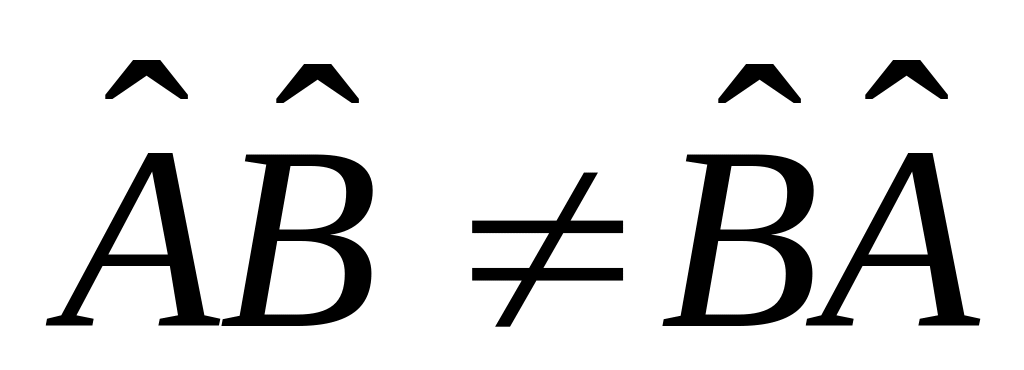. Если 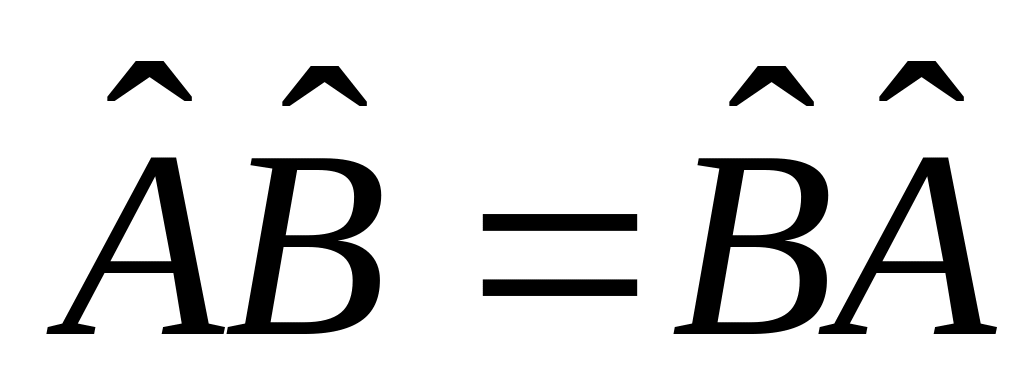, то операторы называются коммутирующими.

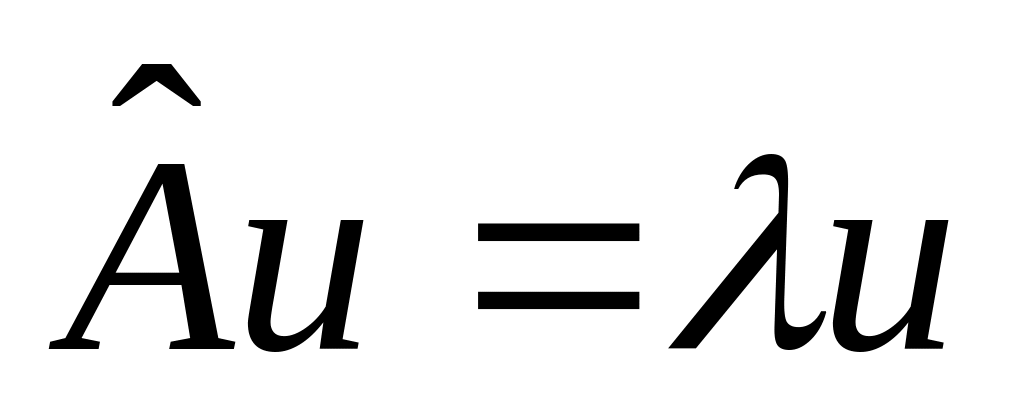5. Если , где  – число, то  называется собственным числом оператора , а u – собственной функцией оператора .

6. Если (транспонированный и комплексно-сопряжённый), то этот оператор называется самосопряжённым иди эрмитовым.

В квантовой механике используются только эрмитовые операторы.

Основные свойства эрмитовых операторов:

1. .

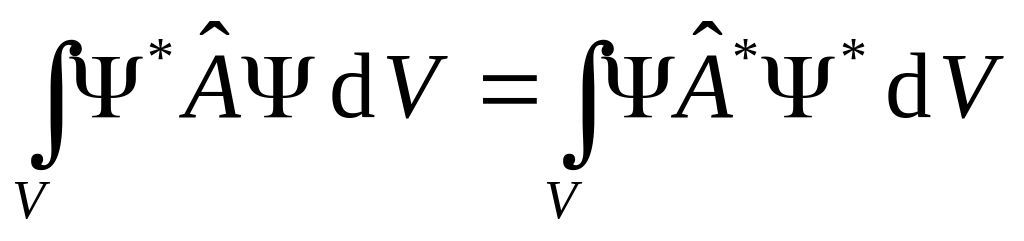2. Собственные значения эрмитового оператора – действительные числа.