Мультиплетность спектров и спин электрона

У щёлочных металлов расщепление линий перехода различно, а – одинаково.

Мультиплетность – расщепление линий на несколько компонент.

Собственный момент импульса электрона называется спином.

Квантовое число, соответствующее спину – s. Для электрона . Тогда спин электрона . Проекция спина на ось z , где для электрона. Отношение магнитного момента к механическому для электрона: . Знак «–» означает, что . .

Если в атоме один валентный электрон (атом щелочного металла), то полный магнитный момент , где через 1. Для одного электрона . Из-за того, что для уровней, у которых полный магнитный момент может принимать два значения, то и магнитный момент будет иметь два значения и состояния с различными значениями j будут обладать различной энергией.

Взаимодействие магнитных моментов электрона и атома называется спин-орбитальным взаимодействием. Им объясняется расщепление линий на две компоненты.

Правило отбора: .

Т ерм – местонахождение атома среди его энергетических уровней.

Обозначение: .

Результирующий момент многоэлектронного атома

Путём сложения всех моментов электрона, как собственных, так и орбитальных, возникает полный механический момент атома. Он получается двумя способами: если в атоме присутствует связь Ресселя-Сандерса, то взаимодействие собственных магнитных моментов и взаимодействие орбитальных моментов электронов сильнее, чем взаимодействие собственных и орбитальных моментов электронов. Тогда , где N – число электронов, и – соответственно орбитальный и собственный моменты i-го электрона. Иначе в атоме присутствует j-j-связь. Тогда . Эта связь встречается реже и свойственна тяжёлым атомам.

Можно представить так: , где g – фактор Ланде, зависящей от L и S.

С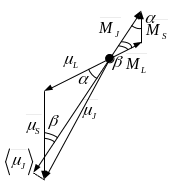 реднее по времени значение полного магнитного момента . При этом . Аналогично . Тогда .

Распределение электронов в атоме по энергетическим уровням

Принцип Паули: В одной и той же квантовой системе не может быть двух частиц с полуцелым спином, обладающих одним и тем же набором квантовых чисел.

Состояние электронов в атоме характеризуется числами: .

Основным состоянием атома является такое, которое обладает минимальной энергией.

Вырождение по числу для электрона равно . При – 2 электрона, .

Совокупность электронов, характеризующихся одинаковым главным квантовым числом, называется слоем.

Совокупность электронов, характеризующихся одинаковым орбитальным квантовым числом, называется оболочкой.

Иногда слои называют оболочками, а оболочки – подоболочками.

Слой	Оболочка	n	l
К		1	0	0	
L	2S	2	0	0	
	2P		1	–1	
				0	
				1	
M	3S	3	0	0	
	3P		1	–1	
				0	
				1	
	3D		2	–2	
				–1	
				0	
				1	
				2	

Для полностью заполненной оболочки суммарный орбитальный момент равен 0 и суммарный спиновой момент равен 0, следовательно, и полный механический момент равен 0.