§4 Метод последовательного исключения неизвестных.(Метод Гаусса).

Пусть дана система уравнений с неизвестными:

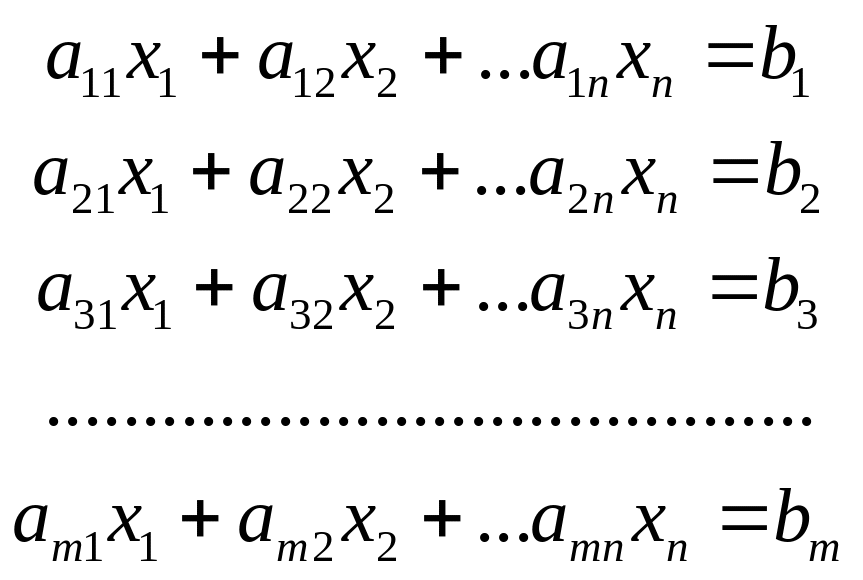(1)

М етод Гаусса состоит в следующем. Предполагая, что (уравнения всегда можно переставить), умножая первое уравнение и прибавляя ко второму, получим уравнение, в котором коэффициент при обращается в 0. Затем, умножая первое уравнение на и прибавляя к третьему, получаем уравнение так же не содержащее члена с . И так далее, аналогичным путем преобразуем остальные уравнения, в результате чего система (1) примет вид:

(2)

где - новые коэффициенты.

Предполагая, что , оставляя неизвестными первые два уравнения системы (2), преобразуем ее так чтобы в остальных уравнениях с по коэффициент при обратился в 0. Продолжая этот процесс, систему можно привести к одной из следующих систем:

случай:

(3)

, где , и - новые коэффициенты, после преобразований.

Система (3) имеет единственное решение, значение находим из последнего уравнения, значение - из последнего и т.д. значение из первого.

Это случай теоремы 1 из §3.

Случай 2^й.

Если , то:

(4)

В системе (4) уравнения с до полностью нулевые. Эта система имеет бесконечное множество решений. Из которого уравнения выразить через , из уравнения можно выразить через и т.д. в полученных формулах, выражающих , через , неизвестные могут принимать любые значения. Это случай теоремы 2 из §3.

Случай 3^й: .

(5)

В системе (5) в уравнениях с по коэффициенты при неизвестных равны 0, а свободные члены отличны от 0. Система (5) не совместна, т.к. никакие значения переменных не могут удовлетворять уравнениям с по -е. (т.е. , по теореме Кронекера-Капелли система не совместна).

Замечание:

Решая систему этим методом, преобразования совершают не над уравнениями, а над расширенной матрицей системы, тем самым находя одновременно ранг основной матрицы системы и ранг расширенной матрицы системы.

П ример 1:

=

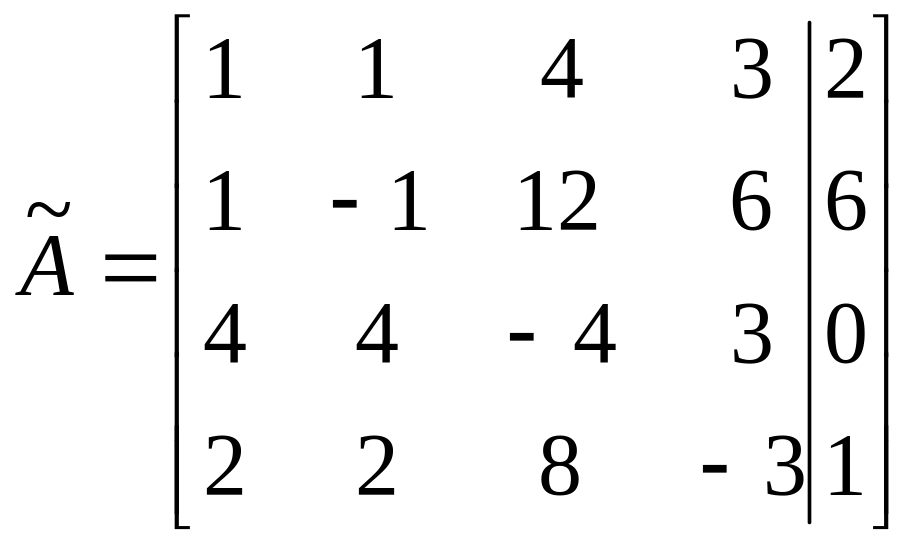
Это 1 случай Гаусса и теоремы 1 из §3.(т.к. очевидно что ).

Решая уравнения от последнего к первому получаем единственное решение:

.

Пример 2:

Иллюстрация 2^го случая Гаусса и теоремы 2 §3.

Пример 3.

.

= =

= .

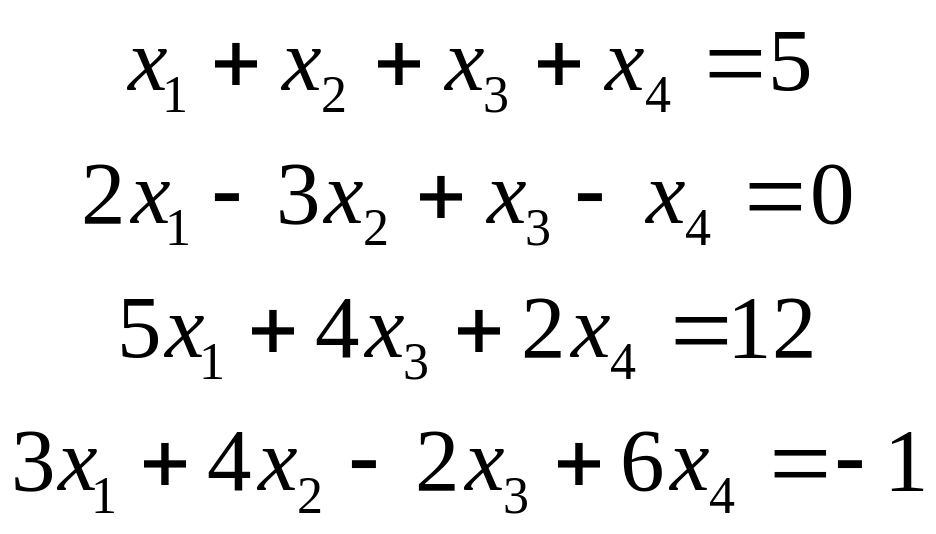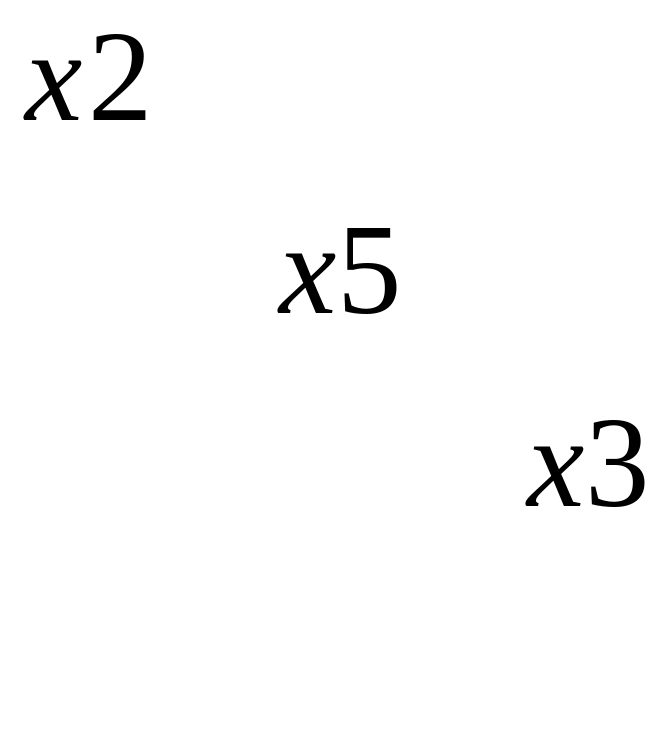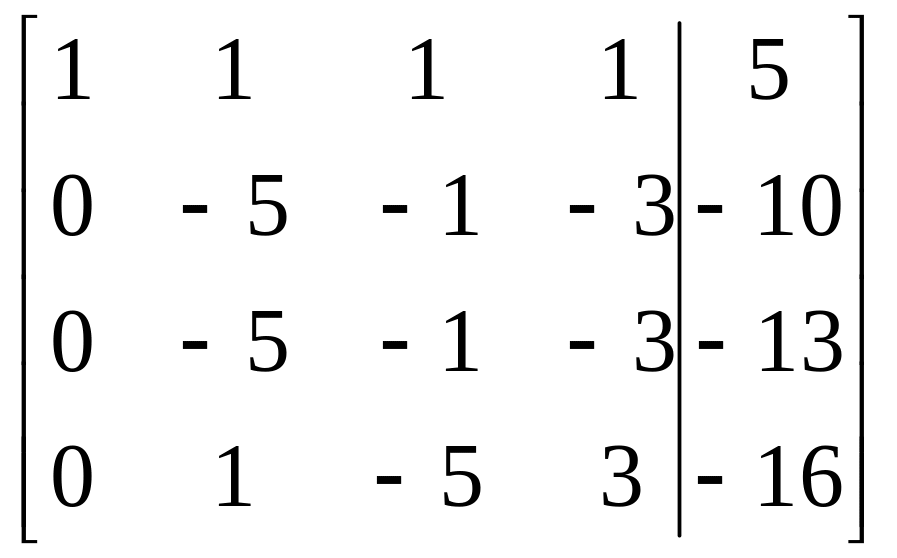Это третий случай метода Гаусса. В третьей строке все коэффициенты нулевые, а свободный член 0. Значит система не совместна.

С другой стороны.

. .

.

.

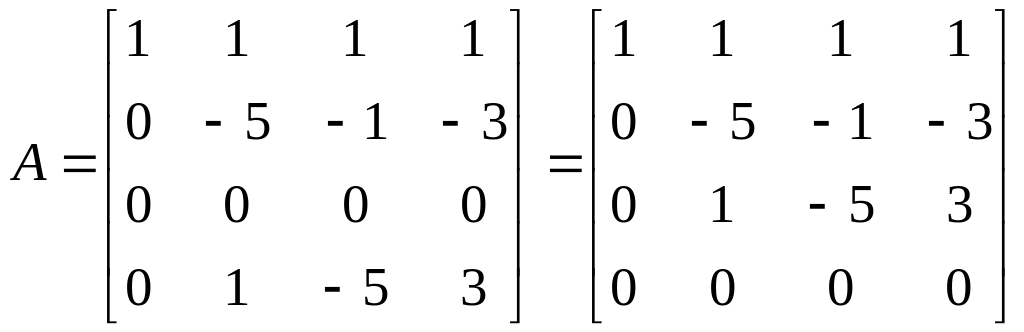
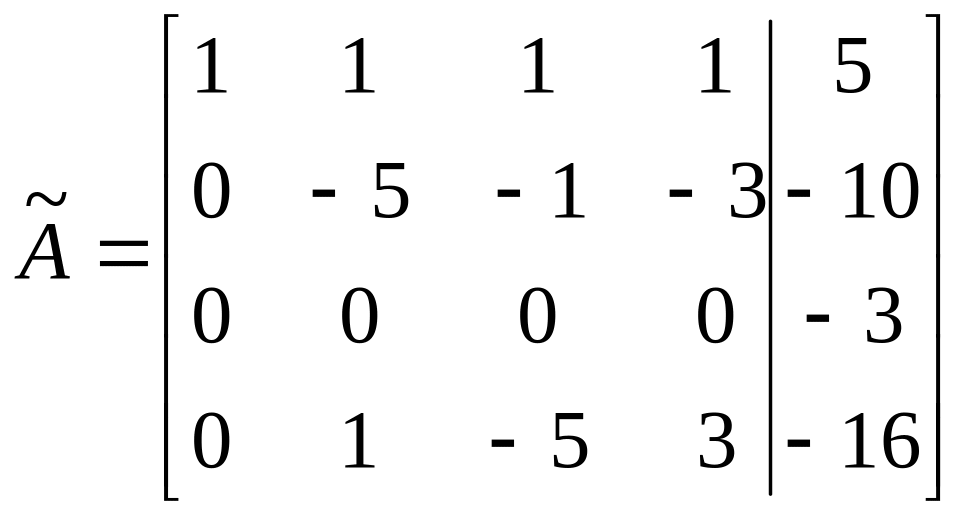
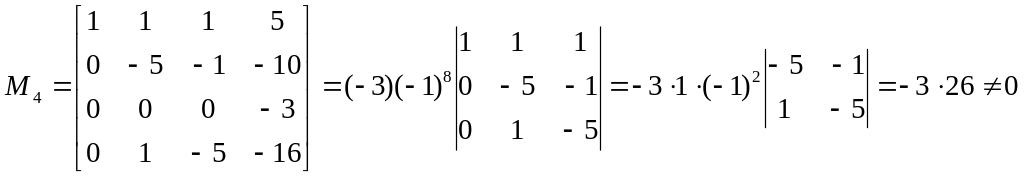, по Кронекера-Капелли система так же не совместна.