§ 3. Исследование систем линейных уравнений.

Пусть дана система уравнений с неизвестными:

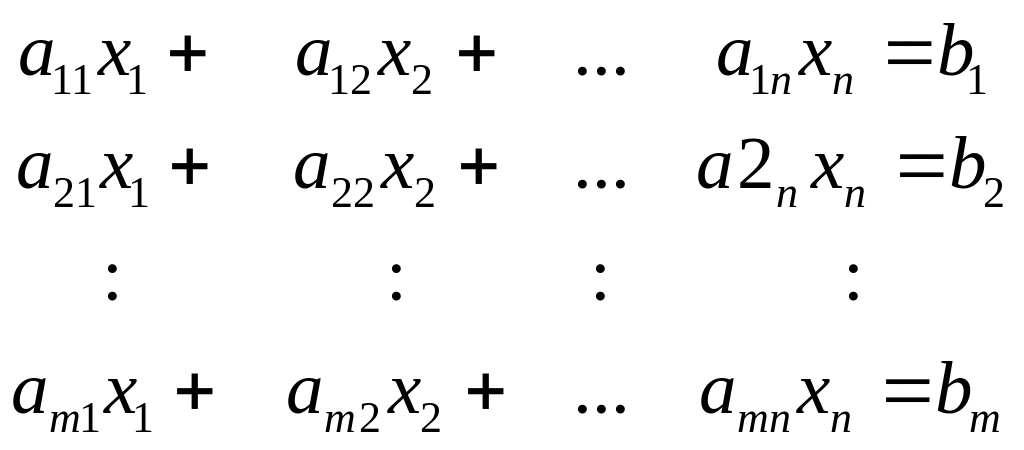(1)

Система (1) может быть записана в виде матричного уравнения , а матричное уравнение в форме:

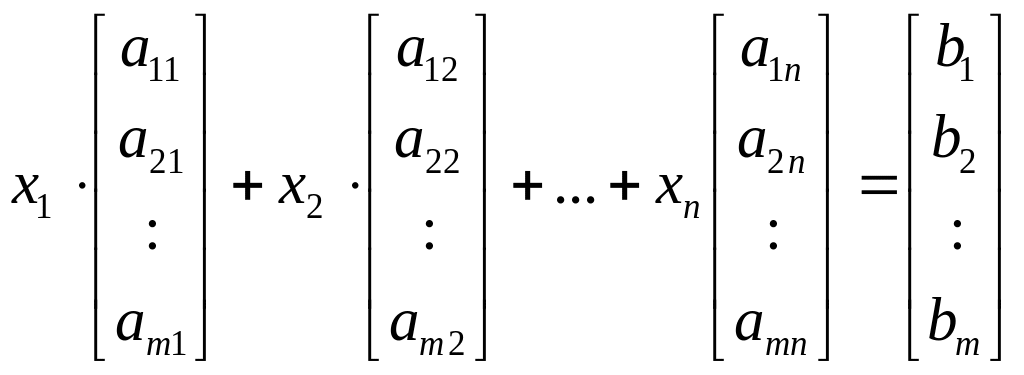(2)

Легко проверить, используя определения умножения матриц на число и сложение матриц.

Рассмотрим матрицу системы и расширенную матрицу системы .

.

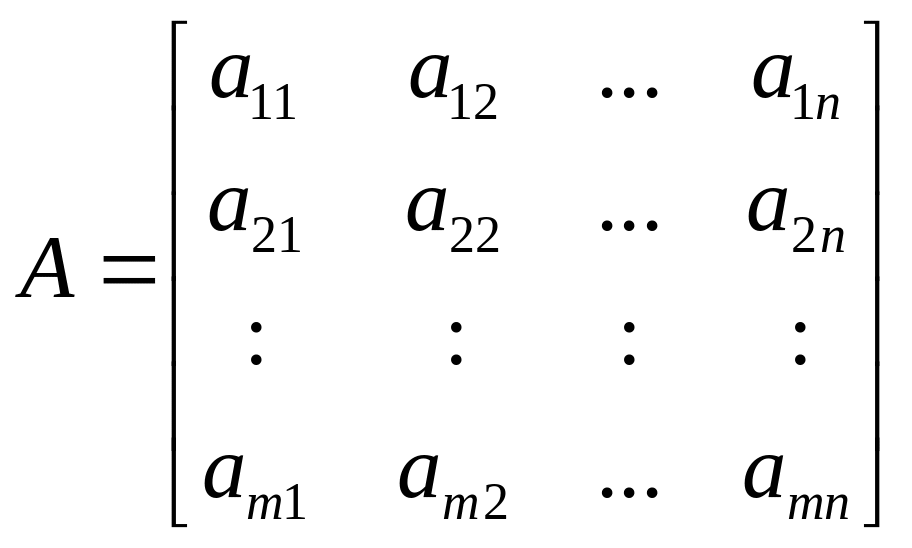
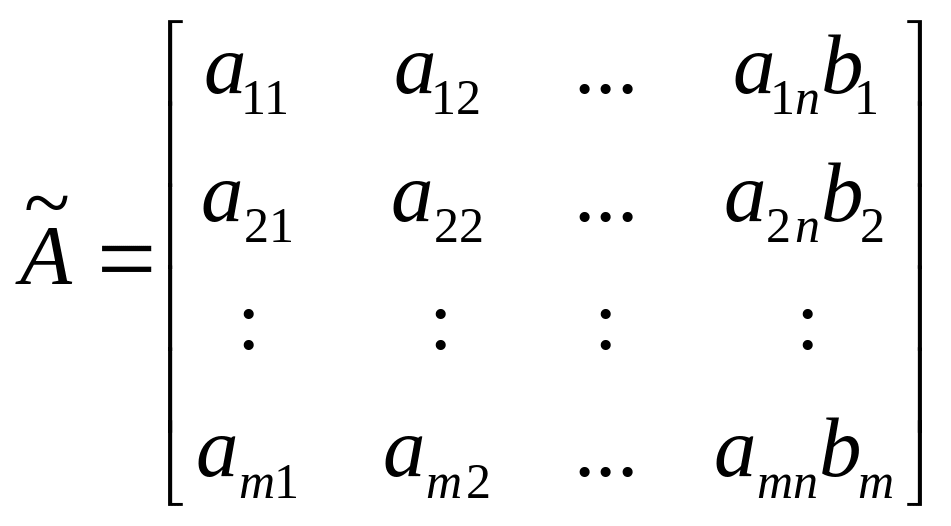Теорема Кронекера-Капели.

Для того чтобы система линейных алгебраических уравнений была совместной, необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу ее расширенной матрицы.

Доказательство (необходимость):

Пусть система (1) совместна , требуется доказать, что ранг равен рангу .

Если система (1) совместна, то она имеет решение. Пусть совокупность чисел есть решение системы, которые при подстановке в систему (2) вместо неизвестных обращает уравнение в верное равенство:

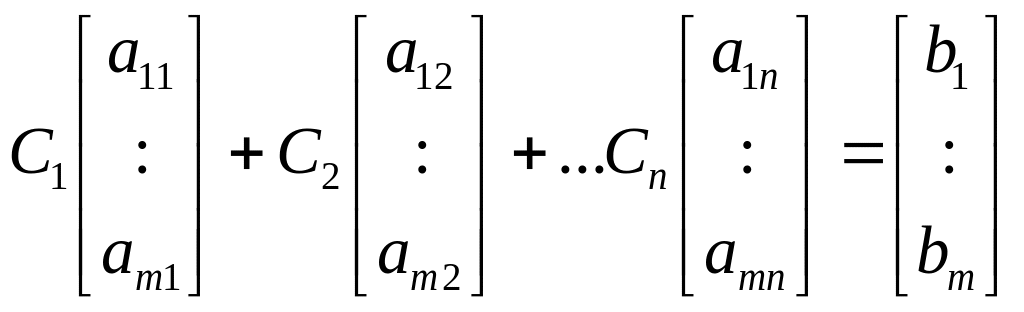(3)

Из (3) следует, что последний столбец расширенной матрицы - есть линейная комбинация остальных ее столбцов. Следовательно, путем линейных преобразований над столбцами матрицы , ее можно привести к виду:

.

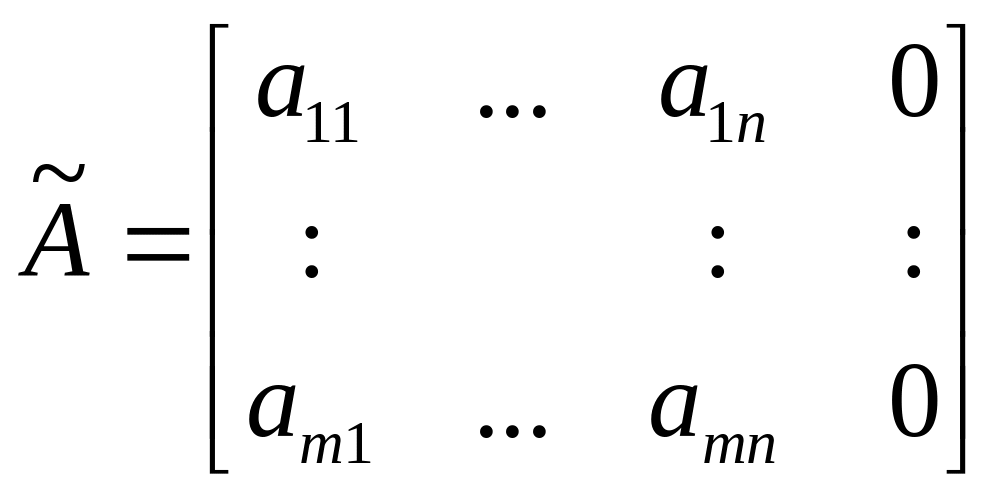Отсюда видно, что .

Доказательство (достаточность):

Требуется доказать, что система (1) совместна. Так как , то существует минор , который является базисным как для матрицы так и для . Так как последний столбец свободных членов входит только в , то в общий базисный минор последний столбец не может входить, значит он является линейной комбинацией базисных столбцов, входящих в минор. А следовательно столбцов матрицы . Значит существуют такие числа отличные от нуля, что имеет смысл равенство:

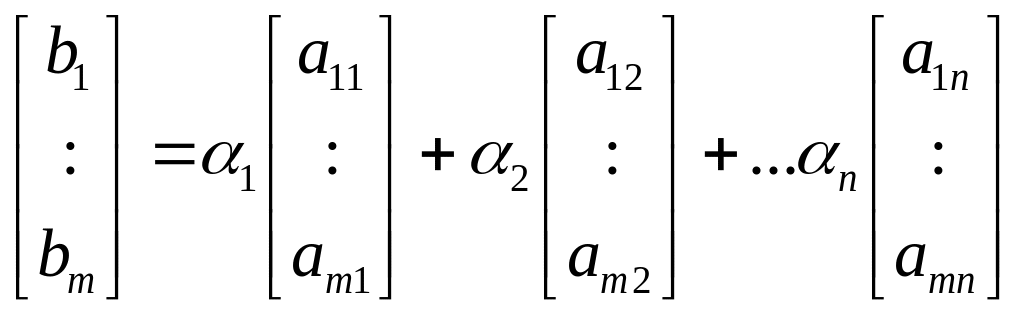(4)

^{линейная комбинация базисных столбцов А.}

Сравнивая (4) и (3), получаем, что числа - есть решение системы (1).

Значит, (1) совместна.

Теорема 1.

Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение.

Напомним, что базисным минором матрицы называется отличный от нуля ее минор, порядок которого равен рангу этой матрицы. Базисными неизвестными совместной системы, ранг матрицы которой равен , назовем неизвестных, коэффициенты при которых образуют базисный минор. Остальные неизвестные назовем свободными.

Таким образом в случае теоремы 1, число базисных неизвестных равно числу неизвестных системы, тогда система имеет единственное решение, которое можно найти по формуле Крамера.

Теорема 2.

Если ранг матрицы совместной системы меньше числа неизвестных, то множество решений системы является бесконечным, т.е. система не определена.

Т.о. в случаях теоремы 2,число базисных неизвестных r меньше числа всех неизвестных. Тогда от системы (1) переходят к эквивалентной системе, которая получена следующим образом:

1. Сохраним в системе r уравнений, соответствующих базисному минору.

Остальные уравнения отбрасываем.

2. В сохраненных уравнениях в левой части оставляем базисные неизвестные, свободные неизвестные переносим в право.

Если предположим, что базисный минор M располагается в левом верхнем углу матрицы системы, ранг матрицы равен r, тогда неизвестные - базисные, а неизвестные - свободные и система примет вид:

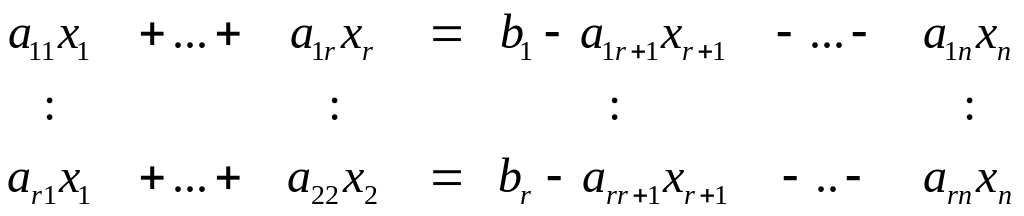(5)

Присвоим неизвестным свободным произвольные значения:

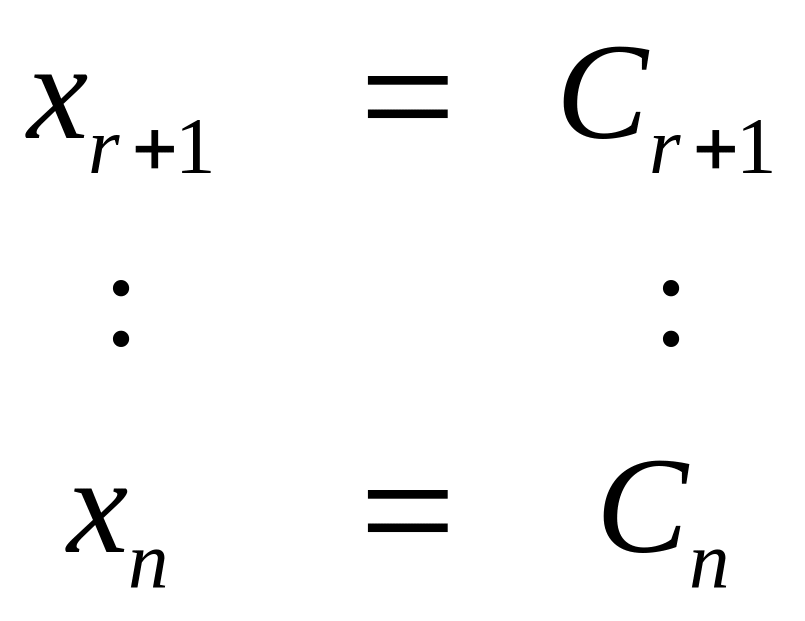
Тогда система (5) примет вид:

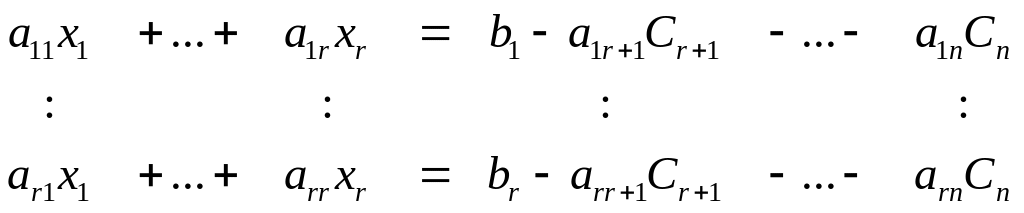(6)

Система (6) имеет единственное решение, так как ее определитель .

Решая (6) по формулам Крамера получим неизвестные , которые будут выражены через константы .

Решение примет вид:

.

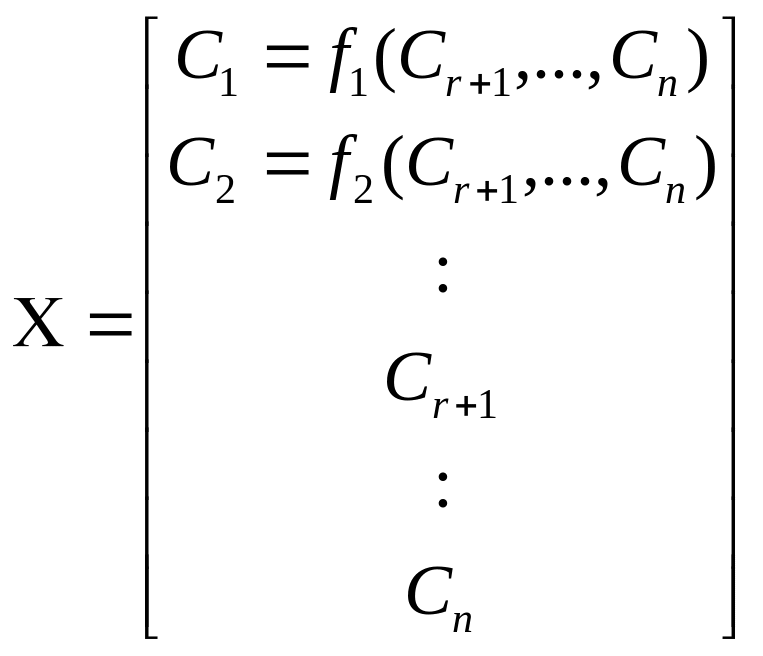План решения системы линейных алгебраических уравнений:

1. Найти ранг матрицы системы, и ранг расширенной матрицы системы. Если 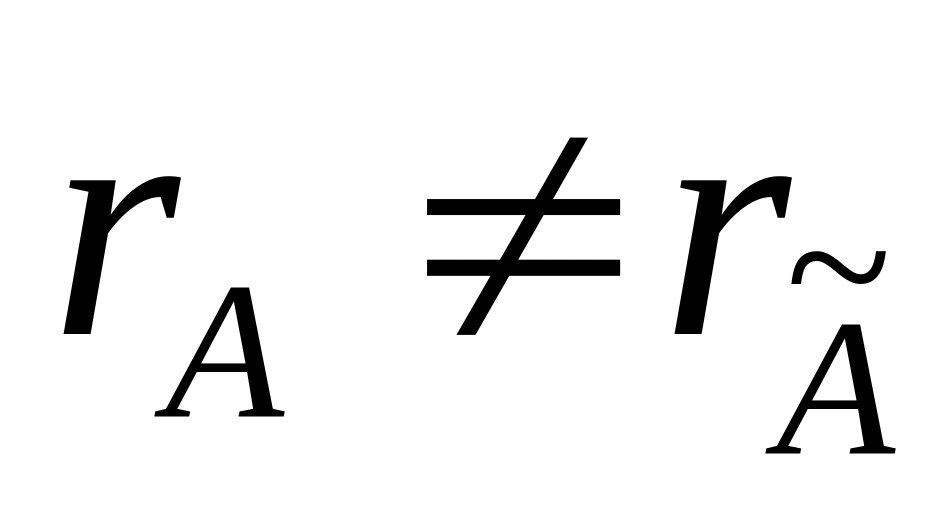, то система не совместна.

2. Если , то система совместна, выбрать базисный минор и базисные переменные.

3. Перенести свободные неизвестные в правую часть и решать систему относительно базисных неизвестных.

4. Если число базисных неизвестных равно числу всех неизвестных системы, т.е. если свободных неизвестных нет. То система имеет единственное решение.

5. Если число базисных неизвестных меньше числа всех неизвестных системы, то система имеет множество решений причем базисные неизвестные выражаются через свободные.

Пример 1.

Решить систему:

= =

= = =

.

.

. .

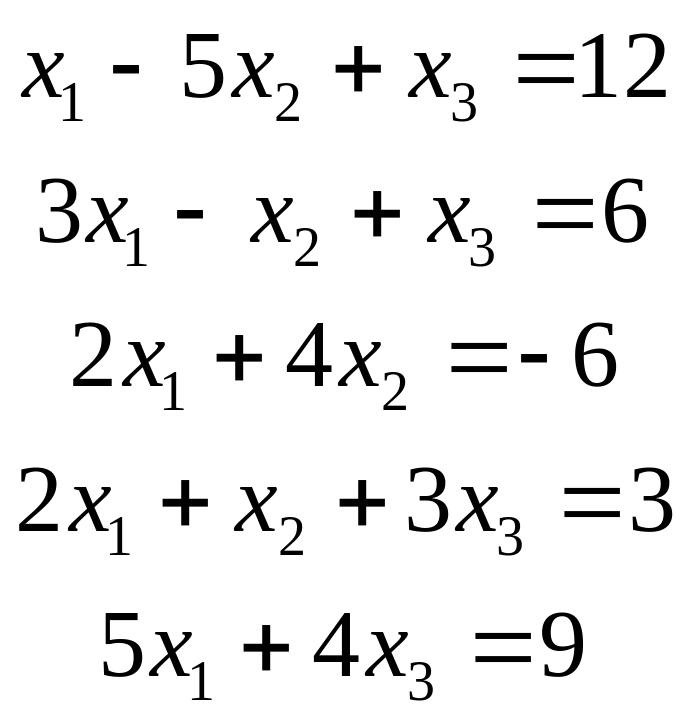
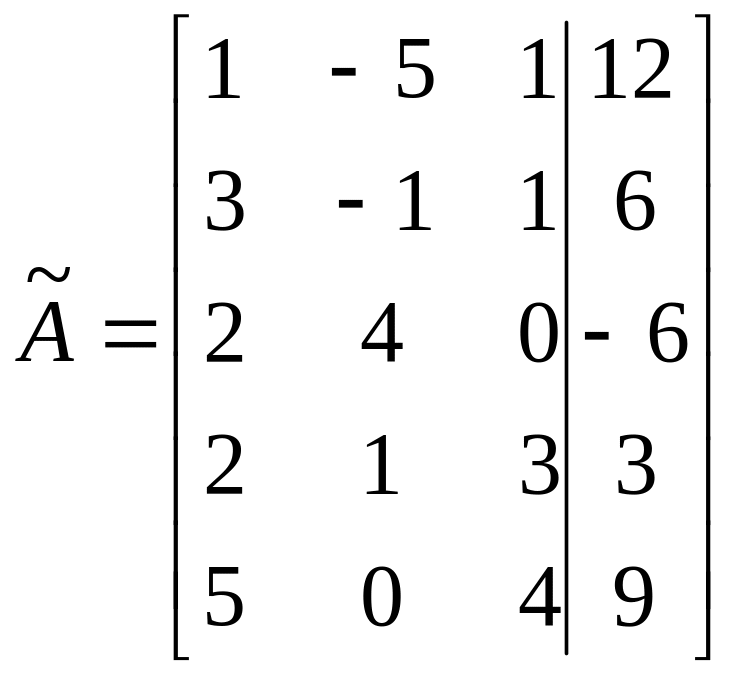
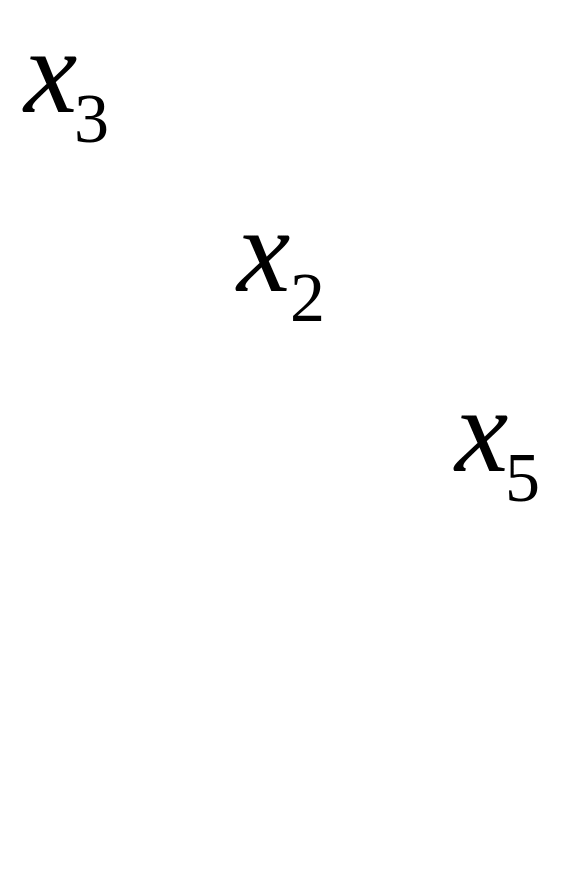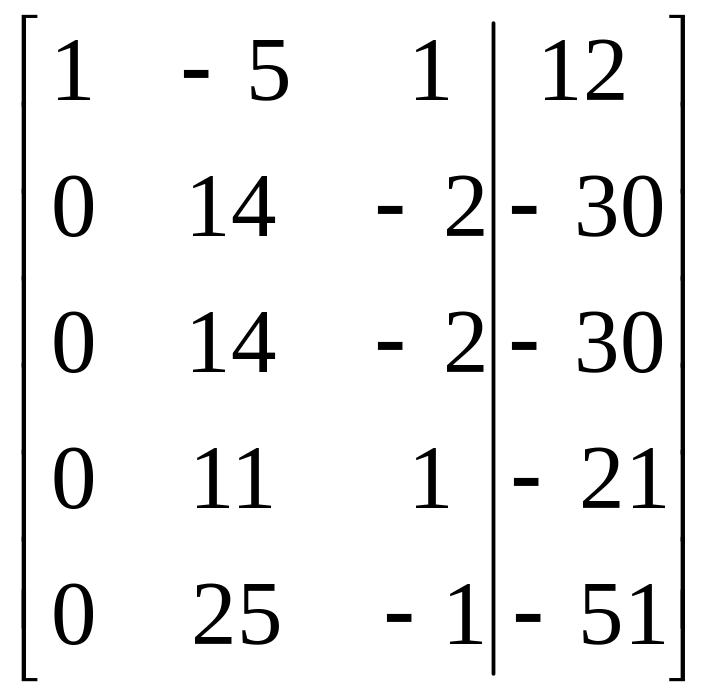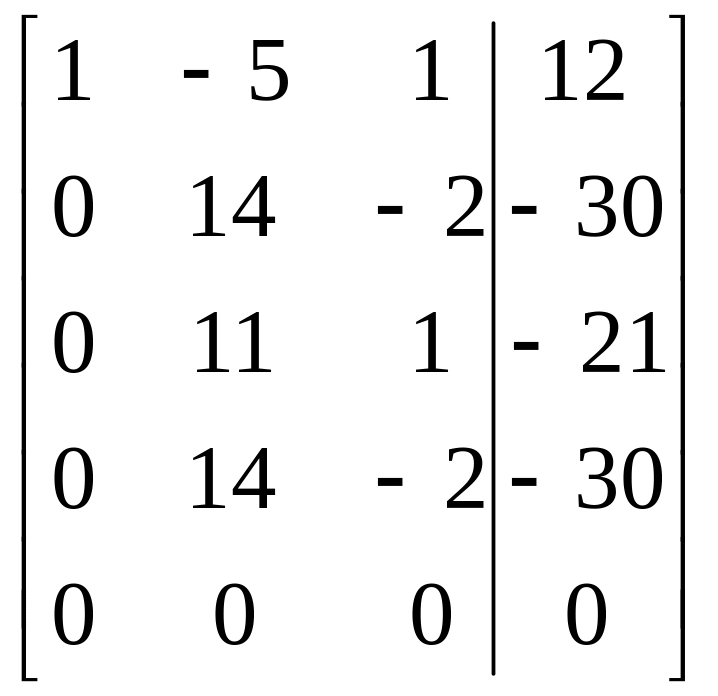
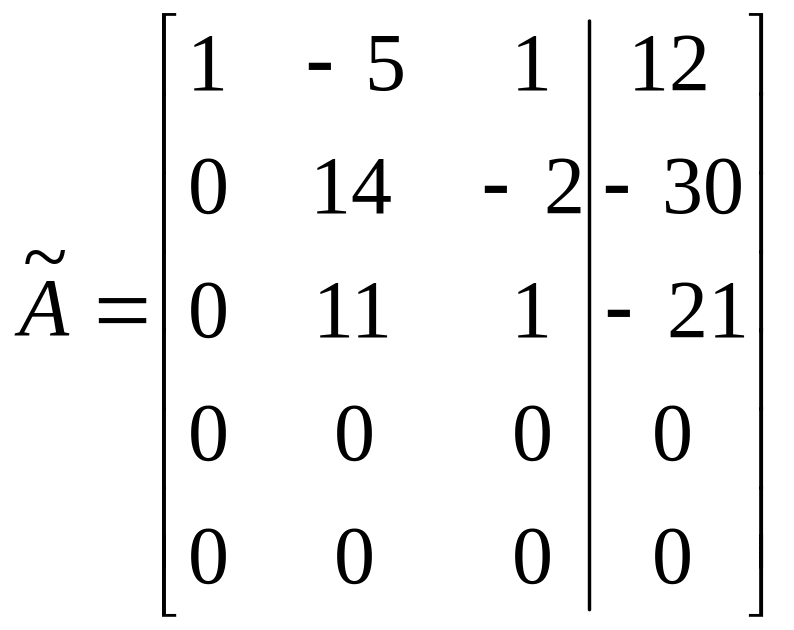
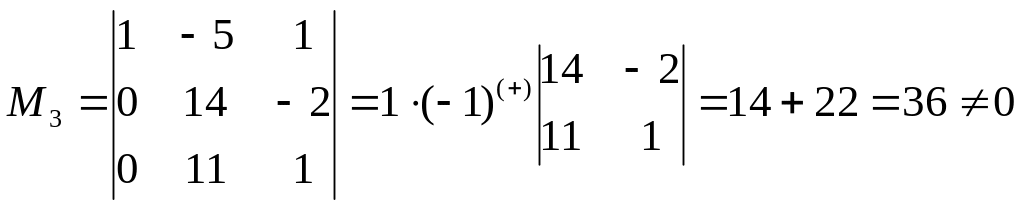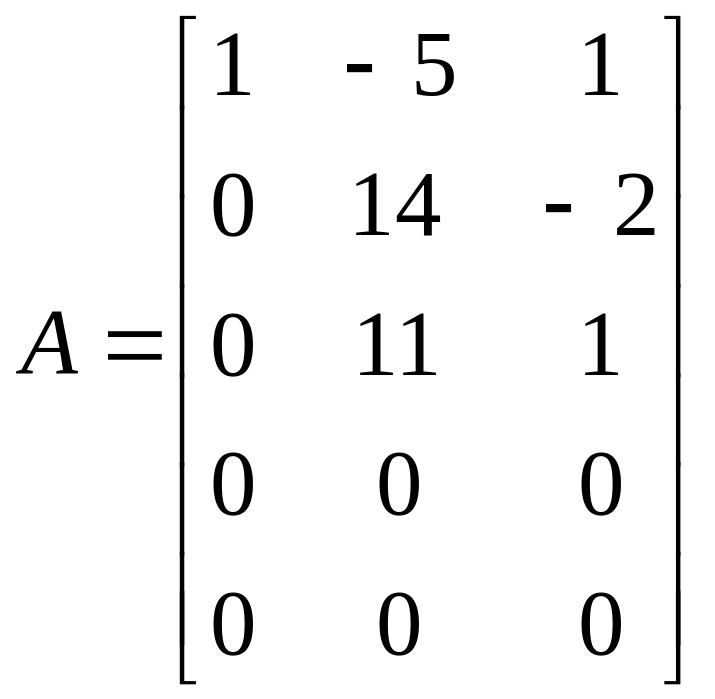
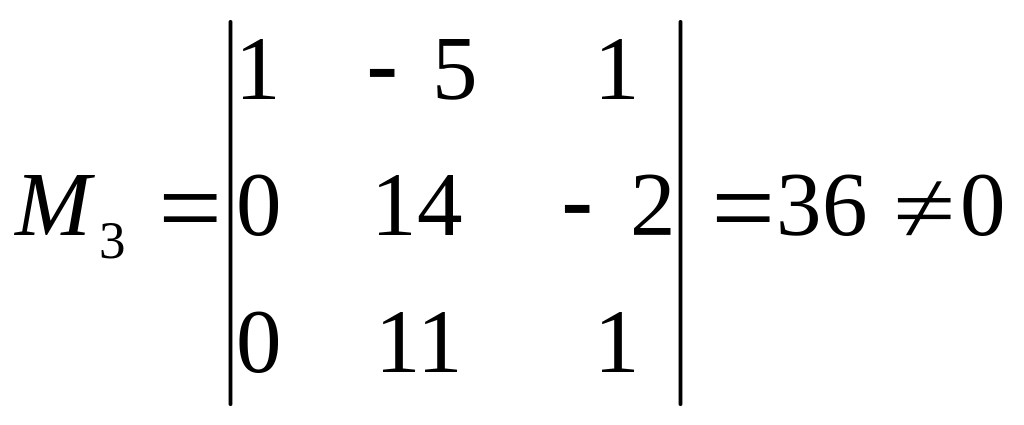- система совместна.

Эквивалентная система (на миноре );

Число неизвестных равно рангу 3, система имеет единственное решение.

Базисные переменные . Свободных переменных нет.

(случай теоремы 1)

Определитель системы , решая систему по формулам Крамера- получаем единственное решение:

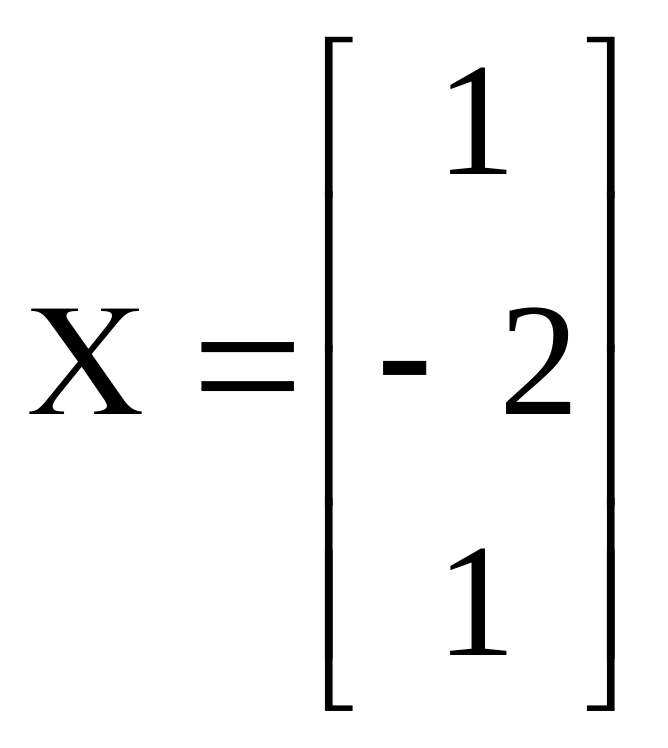
Пример 2.

=

= = .

. .

. .

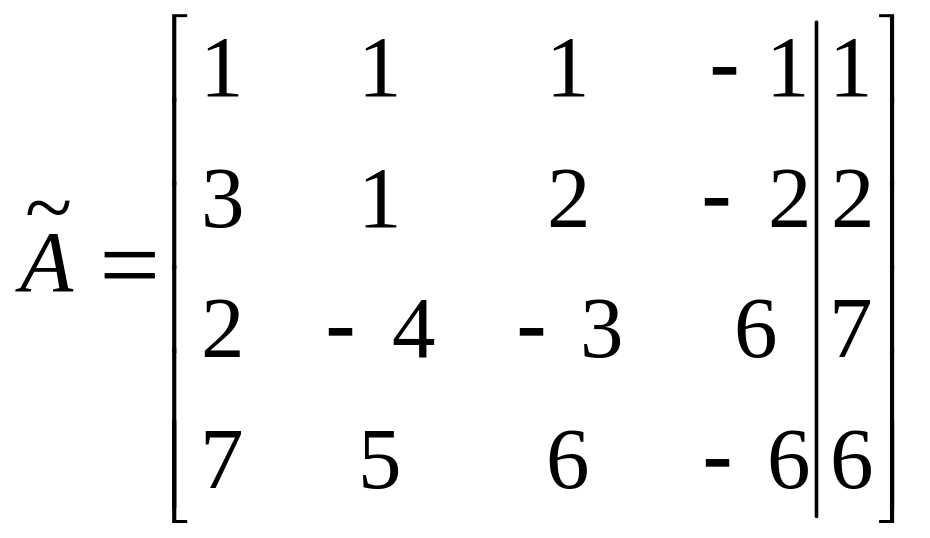
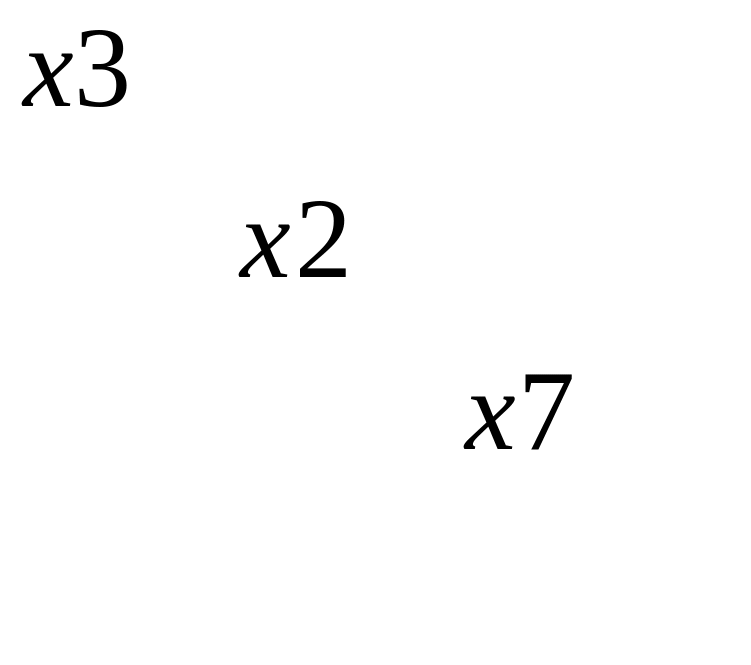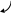
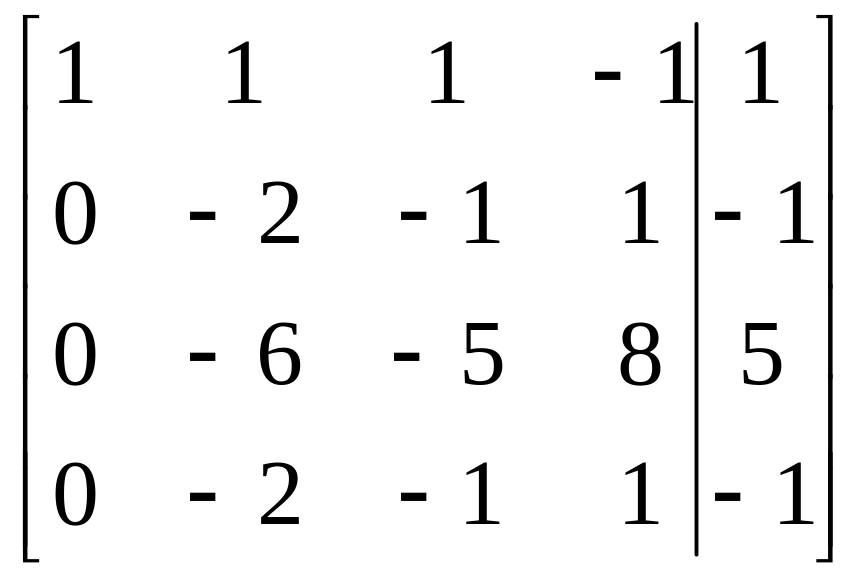
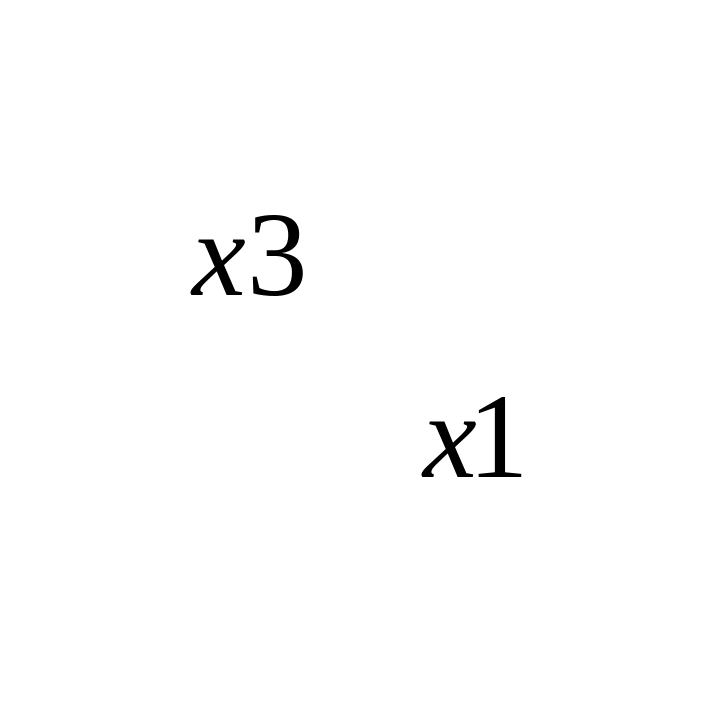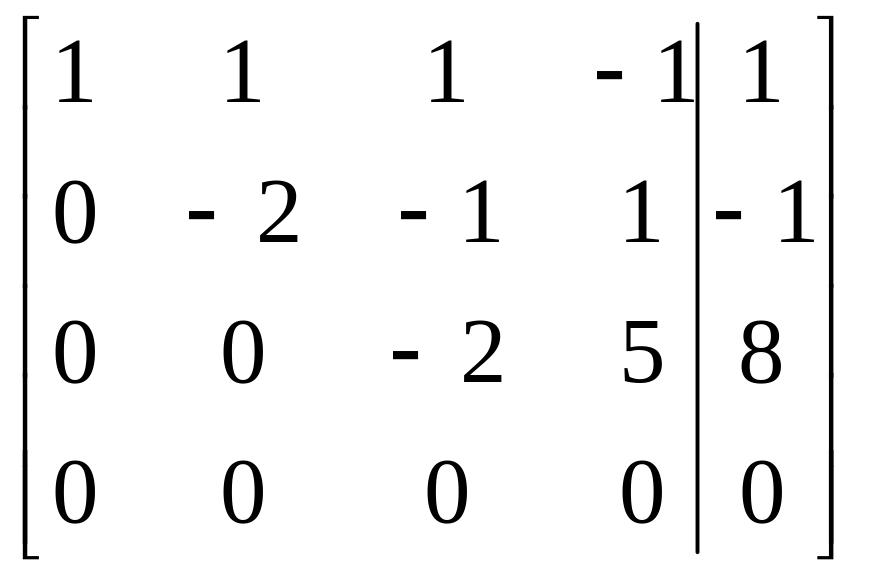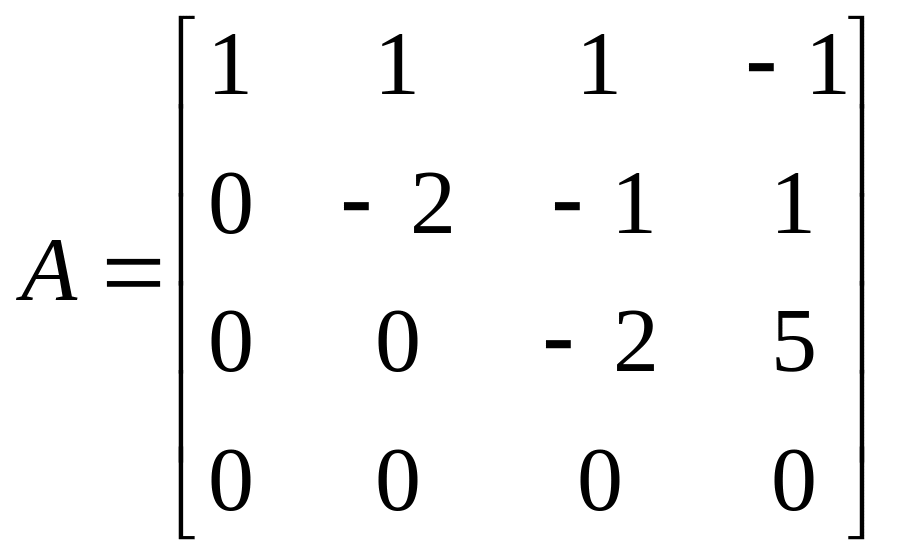
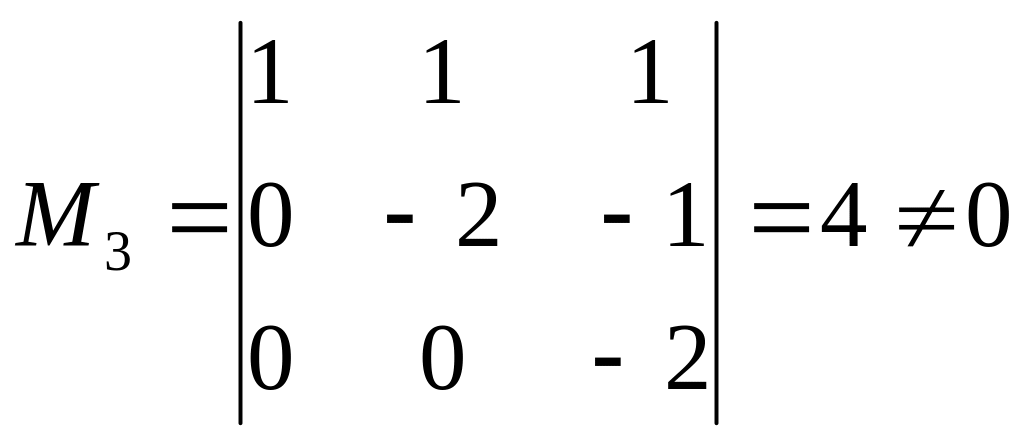- система совместна. Ранг 3 меньше числа неизвестных 4, система имеет бесконечное множество решений (случай теоремы 2). Записываем эквивалентную систему на базисном миноре:

. Коэффициенты входят в - эти неизвестные базисные,

. - свободное неизвестное.

.

Пусть  .

.

.

Определитель данной системы , ее можно решить формулами Крамера или последовательно выражая через . Ответ будет иметь вид:

.