§8. Смешанное произведение трех векторов.

Определение: Смешанным (векторно-скалярным) произведением упорядочнной тройки векторов и называется число равное скалярному произведению вектора на третий вектор .

Обозначают , , .

Геометрические свойства произведения трех векторов:

h

S

1⁰. Объем параллелепипеда построенного на векторах , и равен модулю смешанного

произведения этих векторов.

+V, если - правая тройка.

-V, если - левая тройка.

2⁰. Необходимое и достаточное условие компланарности векторов.

- компланарны, значит линейно зависимы, и не образуют базиса.

- не компланарны, линейно не зависимы и не образуют базис.

3⁰. Если , то - правая тройка.

Если , то -левая тройка.

Алгебраические свойства смешанного произведения:

1⁰. Смешанное произведение не изменится если знаки векторного и скалярного умножения

поменять местами:

.

2⁰. Смешанное произведение не изменится от круговой перестановки множителей:

.

3⁰. .

4⁰. .

5⁰. .

Смешанное произведение в прямоугольных координатах.

Пусть даны три вектора:

, тогда:

.

Следствие 1:

.

B

h C

S

A D

Следствие 2: Условием того, что четыре точки лежат в одной плоскости является равенство 0

смешанного произведения:

B

.

A. C

D

Пример 1. В прямоугольном базисе дана треугольная пирамида с вершинами в точках: A(3,5,4),

B (8,7,4), C (5,10,4), D (4,7,8).

Найти длину высоты проведенной из вершины D на грань (ABC).

D

A. B

C

.

.

.

.
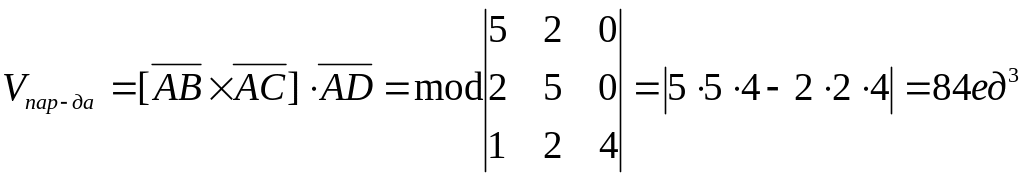
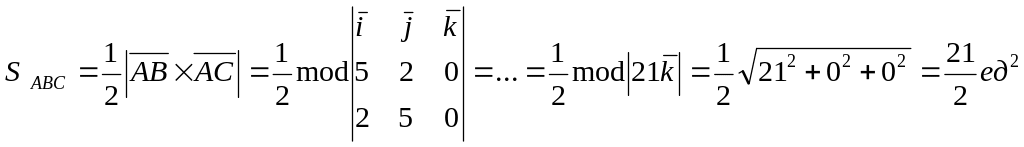