§6 Скалярное произведение двух векторов.
Скалярным
произведением,
двух ненулевых векторов
и
называют
число равное произведению длин этих
векторов на косинус угла между ними и
обозначают
либо
.
.
0
φ
Если хотя бы один из векторов нулевой, то скалярное произведение.
Из
def
;
.
Геометрические свойства скалярного произведения:
10. Скалярный квадрат вектора равен квадрату его длинны.
20.
Если
,
т.е.
.
Необходимым и достаточным условием перпендикулярности векторов является равенство 0 их скалярного произведения.
30.
Если
,
то
,
т.е. угол
-
острый.
Если
,
то
,
угол тупой.
Замечание: Из геометрических свойств - следует.
,в
силу их перпендикулярности.
Алгебраические свойства скалярного произведения.
10.
20.
,
где
Q
<
–используется def
скалярного
произведения,
свойство проекции.
30.
<
>
Механический смысл скалярного произведения. Работа постоянной силы, есть число равное скалярному произведению вектора силы и вектора перемещения .
Скалярное произведение в полярных координатах.
Пусть даны два вектора ; .
( остальные слагаемые равны 0, т.к. i j k , смотри геометрические свойства).
.
Скалярное произведение двух векторов в прямоугольном базисе равно сумме произведений одноименных координат (Если в плоскости, то отсутствует z1z2)
Следствие
1:
По определению
,
где
Следствие
2:
Следствие
3:
.
Пример
1:
Дано:
;
,
в
прямоугольном базисе.
Найти: .
.
.
Пример
2:
Дано:
,
,
-
в произвольном
базисе.
Найти:
Решение:
.
§7 Векторное произведение двух векторов.
Определение:
Векторным
произведением двух векторов
и
называют
вектор обозначаемый
[
]
или
такой,
что:
10. Длина вектора равна произведению длин векторов и на sin угла между ними.
20. Вектор перпендикулярен к обоим векторам и .
30.
Вектор
направлен
так, что
упорядоченная
тройка векторов
образует
правую тройку.
0
(Упорядоченная тройка векторов называется правой, если с конца третьего вектора кратчайший поворот от первого до второго происходит против часовой стрелки (если по часовой стрелке, то тройка левая)).
Геометрические свойства векторного произведения.
10. Модуль векторного произведения равен площади параллелограмма построенного на этих векторах и :
S
0
20. Если вектора и коллинеарные, то их векторное произведение равно 0.
Если
,
,
то
,
.
В частности, векторное произведение вектора а самого на себя так же равно 0.
30. Векторное произведение перпендикулярно плоскости, в которой лежат и .
Алгебраические свойства векторного произведения.
10. [ , ] =- [ , ] – анти коммутативное.
20.
30.
Механический смысл векторного произведения.
Момент
силы
приложенной
к точке В
относительно
точки 0
(начало
координат) есть вектор равный
.
z
0
y
x
B
Векторное произведение в прямоугольных координатах.
И
з
геометрического свойства следует:
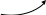0
Пусть заданы два вектора:
и
Тогда
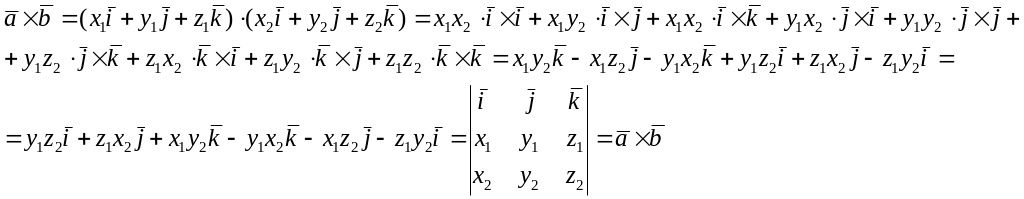
Следствие. Площадь параллелограмма равна модулю векторного произведения, векторов на которых он основан.
b
h
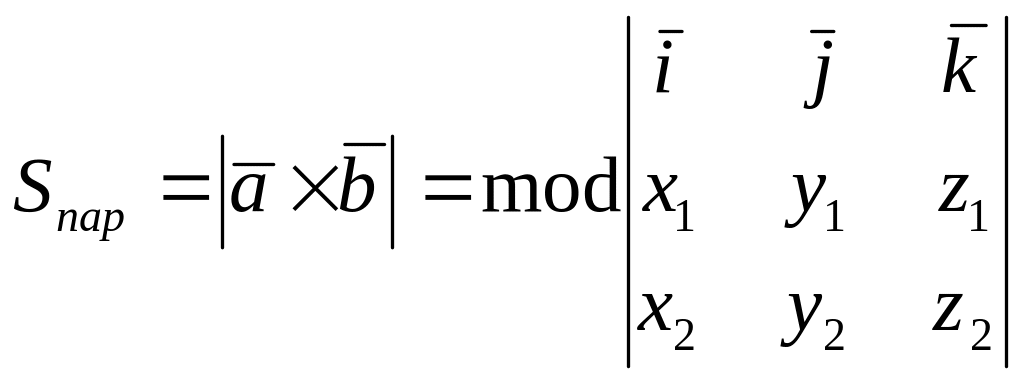
a
.
Пример
1.Вычислить
высоту параллелограмма, построенного
на
.
.
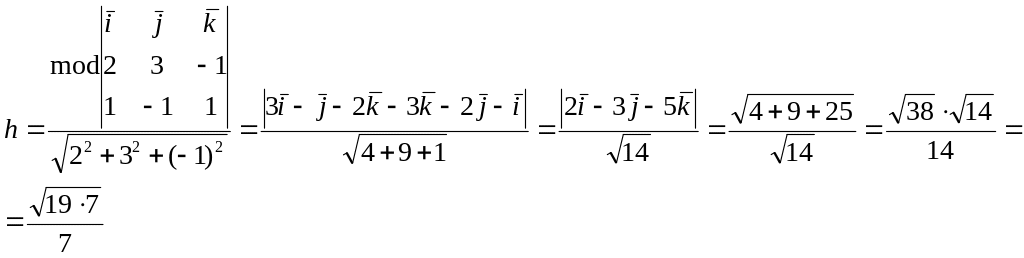
Пример
2.
В
произвольном базисе
вычислить Sпар
основанного
на векторах.
если
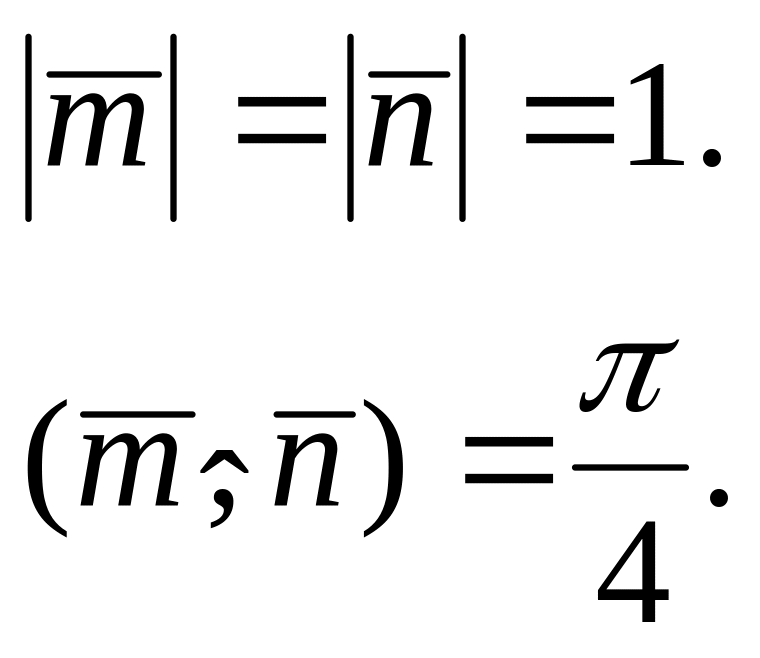
Перемножим векторно и :
