5.1. Геометрический смысл декартовых прямоугольных координат вектора.

Прямоугольные координаты вектора численно равны проекциям этого вектора на базисные орты.

Обозначим углы, образованные ортами и вектором соответственно , , .

Тогда координаты вектора будут: z

^(*)

γ

β y

x α

Косинусы cos, cos, cos  называется направляющими косинусами вектора .

Из равенства ^(*) получаем:

Формулы для нахождения направляющих косинусов.

Свойства направляющих косинусов.

1⁰. cos² + cos² + cos² = 1 – сумма квадратов направляющих косинусов равна1.

2⁰. Пусть .

Найдем орт вектора .

или .

Координаты орты совпадает с направляющими косинусами вектора .

5.2. Условие коллинеарности векторов в координатной форме.

Пусть даны , .

Пусть векторы и коллинеарные, т.е. параллельные отличающиеся только на постоянный множитель.

С ледовательно, x₁ = x₂  = x₁/x₂

y₁ = y₂  = y₁/y₂

z₁ = z₂  = z₁/z₂

Если вектора коллинеарные, то их одноименные координаты пропорциональны.

условие коллинеарности.

5.3. Формулы расстояний в координатной форме.

Рассмотрим точки М, М₁, М₂ в декартовых координатах. Положение  точки можно определить ее радиус – вектора (проведенным из начала координат в М).

Очевидно, что координаты вектора и точки совпадают.

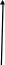
z / M₁(x₁,y₁,z₁)

M (x, y, z).

M₂ (x₂,y₂, z₂).

y

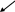⁰

x

Из рисунка видно, что:

Тогда длина вектора по определению:

– формула расстояния между двумя точками.

Рассмотрим отрезок М₁М₂.Точка М взята произвольно. Пусть отношение длин отрезков М₁М и ММ₂ равно ,т.е. .

Запишем вектора в координатной форме

В силу коллинеарности векторов:

║ Û .

А у векторов соответствующие координаты пропорциональны.

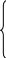x – x₁ =  ( x₂ - x)

y – y₁ =  ( y₂ - y) 

z – z₁ =  ( z₂ – z )

Формулы координат точки делящей отрезок в данном отношении .

- координаты середины отрезка  = 1 (один к одному).