7. Формула полной вероятности. Формула Байеса.
Пусть
– вероятностное пространство некоторого
испытания, а события
попарно несовместны и образуют полную
группу, причём
,
.
Тогда вероятность произвольного события
вычисляется по формуле полной вероятности
.
События
принято называть гипотезами.
Вывод формулы.
События
попарно несовместны и образуют полную
группу, поэтому событие А
является суммой попарно несовместных
событий
.
…
В силу аксиомы сложения
,
а из формулы
умножения вероятностей для двух событий
имеем
,
,
откуда
.
Условная вероятность
гипотезы
(
)
относительно события А
вычисляется по формуле Байеса
,
где .
Вывод формулы.
Из формулы умножения вероятностей имеем
,
откуда
,
где вычисляется по формуле полной вероятности.
Вероятность
называется априорной (доопытной)
вероятностью гипотезы
,
а
– апостериорной (послеопытной)
вероятностью этой гипотезы. Формула
Байеса позволяет переоценивать
вероятности гипотез после проведения
испытания, в результате которого
произошло событие А.
8. Вычисление вероятностей событий с помощью биномиальной и полиномиальной формул.
Пусть некоторое
случайное событие А
в испытании происходит с вероятностью
р
и не происходит с вероятностью
.
Тогда вероятность того, что при n
независимых повторениях испытания в
одинаковых условиях событие А
произойдёт ровно m
раз (
),
вычисляется по формуле
.
Вывод формулы.
Пусть
– событие, состоящее в появлении, а
– в непоявлении события А
в i-м
испытании. Рассмотрим событие В,
состоящее в том, что при n
повторениях испытания событие А
произошло ровно m
раз. Очевидно,
,
где
,
,
... ,
и
.
События
попарно несовместны и каждое из них
является произведением каких-нибудь m
событий
и
событий
.
События-сомножители являются независимыми,
т.к. испытания проводятся независимо
друг от друга.
Испытания проводятся
в одинаковых условиях, поэтому вероятность
события А
не меняется, т.е.
,
,
,
а значит, из теоремы умножения вероятностей
для независимых событий имеем
,
,
где
и
.
В силу попарной
несовместности событий
и аксиомы сложения
,
т.е.
.
Рассмотренная
схема повторных независимых испытаний
называется схемой Бернулли или
биномиальной схемой, а полученная
формула для вероятности
– формулой Бернулли или биномиальной
формулой. Появление рассматриваемого
события А
при повторных независимых испытаниях
принято называть успехом, а непоявление
– неудачей.
Пусть, далее,
– попарно несовместные события,
образующие полную группу, и известны
вероятности
,
.
Из аксиом 2 и 3 следует, что
.
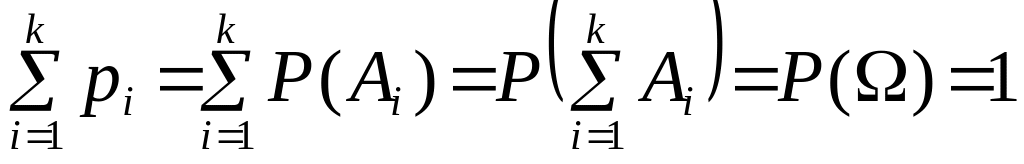Тогда вероятность того, что в серии из
n
независимых испытаний событие
произойдёт
раз,
–
раз, … ,
–
раз, определяется с помощью полиномиальной
формулы
,
где
.
Данная вероятностная схема называется
полиномиальной и представляет собой
обобщение биномиальной схемы.
9. Понятие случайной величины и её закона распределения. Дискретные и непрерывные величины.
Исходами многих экспериментов являются события, связанные с появлением некоторых чисел, при этом в результате опыта каждый раз появляется одно и только одно числовое значение, заранее неизвестное. Примерами таких событий служат выпадение определённого числа гербов при пяти бросаниях монеты, определённое число выстрелов до первого попадания в цель, определённое время безотказной работы радиолампы, определённая масса взятого наугад зерна пшеницы. Подобные примеры приводят к математическому понятию случайной величины.
Пусть
– вероятностное пространство некоторого
испытания. Случайной величиной (СВ)
называется функция
,
которая каждому элементарному событию
ставит в соответствие определённое
числовое значение
,
причём для любого
события
и
принадлежат полю F.
Значение
,
соответствующее конкретному элементарному
событию
,
называется реализацией СВ. Совокупность
всех реализаций называется множеством
возможных значений СВ. Случайные величины
обозначаются буквами
и т.д.
Под законом
распределения СВ Х
понимается любое правило (таблица,
функция, график), позволяющее найти
вероятность события
для произвольного
.
Из определения CВ
Х
и свойств поля F
следует, что при любых
(
)
определены вероятности событий
,
,
,
,
,
,
и т.д.
Случайная величина Х называется дискретной, если множество её возможных значений конечно или счётно, причём вероятность появления каждого отдельного значения отлична от нуля.
Случайная величина Х называется непрерывной, если множество её возможных значений – конечный или бесконечный промежуток числовой прямой, причём вероятность появления каждого отдельного значения равна нулю.
На практике встречаются также случайные величины, множество возможных значений которых – конечный или бесконечный промежуток числовой прямой, но вероятности появления некоторых значений отличны от нуля. Такие СВ называют величинами смешанного типа.