31. Гистограмма и полигон частот.
Пусть Х
– непрерывная СВ, результаты измерений
которой представлены в виде статистического
ряда, т.е. построены интервалы
,
и найдены частоты
,
.
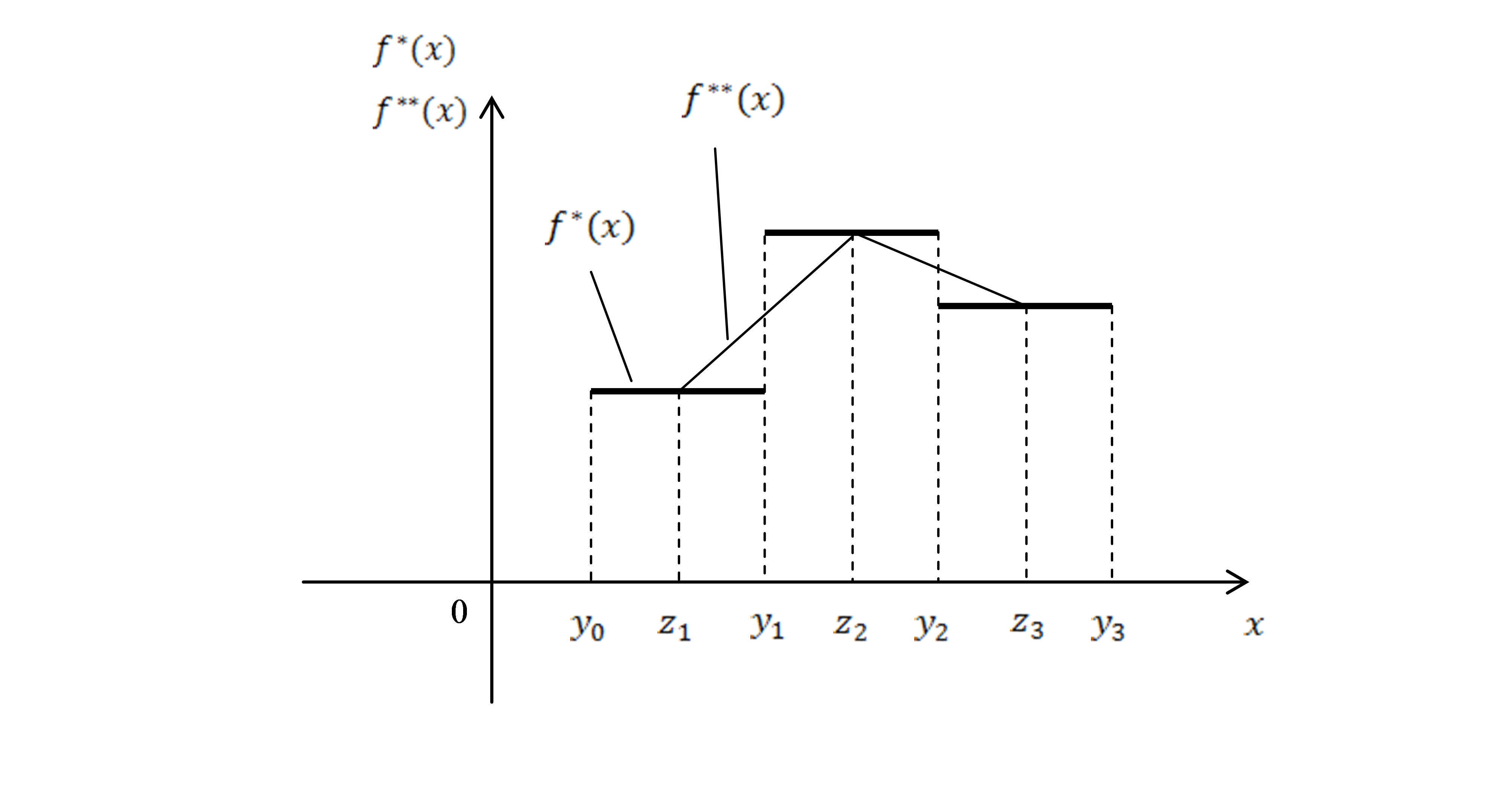
Гистограммой частот называется
кусочно-постоянная функция
,
которая на каждом из интервалов
принимает значение
,
где
есть длина соответствующего интервала.
При
и
полагается
.
Площадь ступенчатой фигуры под графиком
равна сумме частот всех интервалов,
т.е. единице.
Полигоном частот
называется функция
,
графиком которой является ломаная,
последовательно соединяющая точки
,
,
... ,
.
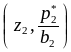Таким образом,
график полигона
– это ломаная, вершины которой расположены
на серединах ступеней графика гистограммы
.
При
и
полагается
.
При большом объёме выборки гистограмма
и полигон частот используются в качестве
оценки плотности распределения
СВ Х.
Пусть теперь Х
– дискретная СВ, результаты измерений
которой представлены в виде статистического
ряда, т.е. определены различные элементы
выборки
,
расположенные в порядке возрастания,
и соответствующие им частоты
.
Тогда полигоном частот называется
функция
,
графиком которой является ломаная,
последовательно соединяющая точки
.
При большом объёме выборки полигон
частот служит статистическим аналогом
многоугольника распределения.
32. Статистическая функция распределения.
Пусть имеется
выборка
измерений некоторой СВ Х
с неизвестной функцией распределения
.
Статистической (эмпирической) функцией
распределения называется функция
,
где n
– объём выборки,
– количество элементов выборки, значения
которых меньше х.
Таким образом, значение статистической
функции распределения
при каждом значении аргумента х
есть частота появления события
в данной серии измерений (наблюдений)
СВ Х.
Статистическая
функция распределения
– неубывающая кусочно-постоянная
функция, скачки которой соответствуют
значениям СВ Х,
имеющимся в выборке, и по величине равны
частотам этих значений. В частности,
если ни одно из этих значений в выборке
не повторяется, то величина каждого
скачка равна
.
Если
–
минимальный, а
–
максимальный элемент выборки, то
при
и
при
.
Поскольку в разных
сериях измерений значения
при различных х
меняются случайным образом, то функция
,
построенная по данным выборки
,
представляет собой реализацию случайной
функции
,
где
– количество элементов случайной
выборки
,
значения которых меньше х.
Из теоремы Бернулли следует, что
сходится по вероятности к
,
т.е. при любых
и
имеет место
.
Пусть, далее, Х
– непрерывная СВ. При большом объёме
выборки построение
становится трудоёмким. Поэтому для
получения статистического аналога
функции распределения
обычно используются данные статистического
ряда. Если построены интервалы
,
и найдены их частоты
,
,
то на правом конце
каждого интервала статистическая
функция
полагается равной
,
т.е. накопленной частоте этого интервала.
При
полагается
,
при
полагается
.
График функции
строится в виде ломаной, последовательно
соединяющей точки
,
,
,
,
... ,
,
где
,
и называется кумулятивной ломаной. При
большом объёме выборки
и
используются в качестве оценки функции
распределения
СВ Х.
