25. Основные свойства дисперсии и коэффициента корреляции.

1⁰. Если с – константа, то .

Доказательство. По определению дисперсии имеем

.

2⁰. Если с – константа, а Х – случайная величина, то .

Доказательство. По определению дисперсии имеем

.

3⁰. Для любых двух СВ Х и Y имеет место

, .

Доказательство. Покажем справедливость первого из равенств (второе доказывается аналогично).

Пусть , тогда . Вычитая почленно из первого равенства второе, получим , а по определению дисперсии

.

Из данного свойства следует, что если СВ Х и Y некоррелированы, то

.

Формула для дисперсии суммы имеет обобщение на случай произвольного числа величин: если – независимые СВ, то

.

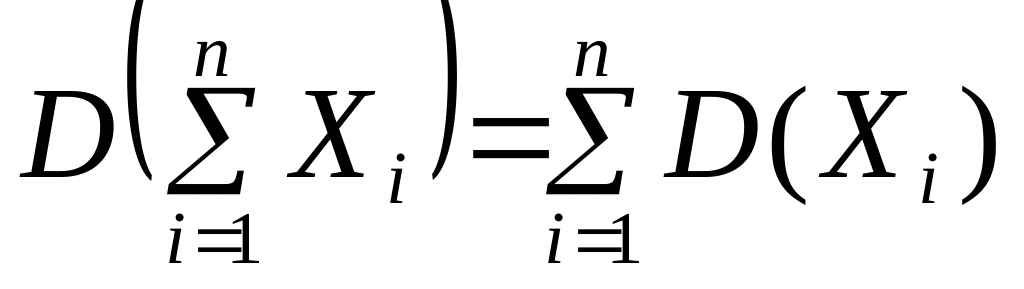4⁰. Для любых двух СВ Х и Y имеет место .

Доказательство. Рассмотрим вспомогательную СВ и найдём её дисперсию:

.

Дисперсия любой СВ неотрицательна, поэтому . Рассмотрев СВ , аналогично найдём . Из двух полученных неравенств имеем . Разделив обе части последнего неравенства на положительную величину , получим .

5⁰. Если СВ Х и Y связаны линейной функциональной зависимостью, т.е. , где и , то при и при .

Доказательство. Пусть , тогда

.

Поскольку , то . Отсюда , т.е. при и при .

26. Распределения “хи-квадрат”, Стьюдента и Фишера.

Пусть – независимые СВ, распределённые по стандартному нормальному закону. Тогда распределение непрерывной СВ называется распределением “хи-квадрат” (или распределением Пирсона) с n степенями свободы. График плотности этого распределения имеет вид:

При имеет место . Для нахождения  из условия при различных n и р составлены таблицы.

Непрерывная СВ , где и СВ Х и независимы, называется дробью Стьюдента с n степенями свободы. График плотности этого распределения имеет вид:

При любом х имеет место . Для нахождения  из условия при различных n и р составлены таблицы. При увеличении n распределение СВ неограниченно приближается к стандартному нормальному распределению.

Непрерывная 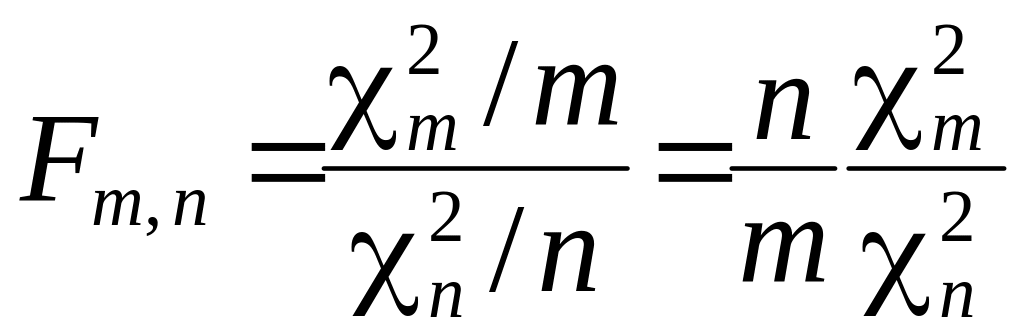СВ , где СВ и независимы, называется дробью Фишера с степенями свободы. График плотности этого распределения имеет вид:

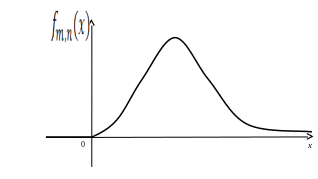
При имеет место . Для нахождения  из условия при различных и близких к нулю р составлены таблицы. Из цепочки равенств

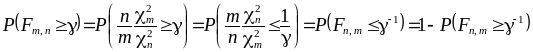
следует, что при близких к единице р соответствующее  можно найти из условия .

27. Закон больших чисел.

Под законом больших чисел понимается совокупность теорем, устанавливающих условия приближения среднего арифметического большого числа случайных величин к некоторым неслучайным величинам.

Приведём сначала одно важное утверждение, используемое при доказательстве закона больших чисел.

Неравенство Чебышёва. Если СВ Х имеет математическое ожидание m и дисперсию D, то для любого справедливо неравенство

.

Доказательство проведём для случая дискретной СВ Х. Поскольку события , попарно несовместны, то . Для дисперсии СВ Х имеем

,

откуда вытекает требуемое неравенство.

Рассмотрим, далее, две формулировки закона больших чисел.

Теорема Чебышёва. Если – независимые СВ, имеющие один и тот же закон распределения с математическим ожиданием m и дисперсией D, то при неограниченном увеличении n случайная величина сходится по вероятности к константе m, т.е. для любого имеет место .

Доказательство. В силу независимости СВ и свойств математического ожидания и дисперсии

и ,

поэтому неравенство Чебышёва для СВ при произвольном имеет вид . Правая часть при увеличении n стремится к нулю, откуда следует справедливость утверждения теоремы.

Замечание. Данная теорема подтверждает тот факт, что при большом числе независимых измерений СВ Х среднее арифметическое результатов измерений почти всегда лишь мало отличается от её математического ожидания. Действительно, если – случайные величины, соответствующие результатам n независимых измерений СВ Х, то они независимы и имеют тот же закон распределения и те же числовые характеристики, что и СВ Х, а значит, к ним применима теорема Чебышёва.

Теорема Бернулли. Если в каждом из n независимых испытаний событие А появляется с одинаковой вероятностью р, то при неограниченном увеличении n частота сходится по вероятности к константе p, т.е. для любого имеет место .

Доказательство. Обозначим через число появлений события А в i-м испытании. Очевидно, – дискретные СВ с возможными значениями 0 и 1, при этом , , . В силу независимости испытаний, СВ независимы, при этом , , и Применяя теорему Чебышёва к СВ , получим утверждение теоремы Бернулли.

Замечание. Данная теорема подтверждает тот факт, что при большом числе независимых испытаний частота события почти всегда лишь мало отличается от его вероятности.