7. Изоморфизм графов. Необходимые условия изоморфизма.
В теории графов изоморфизмом графов и называется биекция между множествами вершин графов такая, что любые две вершины u и v графа G смежны, если и только если вершины f(u) и f(v) смежны в графе H. Здесь графы понимаются неориентированными и не имеющими весов вершин и ребер. В случае, если понятие изоморфизма применяется к ориентированным или взвешенным графам, накладываются дополнительные ограничения на сохранение ориентации дуг и значений весов. Если изоморфизм графов установлен, они называются изоморфными и обозначаются как .
Иногда биекция f записывается в виде подстановки изоморфизма .
Некоторые задачи обработки графов требуют не только проверки изоморфизма, но и выяснения его подстановки.
Отношение изоморфизма графов представляет собой отношение эквивалентности, определенное для графов, и позволяет произвести разбиение исходного класса всех графов на классы эквивалентности. Множество графов, изоморфных друг другу, называется классом изоморфизма графов (англ.), их число в зависимости от n представляет собой последовательность (1, 1, 2, 4, 11, 34, 156, 1044, 12346, ...).
В случае, если биекция f отображает граф сам на себя (графы G и H совпадают), она называется автоморфизмом графа G.
Графы G и H являются изоморфными, если путем перестановки строк и столбцов матрицы смежности графа G удается получить матрицу смежности графа H. Однако перебор всех возможных перестановок характеризуется вычислительной сложностью O(N!) (при условии, что сравнение матриц смежности производится за время, не зависящее от N, что обычно несправедливо и дополнительно увеличивает приведенную оценку), что существенно ограничивает применение подобного подхода на практике. Существуют методы ограниченного перебора возможных пар предположительно-изоморфных вершин (аналог метода ветвей и границ), однако они незначительно улучшают приведенную выше асимптотику[
Биекция (одно-однозначное отношение) — двухместное отношение R, определенное на некотором множестве, отличающееся тем, что в нём каждому значению х соответствует единственное значение у, и каждому значению усоответствует единственное значение х. Одно-однозначное отношение является частным случаем однозначного отношения.
Графы G и H являются изоморфными, если путем перестановки строк и столбцов матрицы смежности графа G удается получить матрицу смежности графа H. Однако перебор всех возможных перестановок характеризуется вычислительной сложностью O(N!) (при условии, что сравнение матриц смежности производится за время, не зависящее от N, что обычно несправедливо и дополнительно увеличивает приведенную оценку), что существенно ограничивает применение подобного подхода на практике. Существуют методы ограниченного перебора возможных пар предположительно-изоморфных вершин (аналог метода ветвей и границ), однако они незначительно улучшают приведенную выше асимптотику.
8. Операции над графами
С помощью различных операций можно строить графы из более простых, переходить от одного графа к более простому, разбивать графы на более простые и т.д. Операции могут быть одноместными и двуместными. Рассмотрим эти операции в порядке возрастания их сложности (начнем с одноместных).
Д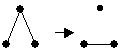
ополнением
графа G1(V1,E1)
называется граф G2(V2,E2),
у которого множество вершин такое же,
как у исходного графа, а множество ребер
представляет собой дополнение до
множества
Вершины
графа G2
смежны только в том случае, когда они
не смежны в исходном графе. Обозначение:
` G1(V1,E1).
Дополнение
графов есть дополнение отношений.
Пример 3.15 Дополнение к полному графу – пустой граф. Другой пример показан на рисунке.
Удаление вершины v из графа G1(V1,E1) (при условии vÎ V1): вершина v удаляется из множества V1, а из множества ребер удаляются ребра, инцидентные этой вершине: V = V1\{v}, E= E1\{e = (v1,v2) | v1 = v или v2 = v}. Обозначение: G = G1(V1,E1)–v.
П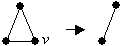
ример
3.16 C3
– v
= K2.
Добавление вершины v в граф G1(V1,E1) (при условии vÏ V1): во множество вершин добавляется вершина v: V = V1È {v}, E = E1. Обозначение: G = G1(V1,E1) + v.
Удаление ребра e из графа G1(V1,E1) (при условии eÎ E1): из множества ребер удаляется ребро e: V = V1, E= E1 \ {e}; его вершины сохраняются. Обозначение: G = G1(V1,E1)–e.
П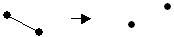
ример
3.17
Добавление ребра e в граф G1(V1,E1) (при условии eÏ E1): во множество ребер добавляется ребро e: V = V1, E = E1È {e}. Обозначение: G = G1(V1,E1)+e.
Отождествление вершин v1,v2 графа G1(V1,E1): замена этой пары новой вершиной v, причем все ребра, которые вели в удаленные вершины, заменяются ребрами, ведущими в v. Если эти вершины были смежными, то их отождествление называется стягиванием ребра.
Пример 3.18 (4,4)-граф после стягивания ребра превратился в K2.
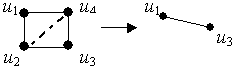
Стягивание подграфа А графа G1(V1,E1) (при условии AÌ V1): из множества вершин удаляется множество A и заменяется новой вершиной v, все ребра, которые вели в вершины из А, заменяются ребрами, ведущими в v. V = V1 \ A È {v}, E= E1 \ {e = (u,v) | uÎ A или vÎ A}È {e = (u,v) | uÎ Г(A)\A}. Обозначение: G = G1(V1,E1)/A.
Пример 3.19 K4 / C3 =K2.
Подразбиение ребра графа G1(V1,E1): удаление ребра и добавление новой вершины, которая соединяется ребром с каждой вершиной удаленного ребра.
Размножение вершины v графа G1(V1,E1) (при условии vÎ V1, v’Ï V1): во множество вершин добавляется вершина v’, во множество ребер – ребра, соединяющие новую вершину v’ с вершиной v и со всеми смежными с ней вершинами. V = V1 È {v’}, E = E1 È {(v,v’)} È {e = (u,v’) | uÎ Г+(v)}. Обозначение: G = G1(V1,E1) v.
Пример
3.20
Объединением графов G1(V1,E1) и G2(V2,E2) (при условии, что их множества вершин, как и множества ребер, не пересекались) называется граф G(V,E), в котором V = V1È V2, E = E1È E2. Обозначение: G = G1È G2.
Пример 3.21 ` K3,3.= C3È C3. Любой граф является объединением своих компонент связности.
Соединением графов G1(V1,E1) и G2(V2,E2) (также при условии, что их множества вершин и множества ребер не пересекались) называется граф G(V,E), в котором V = V1È V2, E= E1È E2È {e=(v1,v2) | v1Î V1, v2Î V2}. Иными словами, строится объединение графов и добавляются ребра, соединяющие графы G1(V1,E1) и G2(V2,E2). Обозначение: G = G1+G2.
Пример 3.22 Km,n.=` Km +` Kn.
Произведением графов G1(V1,E1) и G2(V2,E2) (также при условии, что их множества вершин и множества ребер не пересекались) называется граф G(V,E). В нем V = V1×V2, и вершины (u1,u2) и (v1,v2) смежны только в том случае, если либо u1=v1 и u2 смежна с v2, либо u2=v2 и u1 смежна с v1. Обозначение: G = G1×G2.
Пример 3.23
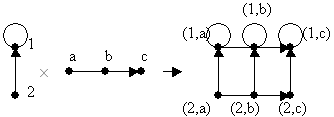
Операции над графами могут использоваться для построения графов с заданными свойствами.