20. Момент инерции материальной точки, системы материальных точек, твердого тела относительно оси.

Момент инерции материальной точки относительно оси - произведение массы материальной точки на квадрат ее расстояния до оси.

Определение: Моментом инерции материальной точки относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой точки при вращательном движении и, равная произведению её массы на квадрат расстояния до оси, т.е. , а также , где - угловая скорость тела относительно данной оси.

Моментом инерции твердого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до оси.

Определение: Моментом инерции системы материальных точек относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой системы при вращательном движении и, равная алгебраической сумме произведений масс всех материальных точек системы на квадрат их расстояний до оси, т.е. . момент инерции определен только относительно оси.

21. Свойства момента инерции тела относительно оси. Теорема Штейнера.

Итак, перечислим свойства момента инерции относительно данной оси, которую мы назовем осью z:

1. Момент инерции равен

2. Если предмет состоит из нескольких частей, причем момент инерции каждой из них известен, то полный момент инерции равен сумме моментов инерции этих частей.

3. Момент инерции относительно любой данной оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение полной массы на квадрат расстояния данной оси от центра масс

4. Момент инерции плоской фигуры относительно оси, перпендикулярной к ее плоскости, равен сумме моментов инерции относительно любых двух других взаимно перпендикулярных осей, лежащих в плоскости фигуры и пересекающихся с перпендикулярной осью.

 

В табл. 19.1 приведены моменты инерции некоторых элементарных фигур, имеющих однородную плотность масс, а в табл. 19.2 — моменты инерции некоторых фигур, которые могут быть получены из табл. 19.1 с использованием перечисленных выше свойств.

Теорема Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:

где

— известный момент инерции относительно оси, проходящей через центр масс тела,

— искомый момент инерции относительно параллельной оси,

 — масса тела,

 — расстояние между указанными осями.

22. Главные и свободные оси инерции тела. Главные моменты инерции. Устойчивые оси вращения.

Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями (иногда их называют главными осями инерции). Через любую точку, взятую в плоскости сечения, можно провести в общем случае две главных оси (в некоторых частных случаях их может быть бесчисленное множество). Для того чтобы убедиться в справедливости этого утверждения, рассмотрим, как изменяется центробежный момент инерции при повороте осей на 90° (рис.2.9).

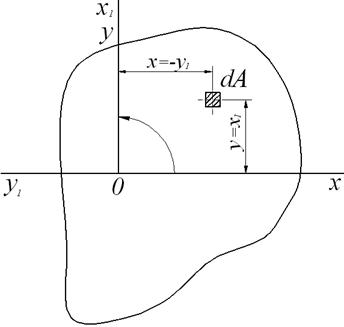
Рис.2.9. К определению положения главных осей

Для произвольной площадки , взятой в первом квадранте системы осей обе координаты, а, следовательно, и их произведение, положительны. В новой системе координат, повернутой относительно первоначальной на 90°, произведение координат рассматриваемой площадки отрицательно. Абсолютная величина этого произведения не изменяется, т. е. Очевидно, то же имеет место и для любой другой элементарной площадки. Значит и знак суммы представляющей собой центробежный момент инерции сечения, при повороте осей на 90° меняется на противоположный, т. е.

величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

mi — масса i-й точки,

ri — расстояние от i-й точки до оси.