8)Свойства гидростатического давления.

1. Гидростатическое давление всегда направлено по нормали к поверхности и его величина не зависит от ориентации поверхности.

2. Внутри покоящейся жидкости в любой точке гидростатическое давление направлено по внутренней нормали к площадке, проходящей через эту точку.

Причем p_x = p_y = p_z = p_n.

3. Для любых двух точек одного и того же объема однородной несжимаемой жидкости (ρ = const)

ρ₁ + ρП₁ = ρ₂ + ρП₁

где ρ – плотность жидкости;

П₁, П₂ – значение поле массовых сил в этих точках.

Поверхность, для любых двух точек которой давление одно и то же, называется поверхностью равного давления.

4.Если в Ж провести гор.площадку, давление в каждой точки будет одинаково.

9)Уравнение Эйлера для покоящейся жидкости.

Выделим в жидкости объём в форме параллелепипеда. Используем принцип затвердевания и поместим его в систему координат.

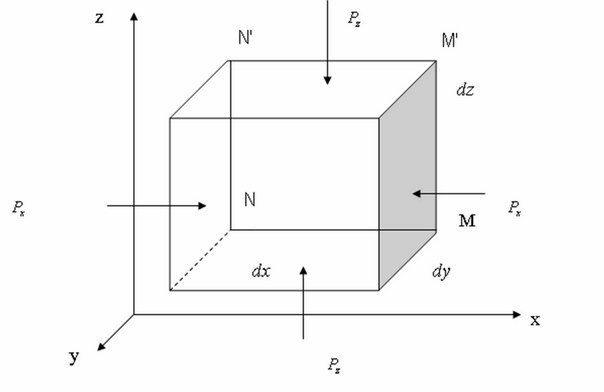
Рисунок 2.3 - Схема для вывода дифференциальных уравнений равновесия идеальной жидкости

 – давление в точке N (при переходе от M к N)

 – для N' и M'

Разделим эти уравнения на массу ρdxdydz параллелепипеда и получим

Уравнение (2.2) называется дифференциальным уравнением Эйлера. Умножим соответственно на dx, dy, dz и просуммируем

Если действует только сила тяжести, то X = Y =0  Z = –g

И уравнение Эйлера примет вид

Заменяя в уравнении (2.5) на h – глубину расположения точки, найдем

Гидростатический напор для покоящейся жидкости постоянен.

10)Основное уравнение гидростатики

энергетический и геометрический смысл

,

где

 — гидростатическое давление (абсолютное или избыточное) в произвольной точке жидкости,

 — плотность жидкости,

 — ускорение свободного падения,

 — высота точки над плоскостью сравнения (геометрический напор^[2]),

 — гидростатический напор^[3].

Энергетический смысл: р/ - удельная (отнесенная к единице веса) потенциальная энергия давления, z - удельная потенциальная энергия положения.

Геометрический смысл: p/ + z = Н - гидростатический напор, тогда: p/ - пьезометрический напор и z - напор положения.

11)Закон Паскаля.

Величина Р₀  является одинаковой для всех точек объёма жидкости, поэтому, учитывая свойства гидростатического давления можно сказать, что давление, приложенное к внешней поверхности жидкости передается всем точками этой жидкости по всем направлениям одинаково – закон Паскаля.

Плоскость, во всех точках которой давление одинаково – плоскость уровня.

,

где z – геометрическая высота,

– пьезометрическая высота,

 – гидростатический напор.