
- •Глава 1. Основные понятия
- •§1 Операции над комплексными числами
- •§2 Комплексная плоскость
- •§3 Некоторые понятия, относящиеся ко множествам. Кривые на комплексной плоскости.
- •§4 Функции комплексного переменного
- •§5 Функциональные последовательности и ряды
- •§6 Степенные ряды
- •Глава 2. Аналитические функции. Конформные отображения.
- •§1 Аналитические функции
- •§2 Конформные отображения
- •Глава 3. Примеры конформных отображений
- •§1 Дробно линейное отображение
- •§3 Функция
- •§4 Функция Жуковского
- •§7 Таблица некоторых конформных отображений.
- •Глава 4. Теория интеграла
- •§1. Понятие интеграла. Теорема Коши.
- •§2 Интеграл Коши
- •§3 Первообразная.
- •Глава 5. Ряды Тейлора и Лорана
- •§1 Ряд Тейлора аналитической функции
- •§2 Единственность аналитической функции. Принцип максимума модуля.
- •§3 Ряды Лорана
- •§4 Изолированные особые точки однозначных аналитических функций.
- •Глава 6. Элементы теории вычетов и их использование при вычислении интегралов
- •§1 Вычеты
- •§2. Вычисление интегралов
- •§3 Простейшие классы аналитических функций.
- •Глава 7. Преобразование Лапласа.
- •§1 Преобразование Лапласа.
- •§2 Свойства преобразования Лапласа
- •Глава 8. Приложения.
- •§1 Комплексный потенциал
- •§2 Операционное исчисление
§5 Функциональные последовательности и ряды
Если
fn(z)
- однозначные
функции,
то
комплексный ряд
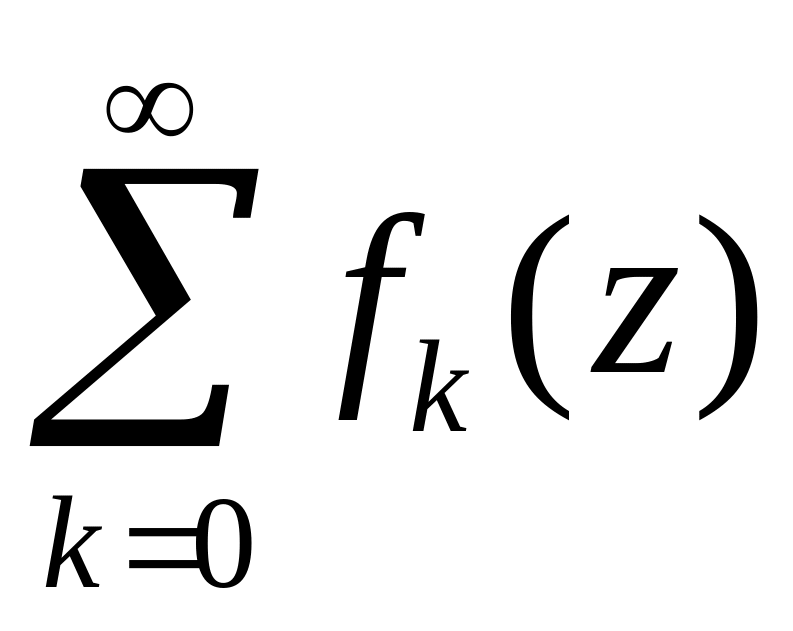 определяется,
как сумма
определяется,
как сумма
![]() =
= .
.
Ряд
называется равномерно
сходящимся на
D,
если его частичные суммы
 равномерно
сходятся на D
к некоторой функции S(z),
т. е.
равномерно
сходятся на D
к некоторой функции S(z),
т. е.
![]() .
.
Критерий Кош равномерной сходимости: Для равномерной сходимости ряда необходимо и достаточно выполнения условия Коши
 .
.
Следствие
(Необходимое условие сходимости). Если
ряд
сходится
в точке
z
,
то
общий член этого ряда
![]() стремится
к нулю в этой точке.
стремится
к нулю в этой точке.
Аналогичное утверждение можно сформулировать для равномерной сходимости:
Если ряд равномерно сходится на D , то общий член этого ряда равномерно стремится к нулю на D.
Достаточный признак Вейерштрасса:
Если
![]() и
числовой
вещественный ряд
и
числовой
вещественный ряд
![]() сходится,
то ряд
сходится
на
D
равномерно.
сходится,
то ряд
сходится
на
D
равномерно.
Полезная теорема. Сумма равномерно сходящегося ряда из непрерывных функций (равномерная сходимость на компакте), есть функция непрерывная.
§6 Степенные ряды
1. Основные свойства степенных рядов.
Напоминание:
Признаки Даламбера и Коши для положительных
рядов (вещественных)  .
.
Даламбер:
Если
для положительного ряда
 существует
предел
существует
предел
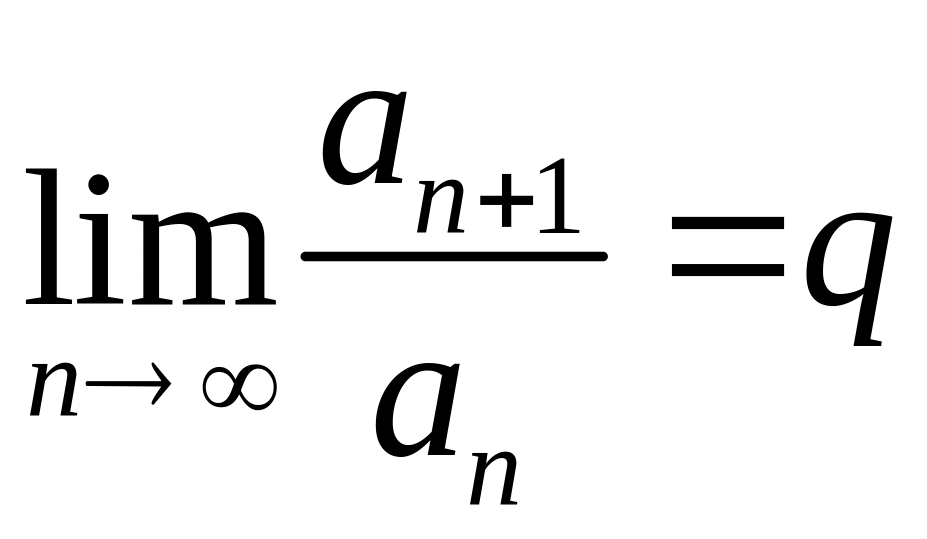 ,
то
при
q
< 1,
ряд сходится, при
q
> 1, расходится.
,
то
при
q
< 1,
ряд сходится, при
q
> 1, расходится.
Определение
верхнего предела
![]() .
.
Коши:
Если
для положительного ряда
существует
предел
![]() ,
то
при
q
< 1, ряд
сходится, при
q
> 1, расходится.
,
то
при
q
< 1, ряд
сходится, при
q
> 1, расходится.
Комплексные
степенные ряды:
 или
или
 (1)
(1)
Теорема 1 (Первая теорема Абеля ) Если ряд (1) сходится в точке z0 0, то он сходится абсолютно в круге |z| < |z0|.
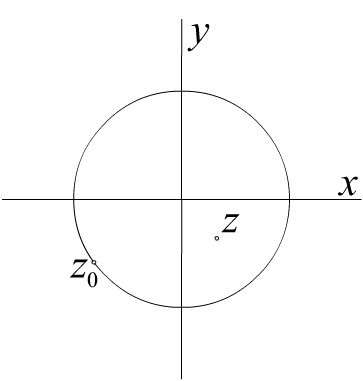
Рис. 1.13.
Доказательство:
Ряд
 сходится, следовательно, согласно
необходимому условию сходимости ряда,
будет выполнено
сходится, следовательно, согласно
необходимому условию сходимости ряда,
будет выполнено
![]() ,
откуда следует, что
,
откуда следует, что
![]() .
Поэтому для общего члена ряда (1) можно
выписать оценку:
.
Поэтому для общего члена ряда (1) можно
выписать оценку:
 ,
при
,
при
![]() .
Таким образом, ряд из модулей исходного
ряда мажорируется (оценивается сверху)
сходящимся рядом
.
Таким образом, ряд из модулей исходного
ряда мажорируется (оценивается сверху)
сходящимся рядом
 в
каждой точке круга
в
каждой точке круга
![]() .
.
Следствие
1.
Для
любого степенного ряда
(1) существует
число
![]() такое,
что при
|z|<R
ряд
сходится, при
|z|>R
ряд
расходится. Это число называется радиусом
сходимости
степенного
ряда. Круг
{|z|
< R}
называется
кругом
сходимости.
такое,
что при
|z|<R
ряд
сходится, при
|z|>R
ряд
расходится. Это число называется радиусом
сходимости
степенного
ряда. Круг
{|z|
< R}
называется
кругом
сходимости.
Следствие
2.
Радиус
сходимости комплексного степенного
ряда
совпадает
с радиусом сходимости вещественного
степенного ряда
 .
.
Для
этого утверждения необходимо сначала
показать, что ряды
и
 имеют один и тот же радиус сходимости.
имеют один и тот же радиус сходимости.
Действительно, пусть их круги сходимости имеют радиусы R1, R2. Во всех точках |z|<R1 ряд сходится абсолютно и, следовательно, ряд тоже сходится абсолютно, т.к. модули общих членов этих рядов одинаковы. По этой же причине справедливо обратное утверждение, во всех точках |z|<R2 будет сходится абсолютно не только ряд , но и ряд . После этого можно рассмотреть ряды и и показать, что они имеют один и тот же радиус сходимости, используя первую теорему Абеля.
В частности, справедливо
Следствие 3. Комплексный ряд с вещественными коэффициентами имеет тот же радиус сходимости, что и вещественный ряд с этими коэффициентами.
Теорема 2 (Вторая теорема Абеля ) Если ряд имеет радиус сходимости R, то он сходится равномерно в любом замкнутом круге радиуса r < R.

Рис. 1.14.
Доказательство:
По первой теореме Абеля ряд
 сходится, кроме того
сходится, кроме того
 для всех z:
|z|
для всех z:
|z|
![]() r.
По признаку Вейерштрасса ряд сходится
равномерно на этом множестве.
r.
По признаку Вейерштрасса ряд сходится
равномерно на этом множестве.
Теорема
(Коши, Адамар)
Радиус сходимости ряда
определяется по формуле
 .
.
Согласно
следствию 2 из первой теоремы Абеля,
радиус сходимости комплексного степенного
ряда совпадает с радиусом сходимости
вещественного степенного ряда
,
радиус сходимости которого определяется
по формуле
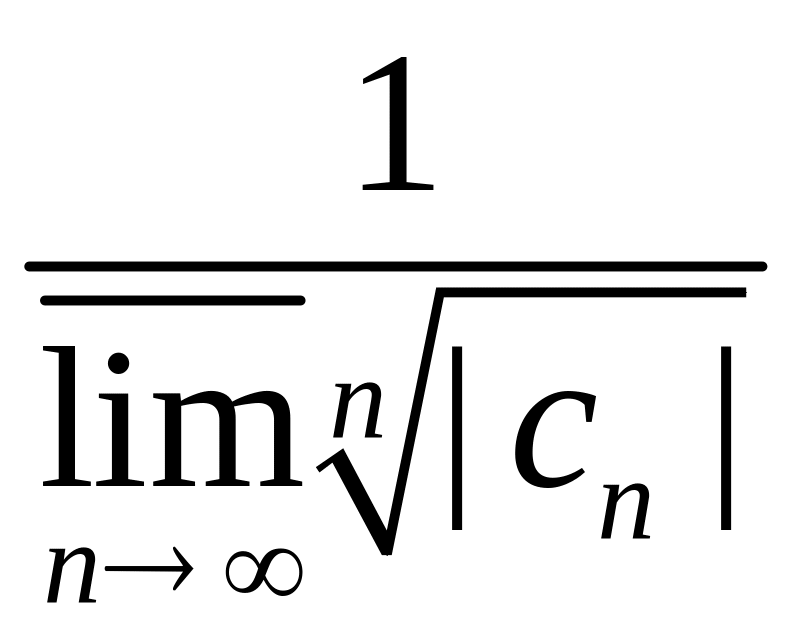 .
.
Примеры:
1)
 ,
имеем cn
= 0,
если n
k2,
cn
= 2k,
если n
= k2.
Поэтому
,
имеем cn
= 0,
если n
k2,
cn
= 2k,
если n
= k2.
Поэтому
![]() ,
так остальные коэффициенты при n
0,cn=0.
Далее
,
так остальные коэффициенты при n
0,cn=0.
Далее
![]() .
.
2) Функция
![]() .
По
определению полагаем
.
По
определению полагаем
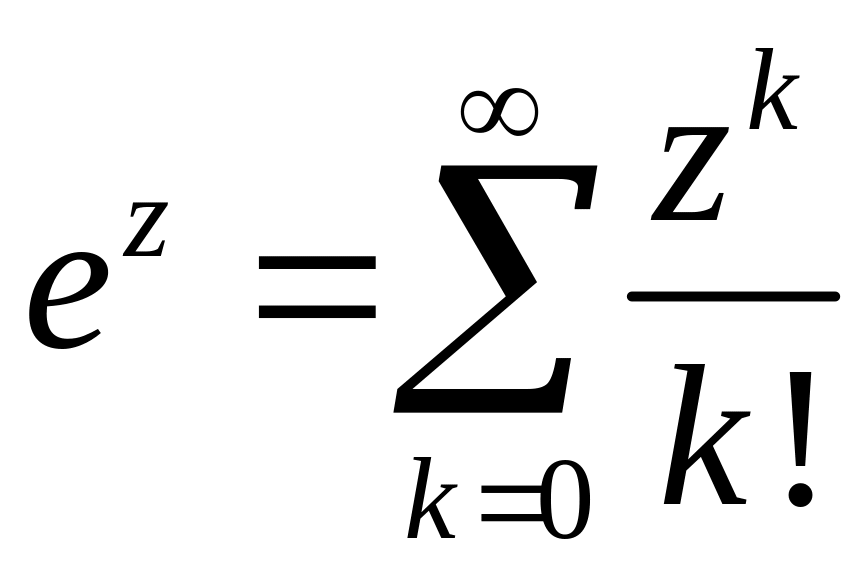 ,
по признаку Даламбера радиус сходимости
такого ряда будет равен R
= .
То же самое можно установить, используя
следствие 2 из первой теоремы Абеля .
,
по признаку Даламбера радиус сходимости
такого ряда будет равен R
= .
То же самое можно установить, используя
следствие 2 из первой теоремы Абеля .
3) Функция
![]() .
По определению полагаем
.
По определению полагаем
 ,
рассматривая соответствующий вещественный
ряд и используя следствие 2 из первой
теоремы Абеля, получим R
= .
Из определения следует, что sin
(-z)
= - sin
z.
,
рассматривая соответствующий вещественный
ряд и используя следствие 2 из первой
теоремы Абеля, получим R
= .
Из определения следует, что sin
(-z)
= - sin
z.
4) Функция
![]() .
По определению полагаем
.
По определению полагаем
 ,
рассматривая соответствующий вещественный
ряд и, используя следствие 2 из первой
теоремы Абеля, получим R
= .
Из определения следует, что cos
(-z)
= cos
z.
,
рассматривая соответствующий вещественный
ряд и, используя следствие 2 из первой
теоремы Абеля, получим R
= .
Из определения следует, что cos
(-z)
= cos
z.
5) Функция
![]() .
По определению полагаем
.
По определению полагаем
 ,
рассматривая соответствующий вещественный
ряд и, используя следствие 2 из первой
теоремы Абеля, получим R
= .
,
рассматривая соответствующий вещественный
ряд и, используя следствие 2 из первой
теоремы Абеля, получим R
= .
6) Функция
![]() .
По определению полагаем
.
По определению полагаем
 ,
рассматривая соответствующий вещественный
ряд и, используя следствие 2 из первой
теоремы Абеля, получим R
= .
,
рассматривая соответствующий вещественный
ряд и, используя следствие 2 из первой
теоремы Абеля, получим R
= .
2. Свойства экспоненциальной и основных тригонометрических функций.
a)
![]() ,
действительно
,
действительно
 .
.
Следствие:
c)
 .
.
Пример:
 при y
.
Синус (и косинус) по модулю может быть
больше единицы в комплексной области.
при y
.
Синус (и косинус) по модулю может быть
больше единицы в комплексной области.
d) eu+v=eu ev

e)
![]() ,
таким образом 2
i
является
периодом, откуда следует, что sin
и cos
имеют период 2
и
в комплексной области.
,
таким образом 2
i
является
периодом, откуда следует, что sin
и cos
имеют период 2
и
в комплексной области.
f) Из c) и d) следует, что sin2 z + cos2 z = 1 (непосредственная проверка).
g) sin iz = i sh z, cos iz = ch z, ch2z – sh2z = 1. Доказывается, используя формулы Эйлера.
