
- •Часть V. Элементы линейного программирования.
- •Глава 2. Транспортная задача.
- •§1. Общая постановка задачи.
- •§2. Методы построения опорного плана перевозок.
- •§3. Метод потенциалов улучшения опорного (первоначального) плана.
- •Алгоритм решения транспортной задачи методом потенциалов.
- •Предварительный шаг решения:
- •Общий шаг решения:
§3. Метод потенциалов улучшения опорного (первоначального) плана.
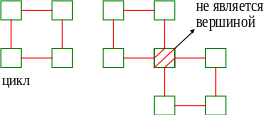
Определение 1. Циклом в таблице называется ломаная, с вершинами в клетках таблицы и звеньями, лежащими вдоль строк и столбцов, если выполняются условия:
Ломаная должна быть связанной, т. е. из любой вершины можно попасть в любую другую.
В каждой вершине ломаной встречаются два звена, одно из которых расположено по строке, другое - по столбцу.
Число вершин ломаной - четное.
 SHAPE \* MERGEFORMAT
SHAPE \* MERGEFORMAT

Первоначальный план, как правило, ацикличен.
Теорема.
Чтобы план
перевозок
 был оптимальным, необходимо и достаточно,
чтобы ему соответствовала такая
система
из
был оптимальным, необходимо и достаточно,
чтобы ему соответствовала такая
система
из
![]() чисел
чисел
![]() ,
для которых выполняются следующие
условия:
,
для которых выполняются следующие
условия:
 (для
всех клеток принадлежащих множеству
X
или для
заполненных
клеток).
(для
всех клеток принадлежащих множеству
X
или для
заполненных
клеток). (для всех клеток,
не принадлежащих множеству Х
или для всех пустых
клеток).
(для всех клеток,
не принадлежащих множеству Х
или для всех пустых
клеток).
Числа
 называют потенциалами
соответствующих пунктов отправления
и назначения.
называют потенциалами
соответствующих пунктов отправления
и назначения.
Алгоритм решения транспортной задачи методом потенциалов.
Определение
2.
Совокупность
уравнений вида
![]() для всех клеток с перевозками
образует систему
для всех клеток с перевозками
образует систему
![]() уравнений с
уравнений с
![]() переменными. Такая система имеет
бесконечное
множество
решений.
Чтобы система была определенной, принято
считать
переменными. Такая система имеет
бесконечное
множество
решений.
Чтобы система была определенной, принято
считать
![]() .
Оставшиеся переменные находят из
системы.
.
Оставшиеся переменные находят из
системы.
Предварительный шаг решения:
составляем опорное решение задачи одним из трех методов.
строим систему потенциалов для клеток с перевозками.
проверяем на потенциальность незаполненные клетки с помощью неравенства . Если все клетки потенциальны, то оптимальный план найден, если нет, то переходим к общему шагу и повторяем его до тех пор, пока не будет найдено оптимальное решение.
каждый раз вычисляем значение функции Z.
для всех не потенциальных клеток вычисляем разности
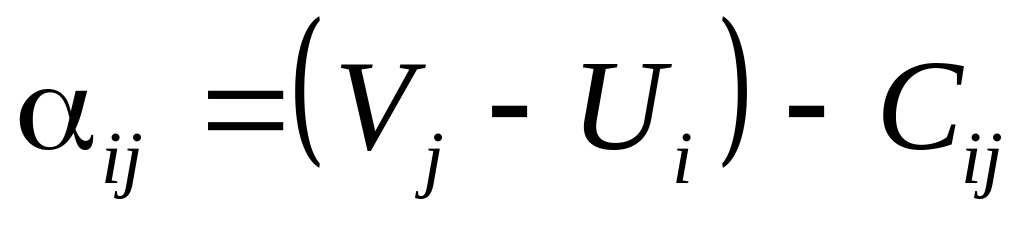 и находим
максимальную
разность.
и находим
максимальную
разность.
Общий шаг решения:
Улучшаем план перевозок, составляя цикл, в одной из вершин которого находится максимально не потенциальная клетка, т. е. соответствующая
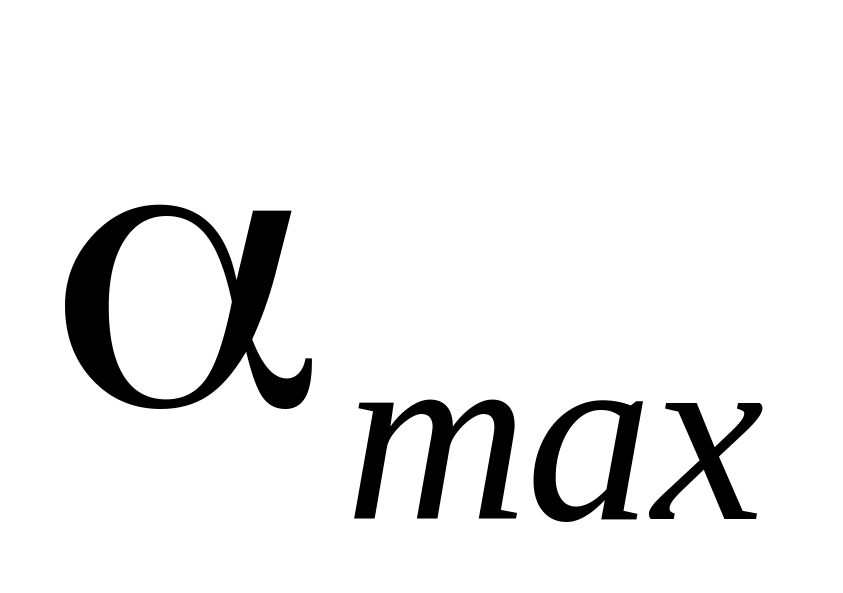 .
Остальные вершины цикла находятся в
заполненных
клетках.
Вершины
цикла,
начиная с максимально не потенциальной
клетки, обозначают знаками
.
Остальные вершины цикла находятся в
заполненных
клетках.
Вершины
цикла,
начиная с максимально не потенциальной
клетки, обозначают знаками
 .
Рассматривают перевозки в отрицательных
вершинах
и находят среди них наименьшую
.
Рассматривают перевозки в отрицательных
вершинах
и находят среди них наименьшую
 .
Далее эту минимальную
перевозку
перемещают по циклу, вычитая от перевозок
с отрицательными
вершинами
и прибавляя к перевозкам с положительными
вершинами.
.
Далее эту минимальную
перевозку
перемещают по циклу, вычитая от перевозок
с отрицательными
вершинами
и прибавляя к перевозкам с положительными
вершинами.Исправляем систему потенциалов: потенциал
 новой клетки оставляют без изменения,
а от соответствующего потенциала
новой клетки оставляют без изменения,
а от соответствующего потенциала
 вычитают
.
Затем
исправляют
систему потенциалов для клеток с
положительными перевозками, для которых
потенциальность нарушена.
вычитают
.
Затем
исправляют
систему потенциалов для клеток с
положительными перевозками, для которых
потенциальность нарушена.Проверяем на потенциальность не заполненные клетки и решаем задачу дальше.
Замечание:
Если задача
решается на max,
то система потенциалов
составляется так же, а условие
потенциальности незаполненных клеток
имеет
вид:
![]() .
.
Пример: Пусть каким- либо образом получен первоначальный план перевозок.
-
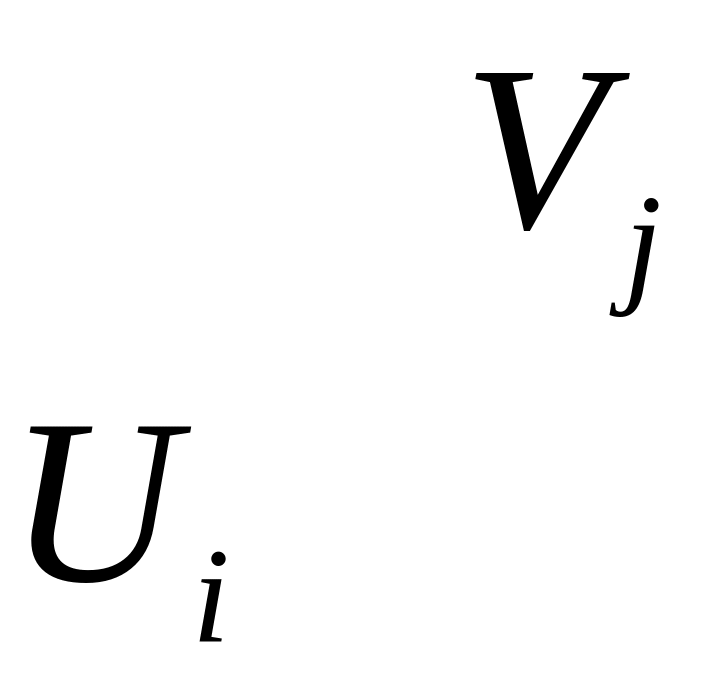
0
5
7
2
Запасы
0
3
5
30
7
10
11
40
-1
1
20
4
6
3
10
30
-5
5
8
12
5
7
15
20
Потребности
20
30
15
25
90
![]()
1) Составим систему потенциалов для заполненных клеток:
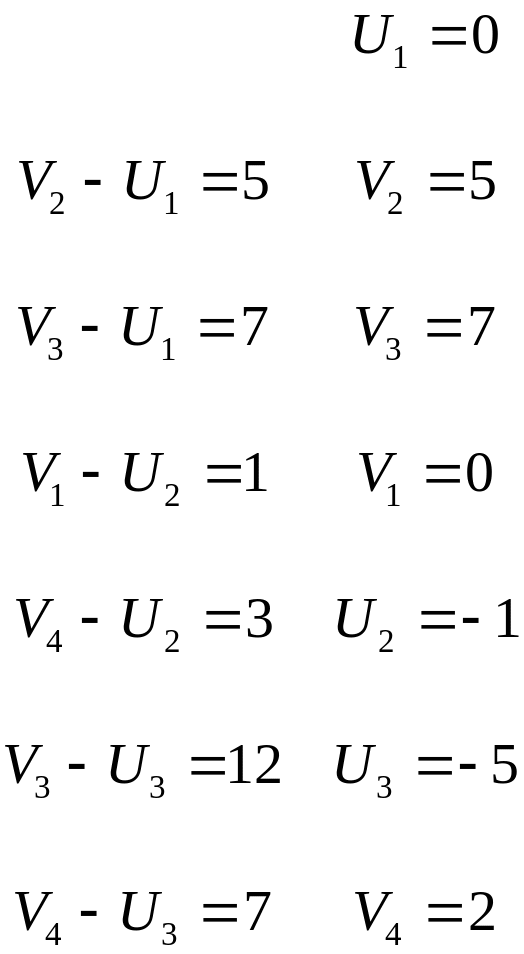
2) Проверим на потенциальность незаполненные клетки.

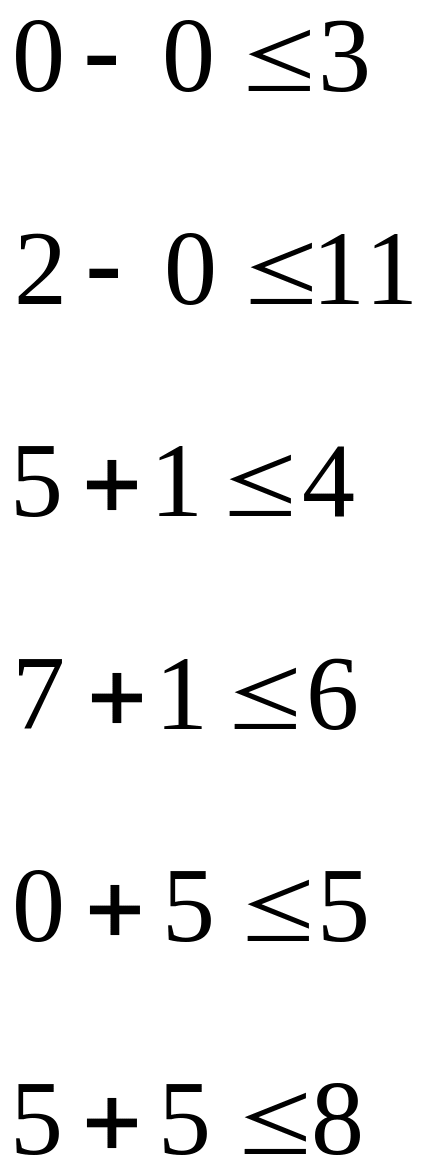
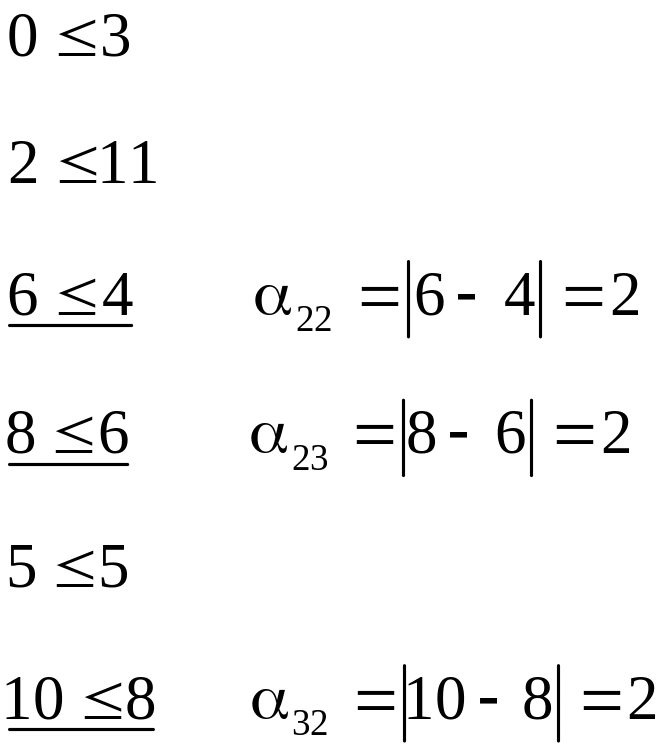
Надо из всех
![]() выбрать максимальную,
но они равны. Следовательно, можно брать
любое значение.
выбрать максимальную,
но они равны. Следовательно, можно брать
любое значение.
3) Составим цикл с
клеткой
![]() :
:

-
3
 5
530

7
10
11
1
2
 0
04
6
3
20
5
8
12
5
7
15
4) Перемещаем отрицательную перевозку «5» по циклу, вычитая ее от клеток с отрицательными перевозками и прибавляя к клеткам с положительными перевозками.
-
2
5
7
4
0
3
5
25
7
15
11
1
1
20
4
6
3
10
-3
5
8
5
12
0
7
15
![]()
5) Меняем систему потенциалов для заполненных клеток:
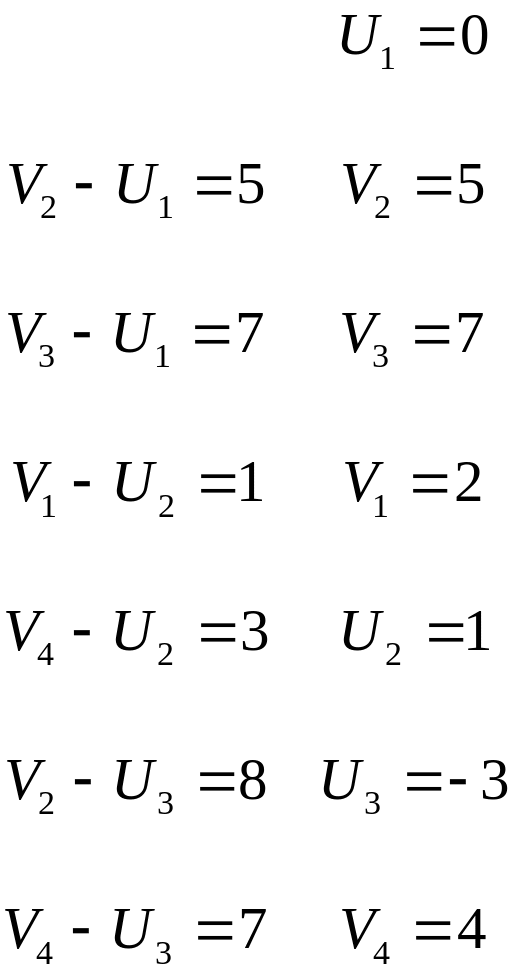
6) Проверяем потенциальность незаполненных клеток:
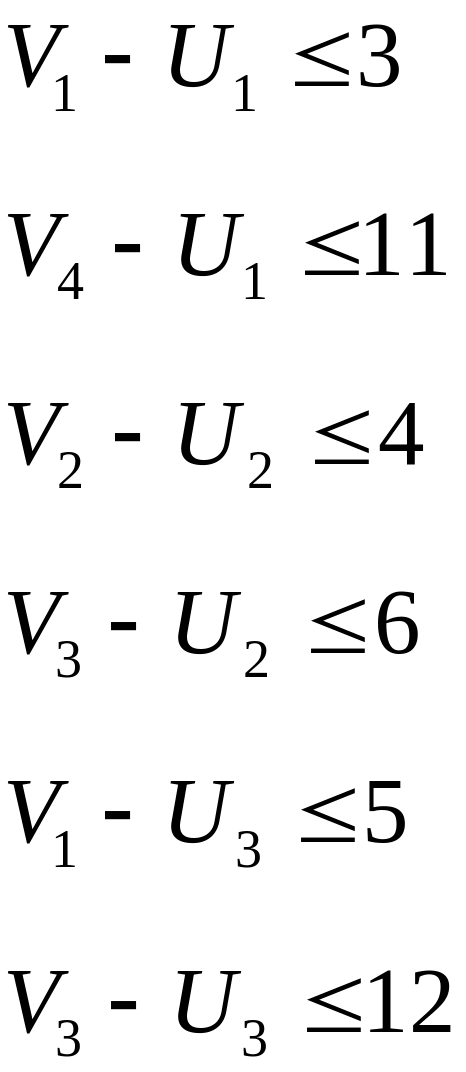
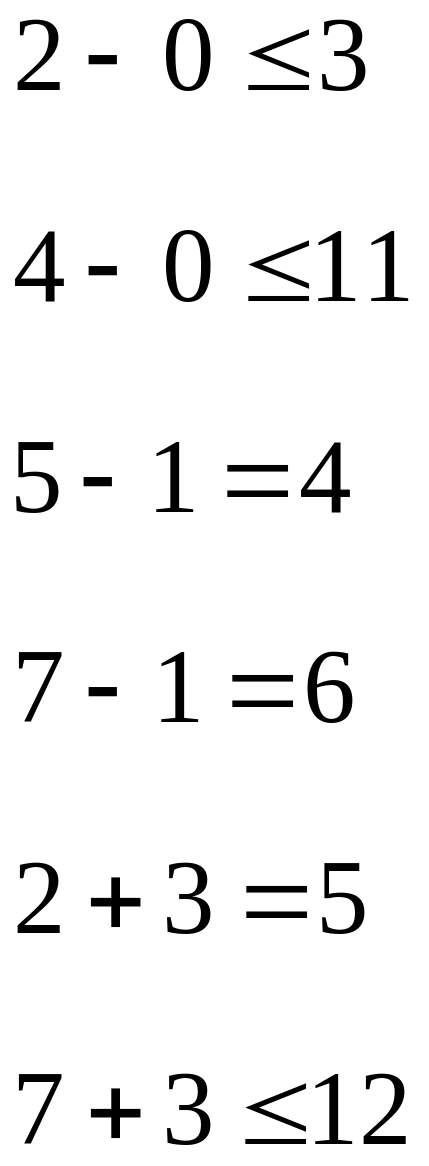
Таким образом, все пустые клетки в полученном плане потенциальны. Следовательно, данное решение оптимальное.
