7/6Термическое уравнение состояния

Термическое уравнение состояния связывает макроскопические параметры системы. Для системы с постоянным числом частиц его общий вид можно записать так: Таким образом, задать термическое уравнение состояния значит конкретизировать вид функции 

Калорическое уравнение состояния

Калорическое уравнение состояния показывает, как внутренняя энергия выражается через давление, объем и температуру. Для системы с постоянным числом частиц оно выглядит так: или, учитывая, что давление можно выразить из термического уравнения:

Каноническое уравнение состояния

Основная статья: Термодинамические потенциалы.

Каноническое уравнение представляет собой выражение для одного из термодинамических потенциалов (внутренней энергии,энтальпии, свободной энергии или потенциала Гиббса) через независимые переменные, относительно которых записывается его полный дифференциал.

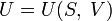•  (для внутренней энергии),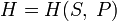

•  (для энтальпии),

•  (для энергии Гельмгольца),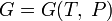

•  (для потенциала Гиббса).

Каноническое уравнение, независимо от того, в каком из этих четырех видов оно представлено, содержит полную информацию о термических и калорических свойствах термодинамической системы (предполагается, что известно и определение термодинамического потенциала, такое, как F = U − TS).

7/7 Равнове́сный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близкихравновесных термодинамических состояний.

Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений.

Реальные процессы изменения состояния системы всегда происходят с конечной скоростью, поэтому не могут быть равновесными. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается, поэтому равновесные процессы называют квазистатическими.

7/8 Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.

Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:

,где  — подведённая к телу теплота, измеренная в джоулях

• ^[1] — работа, совершаемая телом против внешних сил, измеренная в джоулях

Эта формула является математическим выражением первого начала термодинамики

Для квазистатических процессов выполняется следующее соотношение:

, где

•  — температура, измеренная в кельвинах

•  — энтропия, измеренная в джоулях/кельвин

•  — давление, измеренное в паскалях

•  — химический потенциал

•  — количество частиц в системе

7/9 Согласно закону Джоуля, выведенному эмпирически, внутренняя энергия идеального газа не зависит от давления или объёма. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определениюмолярной теплоёмкости при постоянном объёме, 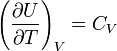 . Так как внутренняя энергия идеального газа является функцией только от температуры, то .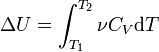

Эта же формула верна и для вычисления изменения внутренней энергии любого тела, но только в процессах при постоянном объёме (изохорных процессах); в общем случае   является функцией и температуры, и объёма.

Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим: ,где   — количество вещества,   — изменение температуры.

7/10  Одним из первых и важных успехов МКТ было качественное и количественное объяснение давления газа на стенки сосуда. Качественное объяснение заключается в том, что молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда.          На основании использования основных положений молекулярно-кинетической теории было получено основное уравнение МКТ идеального газа,        которое выглядит так:  , где р — давление идеального газа, m0 — масса молекулы,  среднее значение   концентрация молекул, квадрата скорости молекул. Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа     получим основное уравнение     МКТ идеального газа в виде: 

7/11 Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнениеМенделеева — Клапейрона) — формула, устанавливающая зависимость междудавлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид: где

•  — давление,

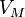•  — молярный объём,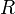

•  — универсальная газовая постоянная

•  — абсолютная температура,К.

Так как  , где   — количество вещества, а  , где   — масса,   —молярная масса, уравнение состояния можно записать:

7/13Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру   и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения   одинаково), барометрическая формула имеет следующий вид: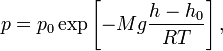 где   — давление газа в слое, расположенном на высоте  ,   — давление на нулевом уровне ( ),   — молярная масса газа,   — газовая постоянная,   — абсолютная температура. Из барометрической формулы следует, что концентрация молекул   (или плотность газа) убывает с высотой по тому же закону: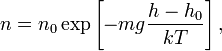 где   — масса молекулы газа,   — постоянная Больцмана

7/14Сравнивая уравнение состояния идеального газа и основное уравнение кинетической теории газов, записанные для одного моля (для этого число молекул N возьмём равным числу Авогадро N_А), найдём среднюю кинетическую энергию одной молекулы: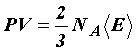  и  .

Откуда .        Средняя кинетическая энергия поступательного движения молекулы не зависит от её природы и пропорциональна абсолютной температуре газа T. Отсюда следует, что абсолютная температура является мерой средней кинетической энергии молекул.Величина R/N_А = k в уравнении (31) получила название постоянной Больцмана и представляет собой газовую постоянную, отнесенную к одной молекуле: k = 1,38·10^-23 Дж/К^-23. Так как 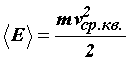 = kТ, то средняя квадратичная скорость равна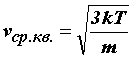 .           (32)

Подставляя значение средней кинетической энергии поступательного движения молекул в основное уравнение молекулярно–кинетической теории газов, получим другую форму уравнения состояния идеального газа:P = n₀kTДавление газа пропорционально произведению числа молекул в единице объема на его термодинамическую температуру.

7/16 Когда сталкиваются две субатомные частицы (например, α-частица и ядро золота в опыте Резерфорда), между ними может произойти взаимодействие, а может и не произойти. В последнем случае частицы сохраняют неизменными все свои характеристики. Мы не можем предсказать результат столкновения двух конкретных частиц, а лишь вероятность того или иного исхода столкновения. Таким образом, мы оперируем с вероятностями событий. Это вероятностное, а не строго определенное знание (или предсказание) того или иного события отличает физику микромира от физики классических объектов.      Основной величиной, которой оперируют физики, исследующие столкновение микрообъектов, является эффективное сечение или просто сечение (более полное название поперечное эффективное сечение). Именно эта величина определяет вероятность того или иного результата столкновения.

7/17 Длина свободного пробега молекулы — это среднее расстояние (обозначаемое  ), которое частица пролетает за время свободного пробега от одного столкновения до следующего.

Длина свободного пробега каждой молекулы различна, поэтому в кинетической теории вводится понятие средней длины свободного пробега (<λ>). Величина <λ> является характеристикой всей совокупности молекул газа при заданных значенияхдавления и температуры.

, где   — эффективное сечение молекулы,   — концентрация молекул.

8/1 В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна

Так как в одном киломоле содержится   молекул, то внутренняя энергия одного киломоля газа будет Учитывая,что   ,получим Для любой массы m газа, т.е. для любого числа киломолей   внутренняя энергия Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю. Математически это записывается в виде тождества

8/2 Механическая работа определяется как: ,где   — сила, а   — элементарное (бесконечно малое) перемещение.

Элементарная работа термодинамической системы над внешней средой может быть вычислена так:

, где   — нормаль элементарной (бесконечно малой) площадки,   — давление и   — бесконечно малое приращение объёма.

Работа в термодинамическом процессе  , таким образом, выражается так: .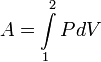

Величина работы зависит от пути, по которому термодинамическая система переходит из состояния   в состояние  , и не является функцией состояния системы. Такие величины называют функциями процесса.

8/3 Коли́чество теплоты́ — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основных термодинамических величин.Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.Единица измерения: Джоуль Дж

Рассмотрим систему, состоящую из двух тел   и  . Предположим, что тело   заключено почти полностью в жёсткую адиабатическую оболочку, так что оно не способно совершатьмакроскопическую работу, а обмениваться теплом (то есть энергией) посредством микроскопических процессов может лишь с телом  . Предположим, что тело   также заключено в адиабатическую оболочку почти полностью, так что для него возможен теплообмен лишь с  , но не будем предполагать, что оболочка жёсткая. Количеством теплоты, сообщённой телу   в некотором процессе, будем называть величину  , где   — изменение внутренней энергии тела  . Согласно закону сохранения энергии,

где   — макроскопическая работа внешних сил над телом  . Если учесть, что

где   — работа, совершённая телом  , то закону сохранения энергии можно придать форму первого начала термодинамики:

Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела   и способа теплообмена между телами. Заметим, что для определения количества теплоты необходимо пробное тело, в противном случае первое начало теряет смысл содержательного закона и превращается в определение количества теплоты (весьма бесполезное в таком виде). При определении количества теплоты независимо от   и   первое начало становится содержательным законом, допускающим экспериментальную проверку.

Отметим, что, как и совершённая работа, количество переданной теплоты зависит от конкретного процесса, совершённого над телом.

8/4 еплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT: Единица измерения теплоёмкости в системе СИ — Дж/К.

Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. В молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с iстепенями свободы при постоянном объёме (для одного моля идеального газа) равна:

где R ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная.

А при постоянном давлении

8/5 Теорема о равнораспределении кинетической энергии по степеням свободы, закон равнораспределения, теорема о равнораспределении — связывает температуру системы с её среднейэнергией в классической статистической механике. В первоначальном виде теорема утверждала, что при тепловом равновесии энергия разделена одинаково между её различными формами, например, средняя кинетическая энергия поступательного движения молекулы должна равняться средней кинетической энергии её вращательного движения. С помощью теоремы о равнораспределении можно делать количественные предсказания. Как и вириальная теорема, она даёт полные средние кинетические и потенциальные энергии для системы при данной температуре, из которых можно вычислить теплоёмкость системы. Однако теорема о равнораспределении также позволяет определить средние значенияотдельных компонентов энергии, такие как кинетическая энергия одной частицы или потенциальная энергия отдельной пружины. В теореме утверждается, что каждая молекула в идеальном газе обладает средней кинетической энергией равной (3/2)k_BT при термодинамическом равновесии, где k_B — постоянная Больцмана, T — температура. В общем случае её можно применять к любой классической системе, находящейся в состояниитеплового равновесия, независимо от того, насколько она сложна

8/6 В любой изолированной системе запас энергии остаётся постоянным.^[2] Это — формулировка Дж. П. Джоуля (1842 г.).Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних силИзменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики^[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется. Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты  , сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества   при химическом потенциале  , и работы  ^[3], совершённой над системой внешними силами и полями, за вычетом работы  , совершённой самой системой против внешних сил .Для элементарного количества теплоты  , элементарной работы   и малого приращения   внутренней энергии первый закон термодинамики имеет вид: .Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.

Важно заметить, что   и   являются полными дифференциалами, а   и   — нет.

8/7 Обратимым процессом называют такой процесс, который может быть проведен в обратном направлении таким образом, что система будет проходить через те же состояния, что и при прямом ходе, но в обратной последовательности. Обратимым может быть только равновесный процесс.

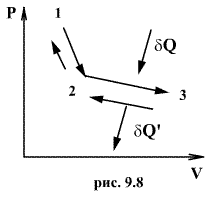
Обратимый процесс обладает следующими свойствами: если при прямом ходе на каком-то элементарном участке (рис. 9.8.) система получает тепло   и совершает работу   , то при обратном ходе на том же участке система отдает тепло   и над ней совершается работа  . По этой причине после протекания обратимого процесса в одном, а затем в обратном направлении и возвращение системы в первоначальное состояние в окружающих телах не должно оставаться никаких изменений. Например шарик на пружине в вакууме колеблется бесконечно долго.

В том случае, когда после завершения прямого и обратного процессов система вернулась в первоначальное состояние и в окружающей среде остались изменения, процесс является необратимым. Очевидно, что все процессы в природе необратимые.