
- •Содержание
- •Введение.
- •§1. Основные определения и понятия.
- •§2. Классификация игр.
- •§3. Игра двух сторон с нулевой суммой.
- •§4. Графическое решение игры 2×2.
- •§5. Упрощение игры.
- •§6. Решение игр вида 2×n и m×2.
- •§7. Сведение игры двух лиц с нулевой суммой к линейной распределительной задаче.
- •Упражнения.
- •Литература.
Упражнения.
№1. Определить нижнюю и верхнюю цены игры
а)
![]() б)
б)
![]()
Ответы: а) α=3; β=3 б) α=2; β=4; 2≤V≤4
.
.
№2. Найти седловую точку и цену игры по платежной матрице и определить оптимальные чистые стратегии
а) .
б)
.
б)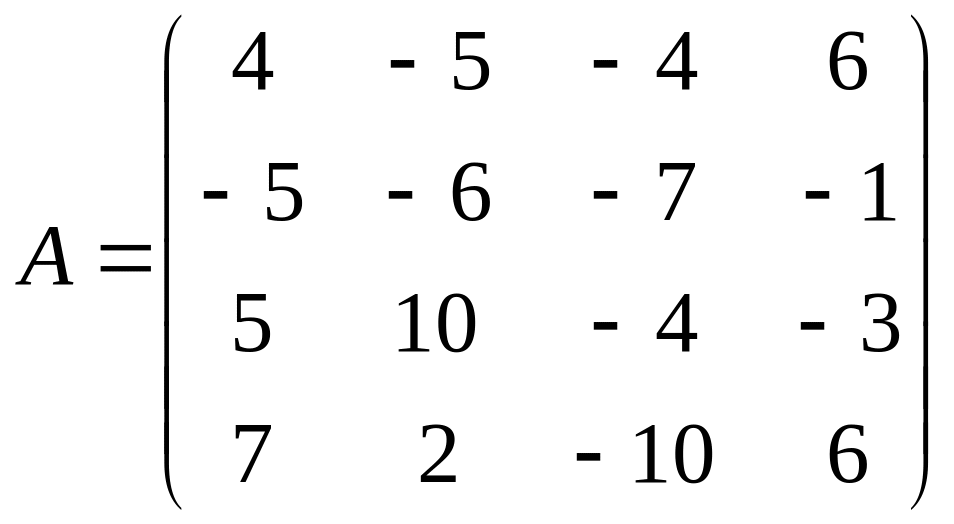
Ответы: а) α=β=V=4;(А2В3) б) α=β=V=-3 (А3В4)
№3. 1) Каждый из двух партнеров, не зная хода другого, кладет свою монету орлом или решкой вверх и при совпадении наименований второй игрок платит первому одну денежную единицу, а при несовпадение первый платит второму столько же.
Составить платежную матрицу и решить игру.
2) Цех заготовитель поставляет в сборочный цех детали двух видов а и в. По договору между цехами оговорены ежедневно два срока поставок этих деталей, причем, при поставке в первый срок деталей вида ,,а” сборочный цех платит заготовительному премию 60 руб., при поставке же изделий ,,а” во второй срок выплачивается премия 20 руб. При поставке же изделий вида ,,в” в первый срок премия составляет 40 руб., а во второй 50 руб. Определить оптимальные стратегии поставок и получения деталей и размер премии.
Ответы:
1)![]()
![]() 2)
2)![]()
![]()
№4. Найти нижнюю и верхнюю цены игры, определить наличие Седловой точки и чистые стратегии, если они есть
а)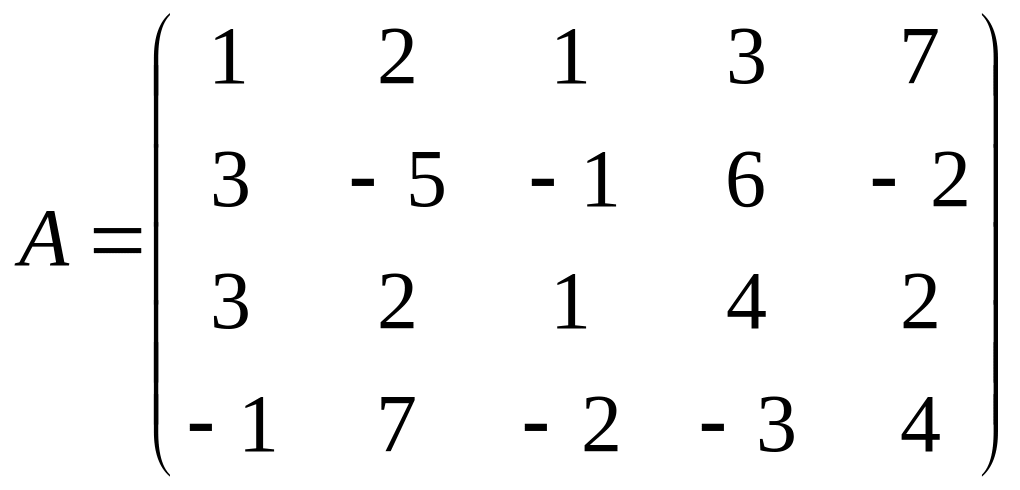 ;
б)
;
б)
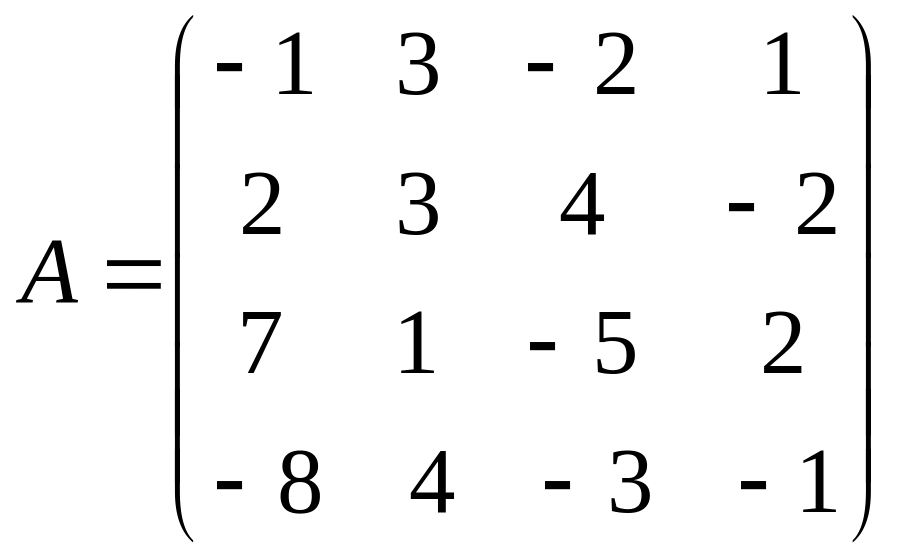
Ответы а) α=β=V=1; б) α=-2; β=2. -2≤V≤2; (А1 В3) и (А3 В3).
№5. Определить область значений х, для которых стратегия А2 и В2 будут оптимальными в следующих играх
а)
 ,
б)
,
б)
 ,
в)
,
в)
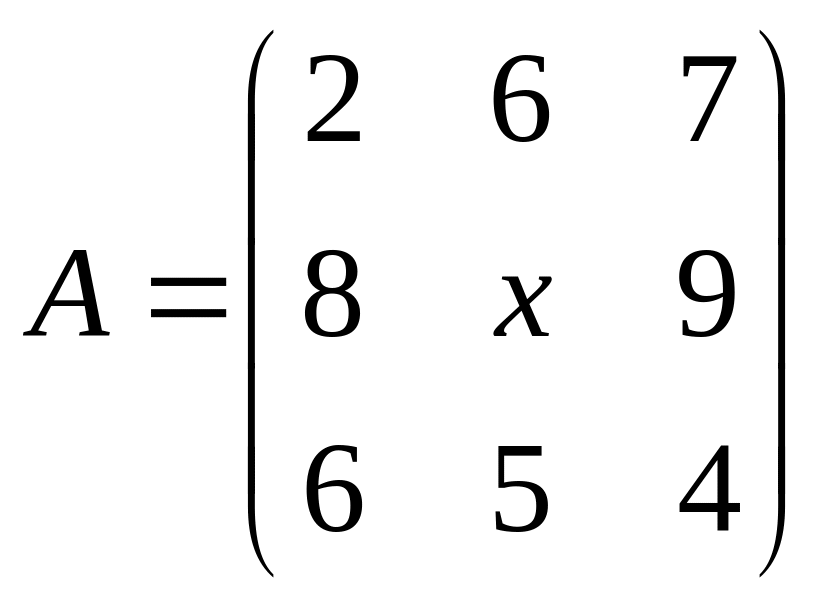 .
.
Ответы: а) 4≤х≤5; б) 3≤х≤7; в) 4≤х≤6.
№6. Определить будут ли значения цены следующих игр больше, меньше или равны нулю:
а)
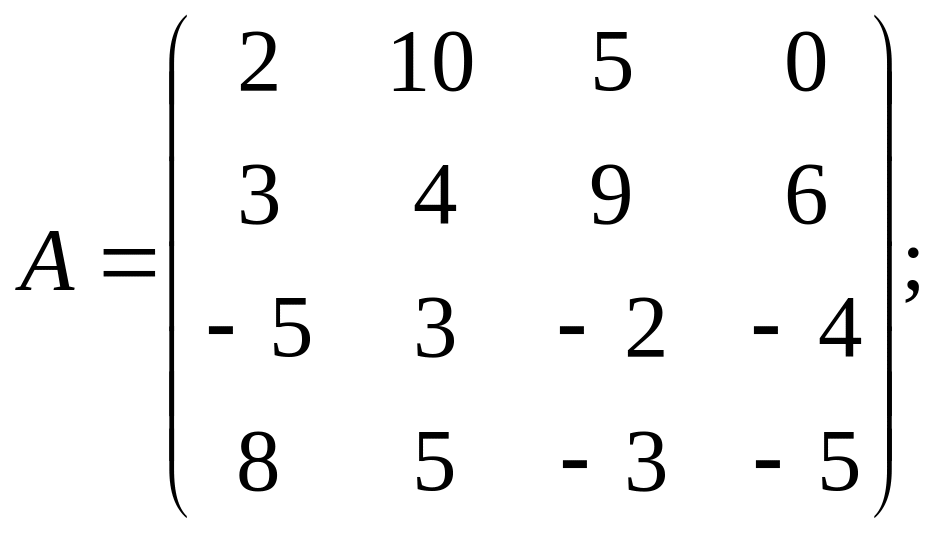 б)
б)
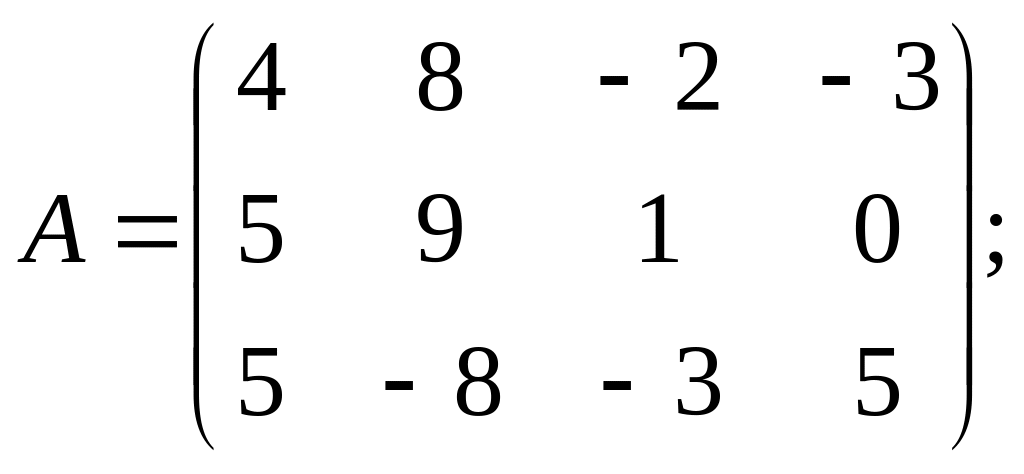 в)
в)
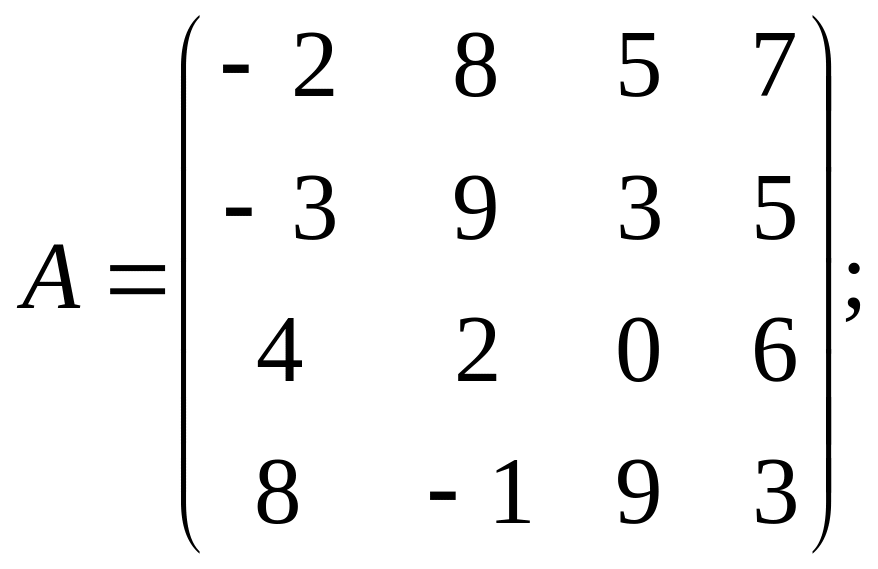
г)
 .
.
Ответы: а) V>0; б) V≥0; в) V≥0; г) V>0.
№7. Швейное предприятие выпускает детские костюмы, платья и плащи. Сбыт этих товаров зависит от состояния погоды. По статистическим данным полученным за предыдущие годы, предприятие в течении апреля – мая в условиях теплой погоды может реализовать 600 костюмов, 2000 платьев и 300 плащей, в условиях прохладной погоды – 1000 костюмов, 500 платьев и 800 плащей и в условиях обычной погоды 800 костюмов, 1100 платьев и 600 плащей. Затраты на единицу продукции в течении указанных месяцев составили для костюмов 30 ден. ед., для платьев 10 ден. ед. и для плащей 15 ден. ед., а цена реализации равна соответственно 50 ден. ед., а цена реализации равна соответственно 50 ден. ед., 20 ден. ед., 28 ден. ед.
Необходимо максимизировать среднюю величину прибыли от реализации выпущенной продукции с учетом неопределенности погоды в рассматриваемые месяцы. Для этого необходимо составить платёжную матрицу, пару двойственных задач линейного программирования и решить симплексным методом.
Ответ: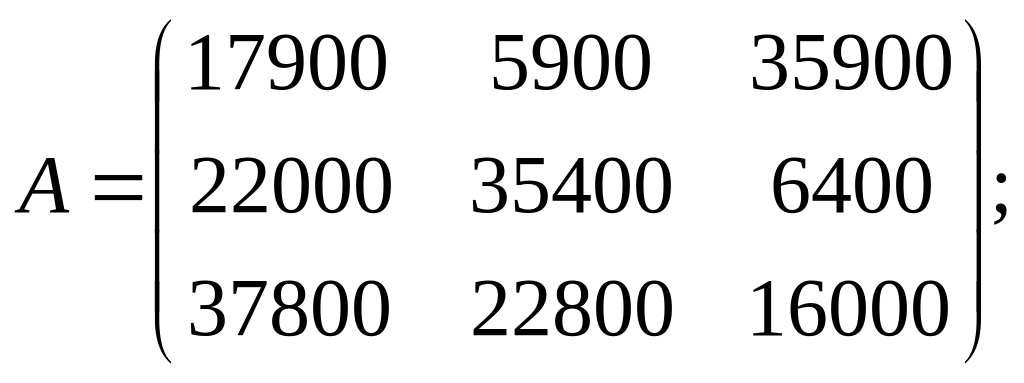
![]()
![]() .
.
![]()
№8. Упростить игру, заданную матрицей и решить
а)
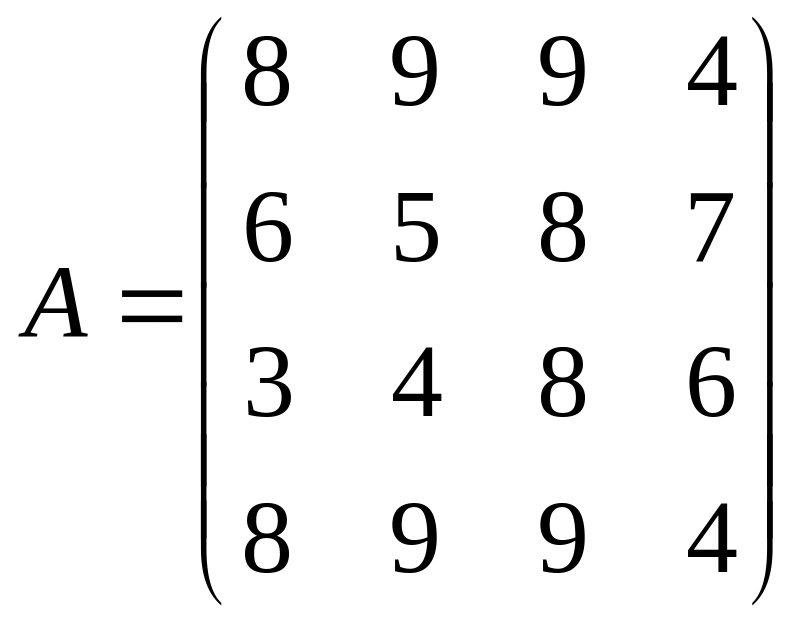 ;
б)
;
б)
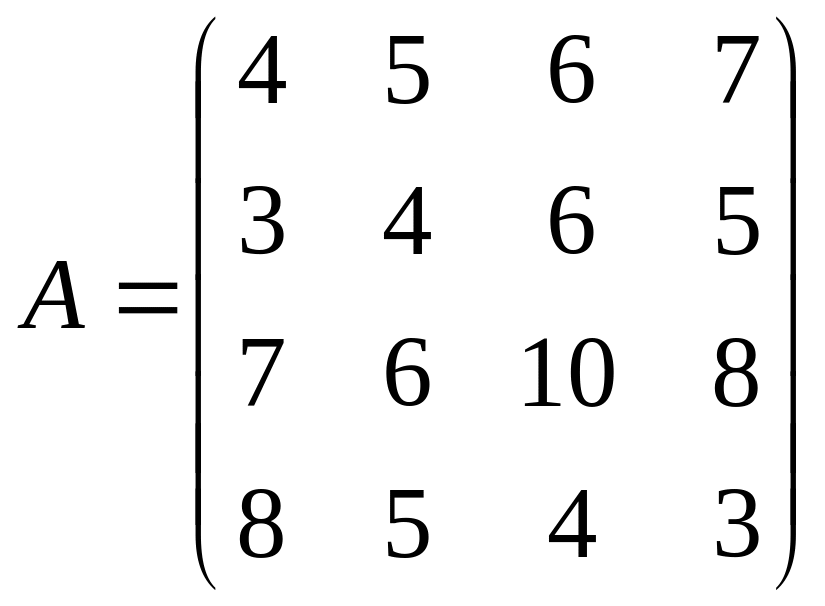 ;
в)
;
в)
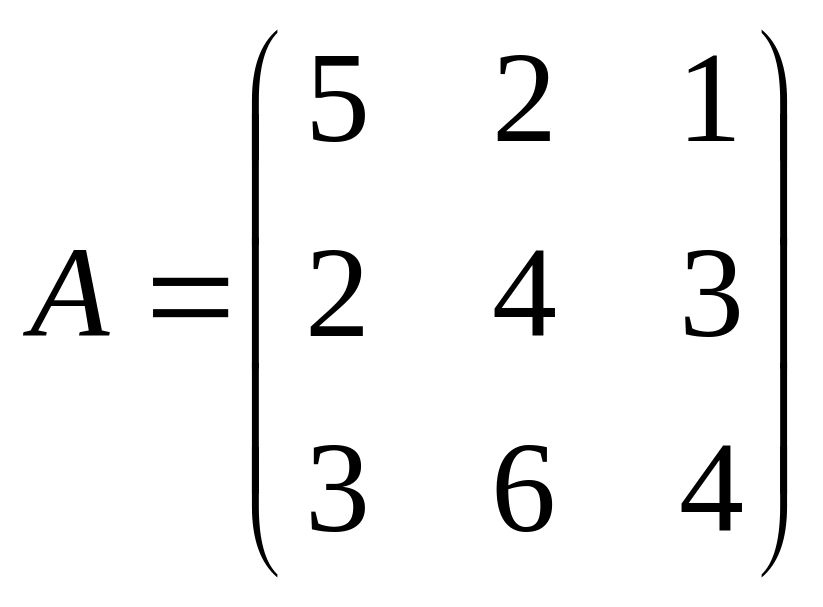 ;
г)
;
г)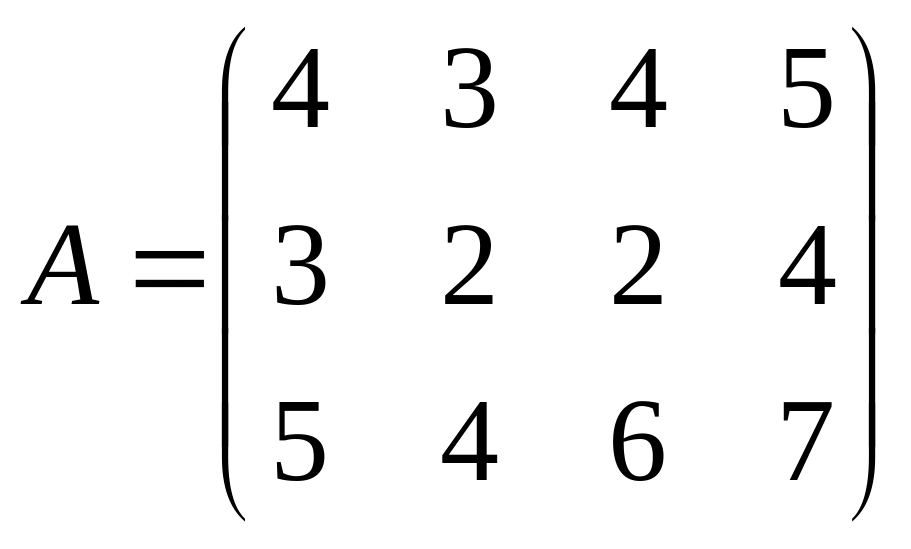
№9. Предположим, что предприятие может выпускать четыре вида продукции: А1, А2, А3, А4 получая при этом прибыль. Её величина определяется состоянием спроса, который может находиться в одной из трёх возможных состояний: В1, В2, В3.
Прибыль предприятия при различных состояниях спроса задана матрицей
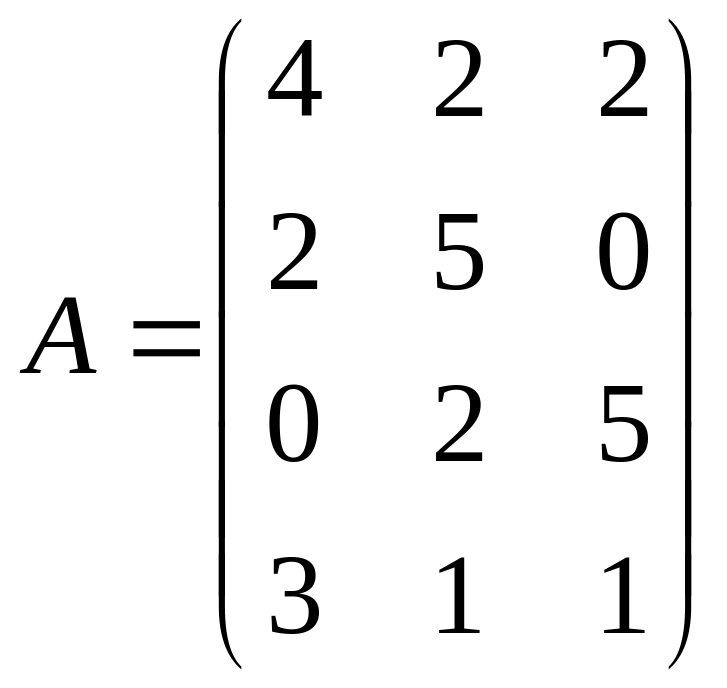
Необходимо определить оптимальные пропорции выпускаемых предприятием видов продукции, продажа которой обеспечила бы ему максимально возможную выручку от состояния спроса.
Ответ:
![]() V>2,5мл.руб.
V>2,5мл.руб.
![]()
№10.Планирование посевов Фермер, имеющий ограниченный участок земли может засадить его тремя различными культурами А1, А2, А3. Урожай этих культур зависит главным образом от погоды, которая может находиться также в трёх различных состояниях: В1, В2, В3. Фермер имеет информацию об урожайности этих культур при трех различных состояниях погоды, которая отражена в таблице
-
Засуха
Нормальная
Дождливая
Цена Сi
В1
В2
В3
А1
20
5
15
2
А2
7,5
12,5
5
4
А3
0
7,5
10
8
аij - количество центнеров культуры с гектара
сi – рыночная цена одного центнера культуры Аi
Составить матрицу доходов от продажи культур и определить пропорции, в которых фермер должен засеять имеющийся участок земли, чтобы максимизировать свой доход, независимо от погодных условий.
Ответ: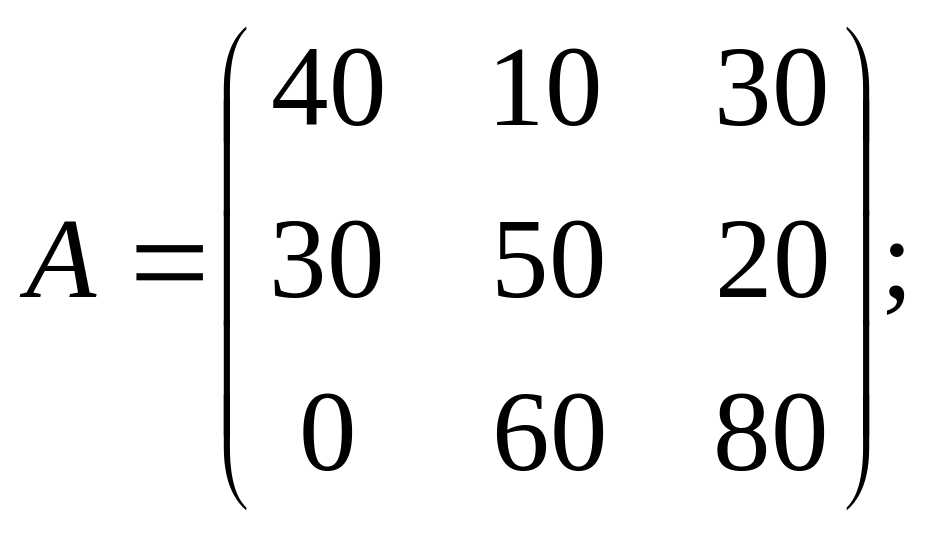
![]()
![]() V=31,5тыс.руб
V=31,5тыс.руб
№11. Решить игру:
1)![]() ;
2)
;
2)![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() 6)
6)![]() ;
7)
;
7)
![]() .
.
Ответы:
1)![]() ,
,
![]() 2)
2)
![]() ,
,
![]()
3)![]()
![]() 4)
4)
![]()
![]()
5)![]()
6)![]()
7)
![]()
№12. Магазин может завести в различных пропорциях товары четырёх типов (А1,А2,А3,А4). Их реализация и прибыль магазина зависят от вида товара и состояния спроса. Предполагается, что спрос может иметь пять состояний (В1,В2,В3,В4,В5) и не прогнозируются. Определить оптимальные пропорции в закупке товаров из условия максимизации средней гарантированной прибыли следующей матрице прибыли.
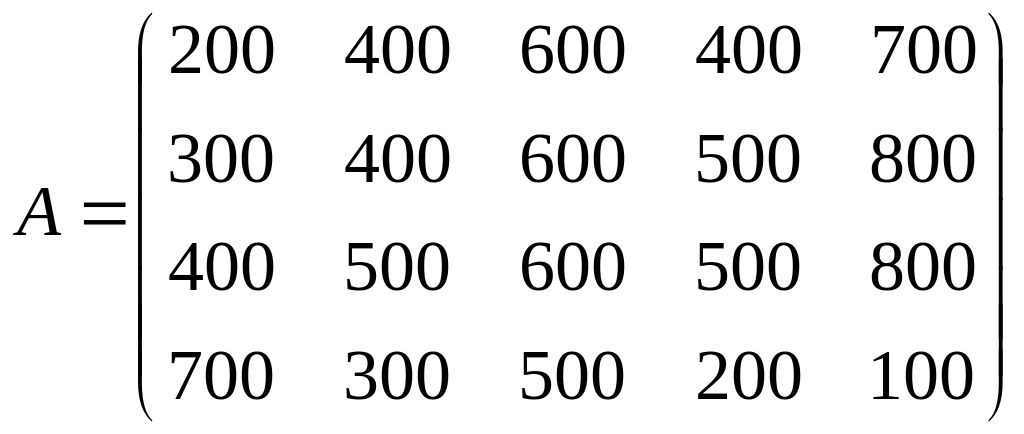
Ответ:
![]()
№13.Предполагается оснастить цех новой технологической линией. Промышленность выпускает три типа линий. На каждой из линий можно изготовлять пять различных видов изделий. Учитывая расход сырья, трудоемкость, спрос и др., составлена матрица предполагаемой прибыли.
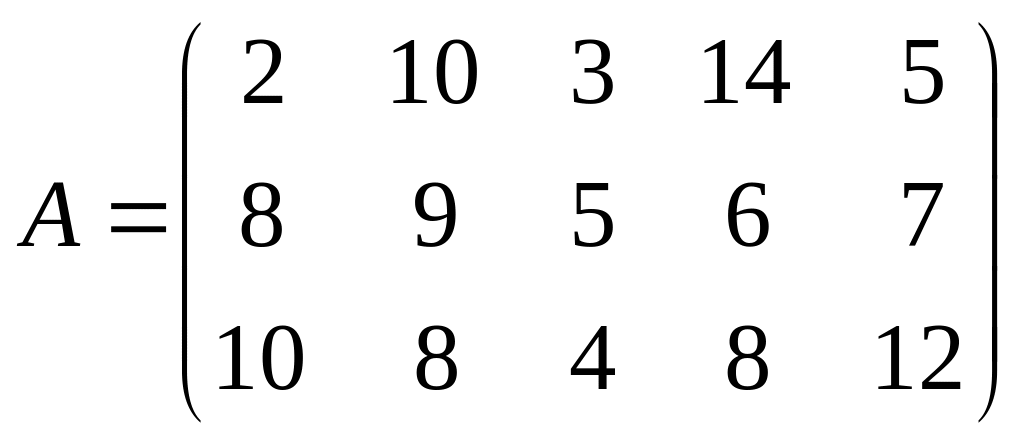
Нужно выбрать тип технологической линии, при которой прибыль будет наибольшей.
Ответ: α=β=v=5; (A2;B3).
№14.Предприятие выпускает два вида скоропортящихся продуктов А и В. Себестоимость единицы А составляет 8 руб., а отпускная цена 12 руб. Себестоимость единицы В 5 руб., отпускная цена 8 руб. Если продукция не реализуется в день выпуска, то её качество резко снижается и она продаётся на следующий день по цене в четыре раза нижеотпускной. Реализация продукции зависит от погоды: в хорошую погоду реализуется 2500 ед. продукции A и 15000 ед. продукции B, а в плохую 10000ед продукции A и 3000 ед. продукции В. На реализацию всей продукции в день расходуется 5000 руб. Определить ежедневное производство каждого вида с целью получения наибольшей прибыли.
Ответ:
Платежная матрица имеет вид
![]() ,
,
![]()
![]() -объемы
реализации.
-объемы
реализации.
№15. Решить игру.
1)
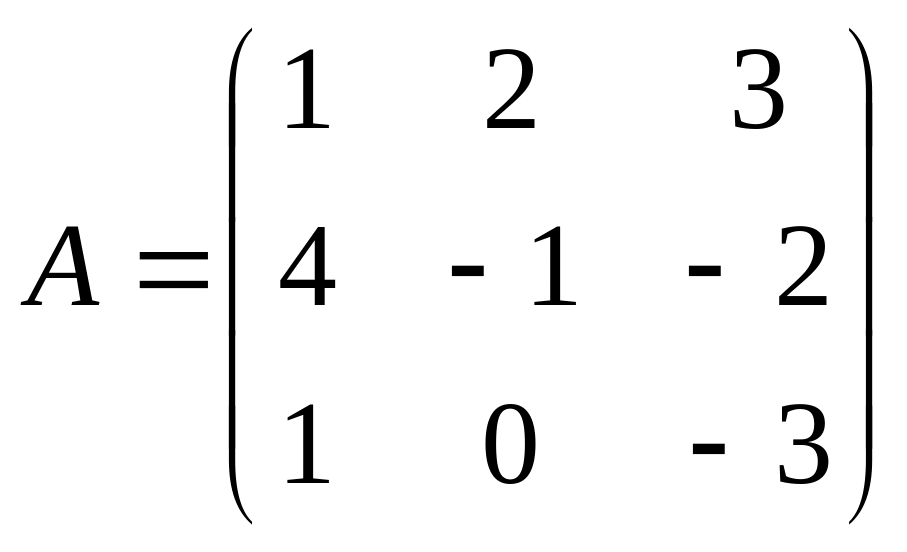 ;
2)
;
2)
 ;
3)
;
3)
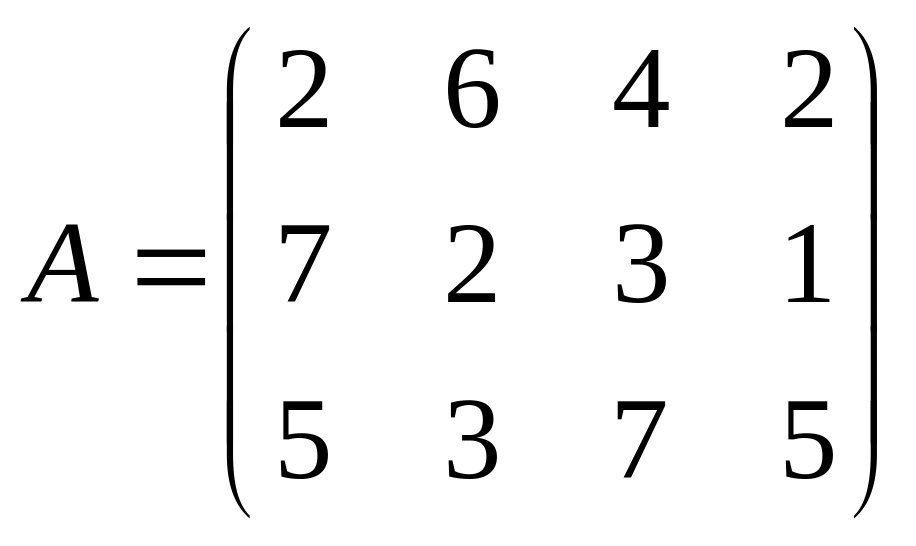 ;
;
4)
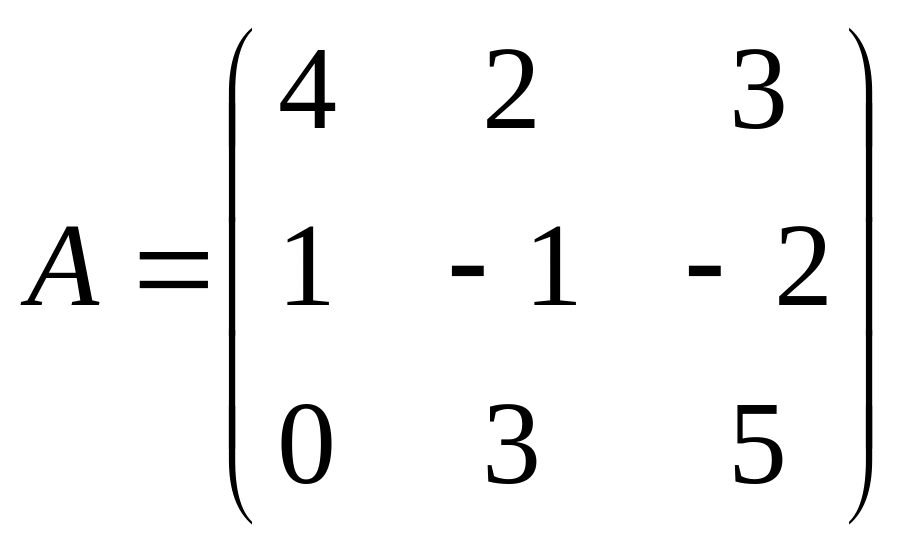 ;
5)
;
5) ;
6)
;
6)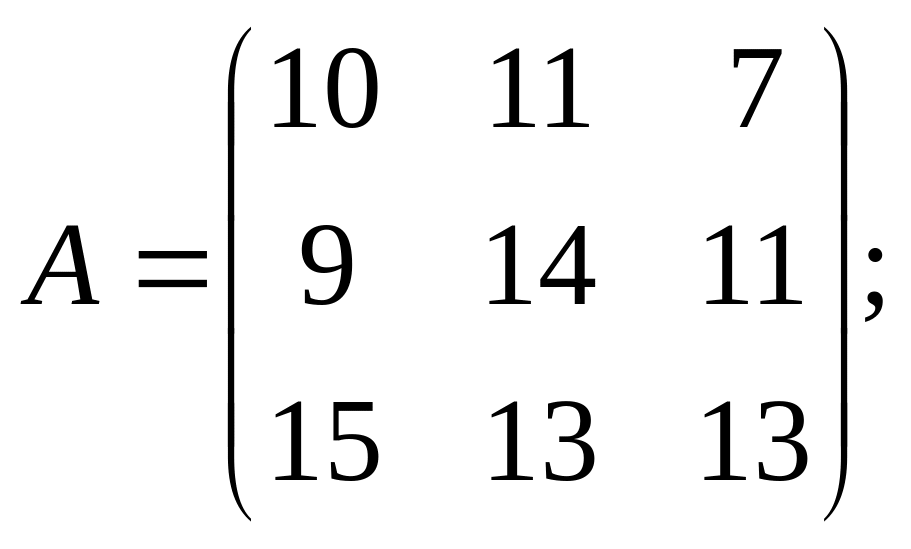
7) ;
8)
;
8)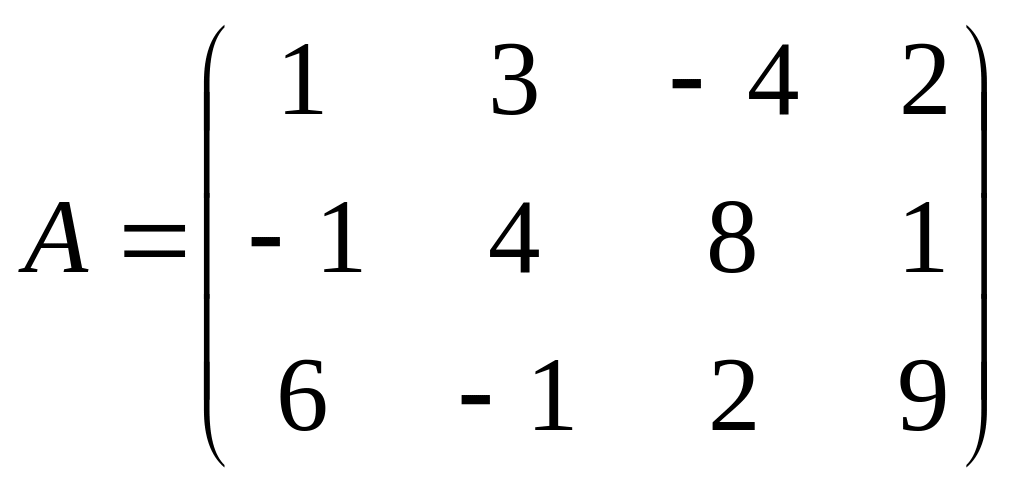 ;
9)
;
9) ;
10)
;
10)![]() ;
11)
;
11)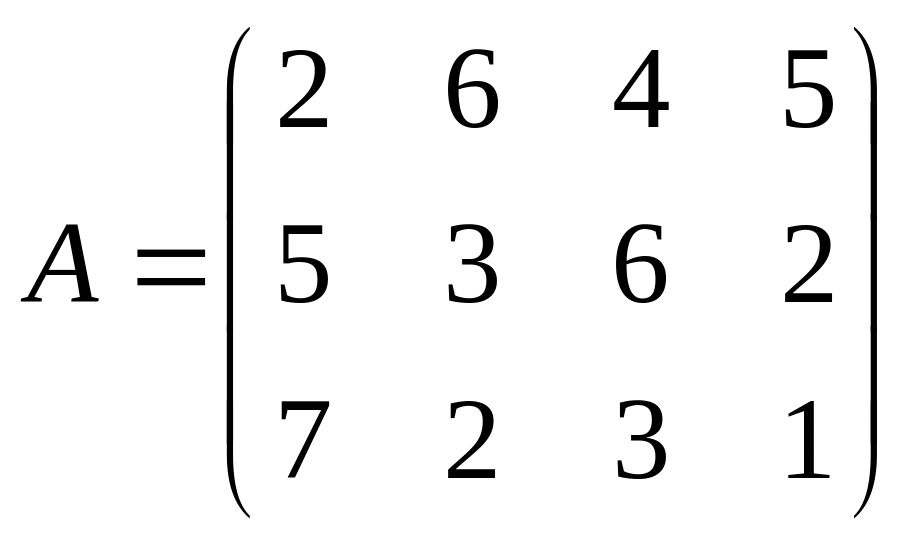 ;
12)
;
12)
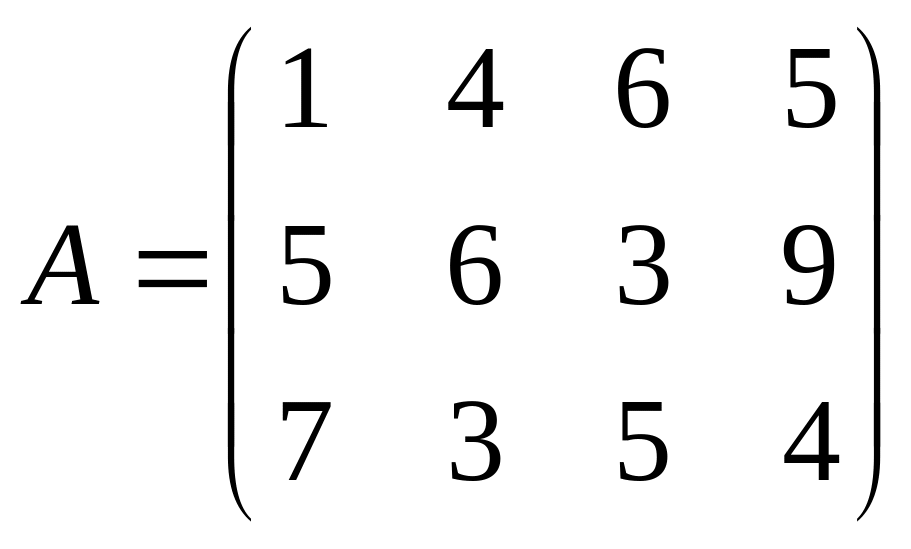 ;
13)
;
13)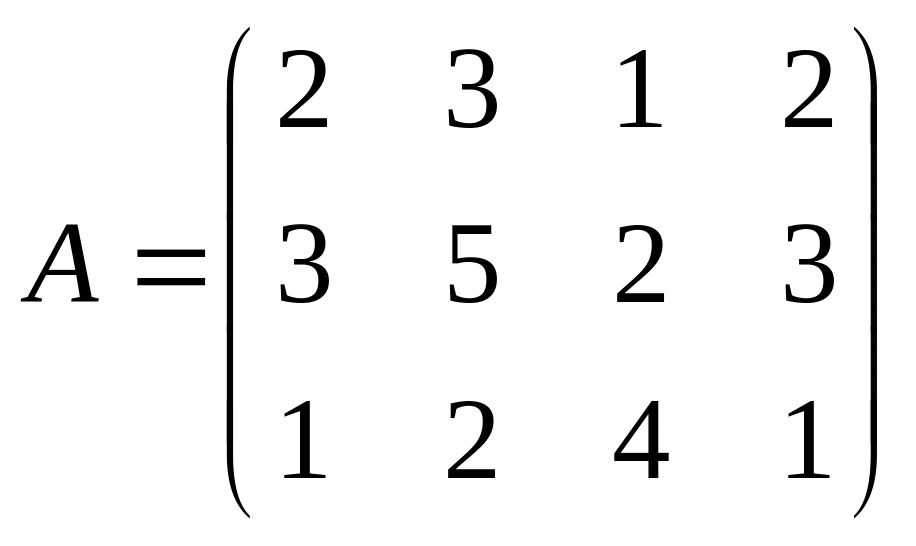 ;
14)
;
14)
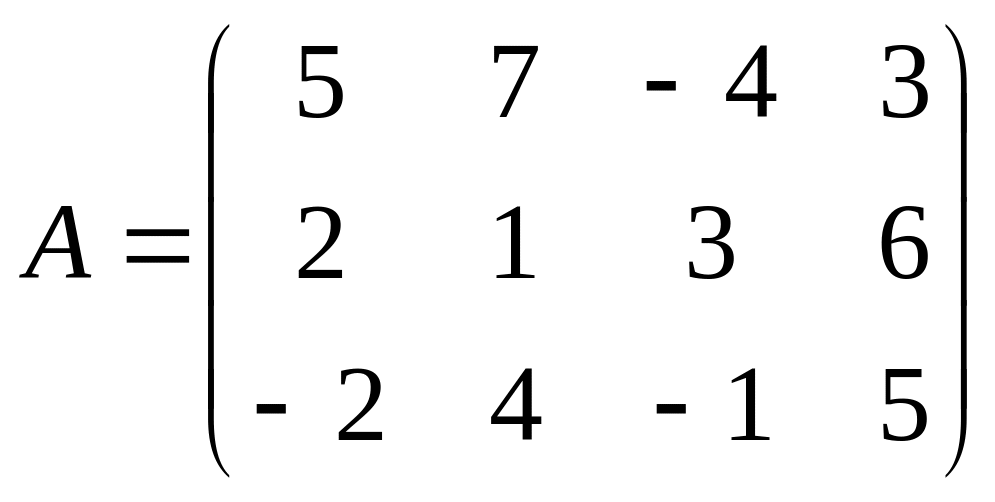 ;
15)
;
15)
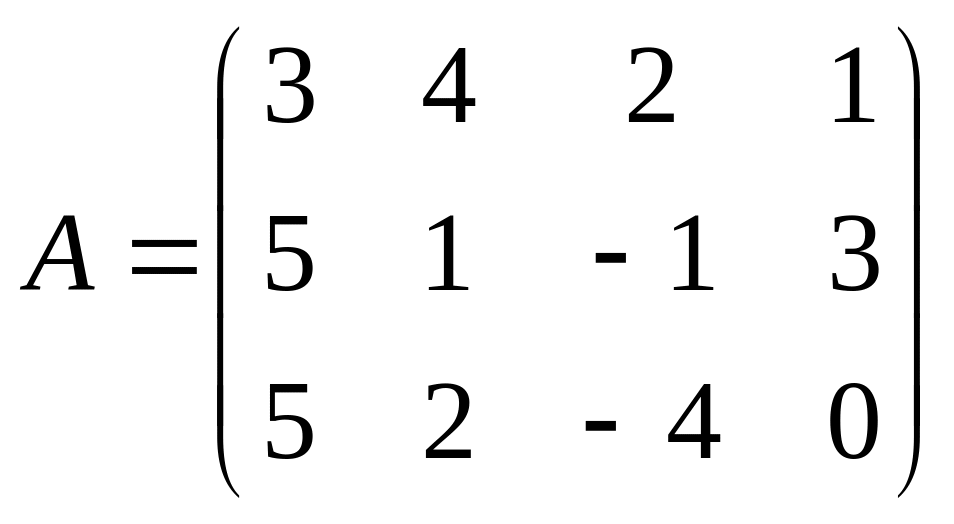 .
.
Ответы:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
