17.Первый закон Ньютона, инерциальные со

Если тело не подвергается внеш воздействиям, то оно либо покоитлся, либо движется равномерно прямолинейно.

Выбор Со

Если в какой либо СО тело равномерно прямолинейно движетс то в др Со движется с ускорением относительно 1, не будет двигаться равномерно прямолинейно. Следует что законб Ньютона справедливы только в инрециальных СО.

Содержание закона сводится к утверждению что существует покрайнимере одна СО в котором справедлив 1 закон.

18.Второй закон.

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение: F=ma

Если F/=0 то точка движется

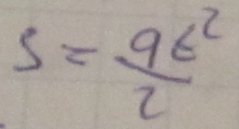
F=dp/dt при v<<с, при v<=с, p=mv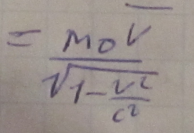 F=ma=md^2r/dt^2 a=dv/dt=d^2r/dt^2

19. 3 Закон Ньютона

При взаимодействии 2 тел, каждое из них дейсвует друг на друга с одинаковой по значению, но противоположной по направлению силой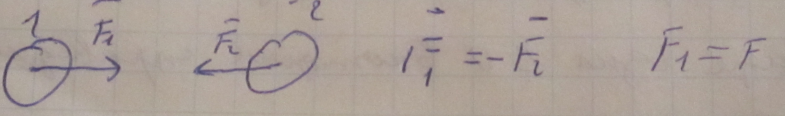

Не всегда выполняется и в частности при эл.магнитном взаимодействии, движущихся эл. Зарядов.

Закон заключается в сохранение импульсов взаимодейств тел, если на эти тела не действует внеш сила.

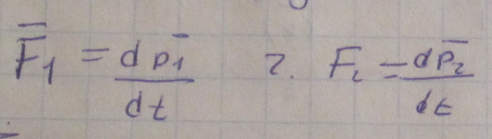
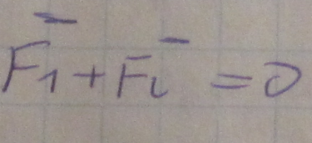
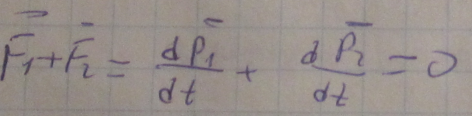
20.Момент инерции м.Т, системы м.Т, тв.Тела. Относительно оси

Момент инерции- динамический параметр при вращательном движение (при поступ).

1. М.т. y=mr^2 r- от точки до оси.

2. Система м.т.

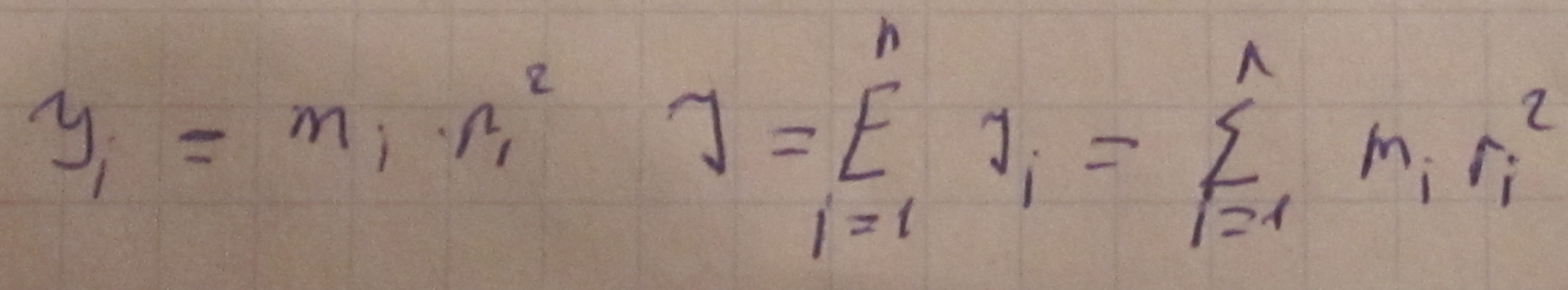
3. Момент инерции тв. Тела.

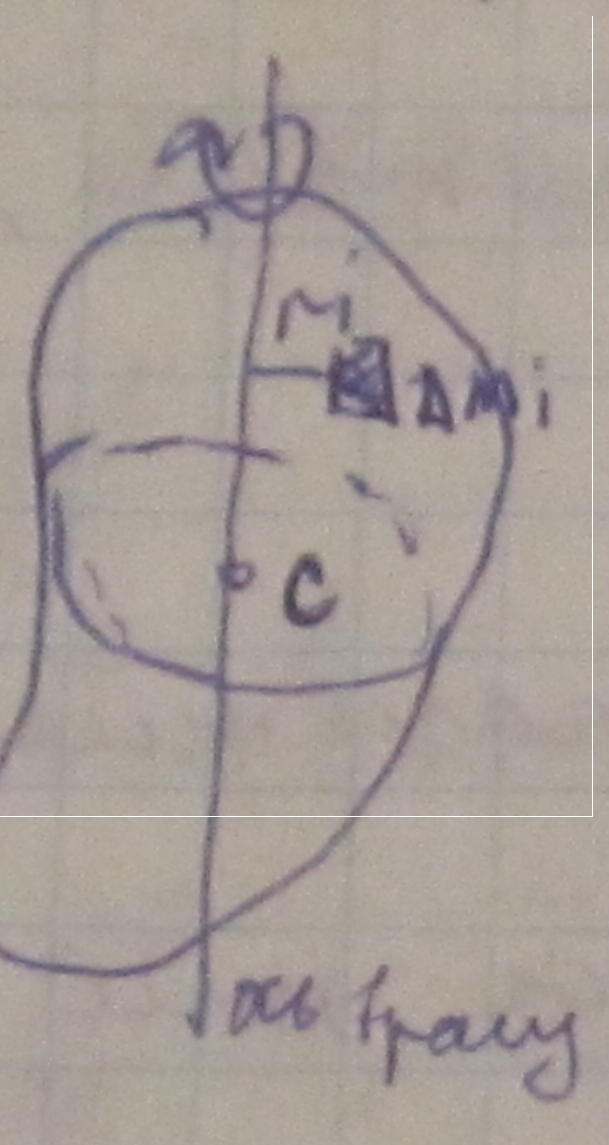
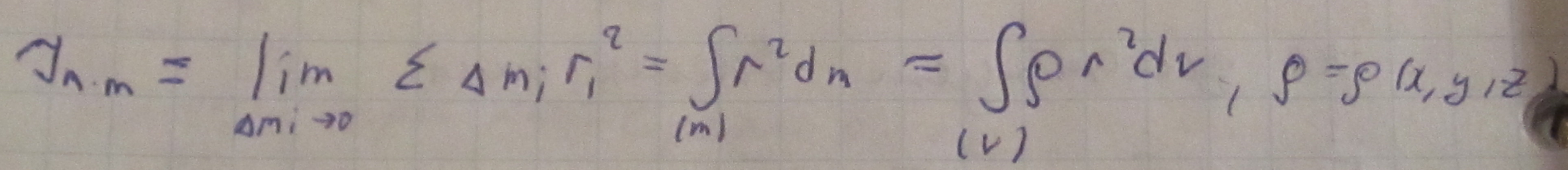
Пример-

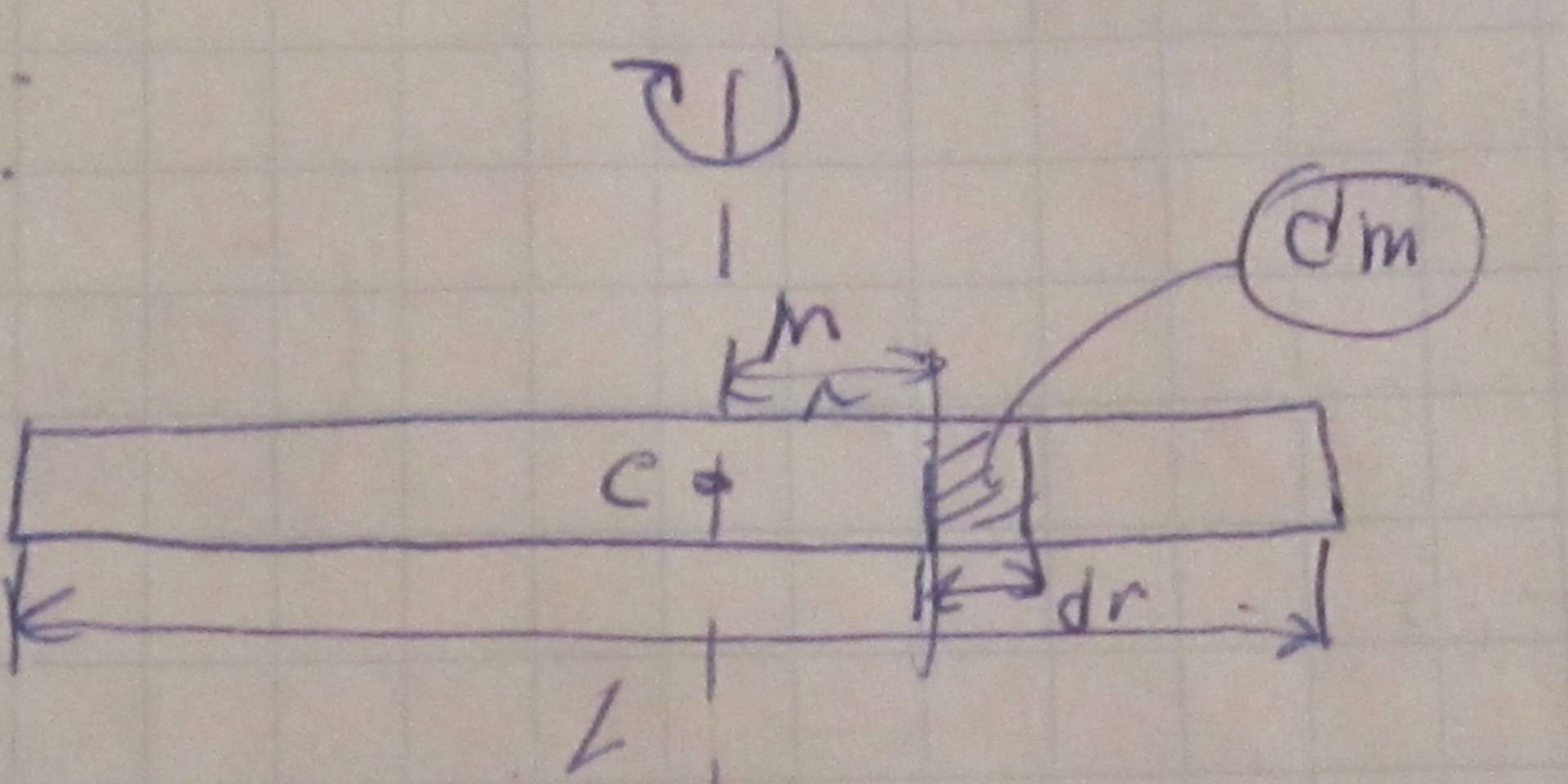
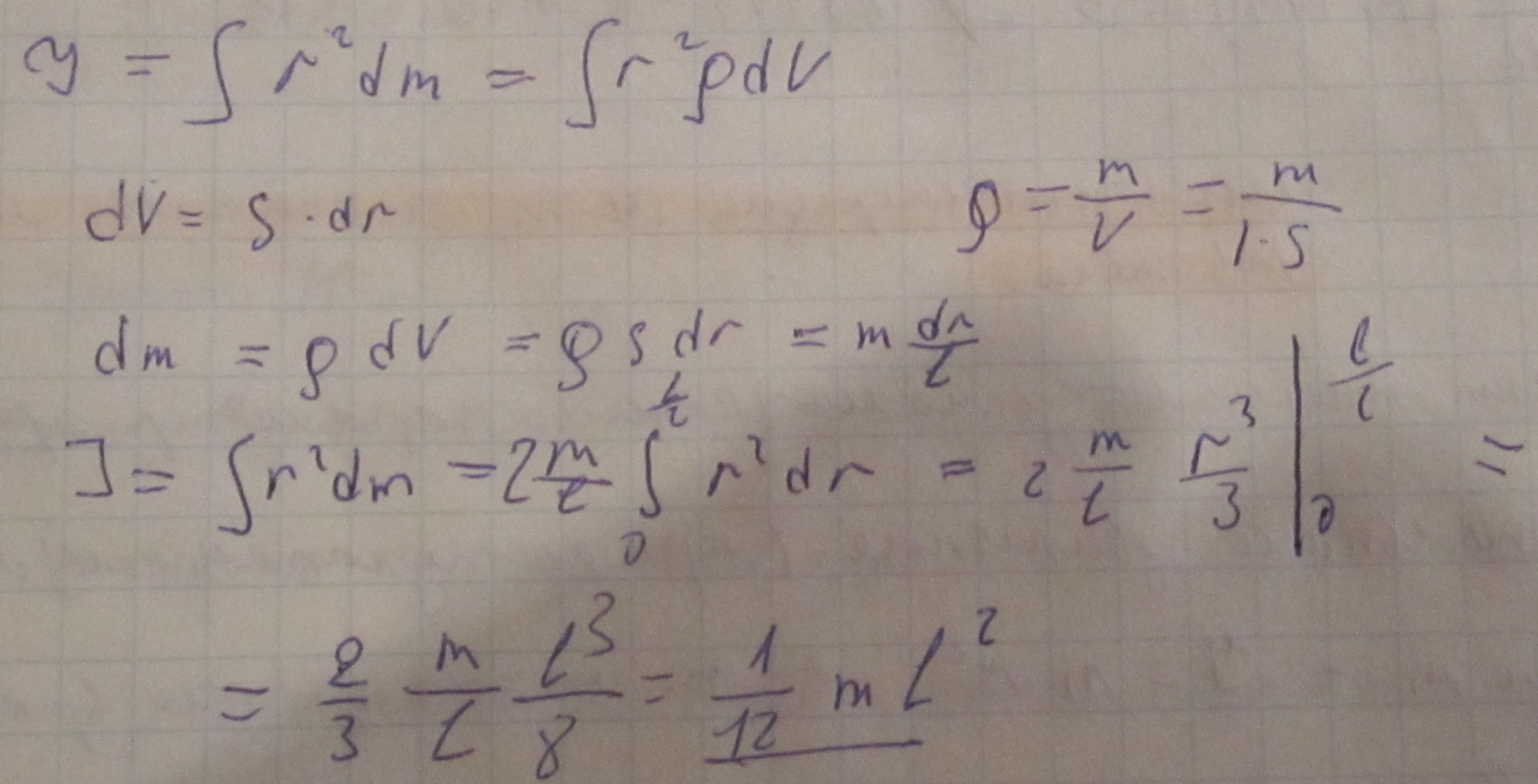
21.Св-во момента инерции, тв тела относ оси, теорема штейнера.

1. Аддитивность момента инерции.

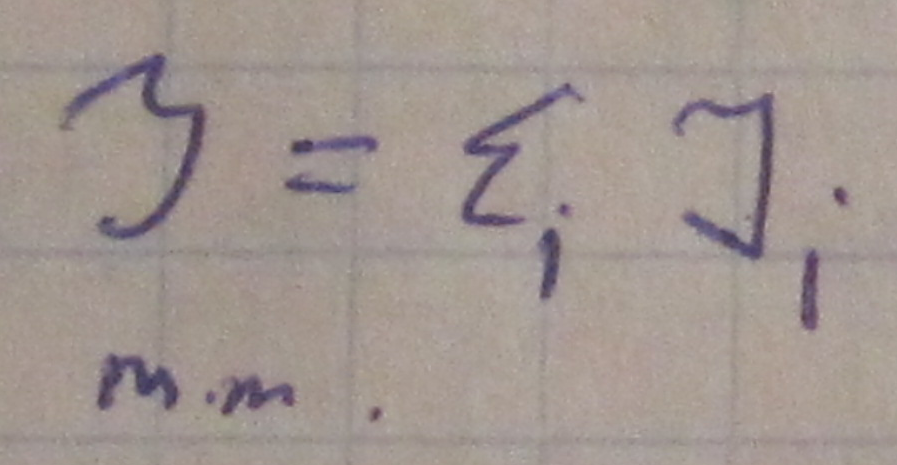
2. Момент инерции тела зависит от выбора оси, вокруг которой вращаяется тело.

3. Теорема Штейнера.

Момент инерции тела вокруг произвольной оси не проходящий через центр масс равен сумме момента инерции тела относительно осей проходящих через центр масс и произведения массы тела на квадрат расстояния между осями.

Y=Yc+ma^2 a –расстояние, с- центр масс.

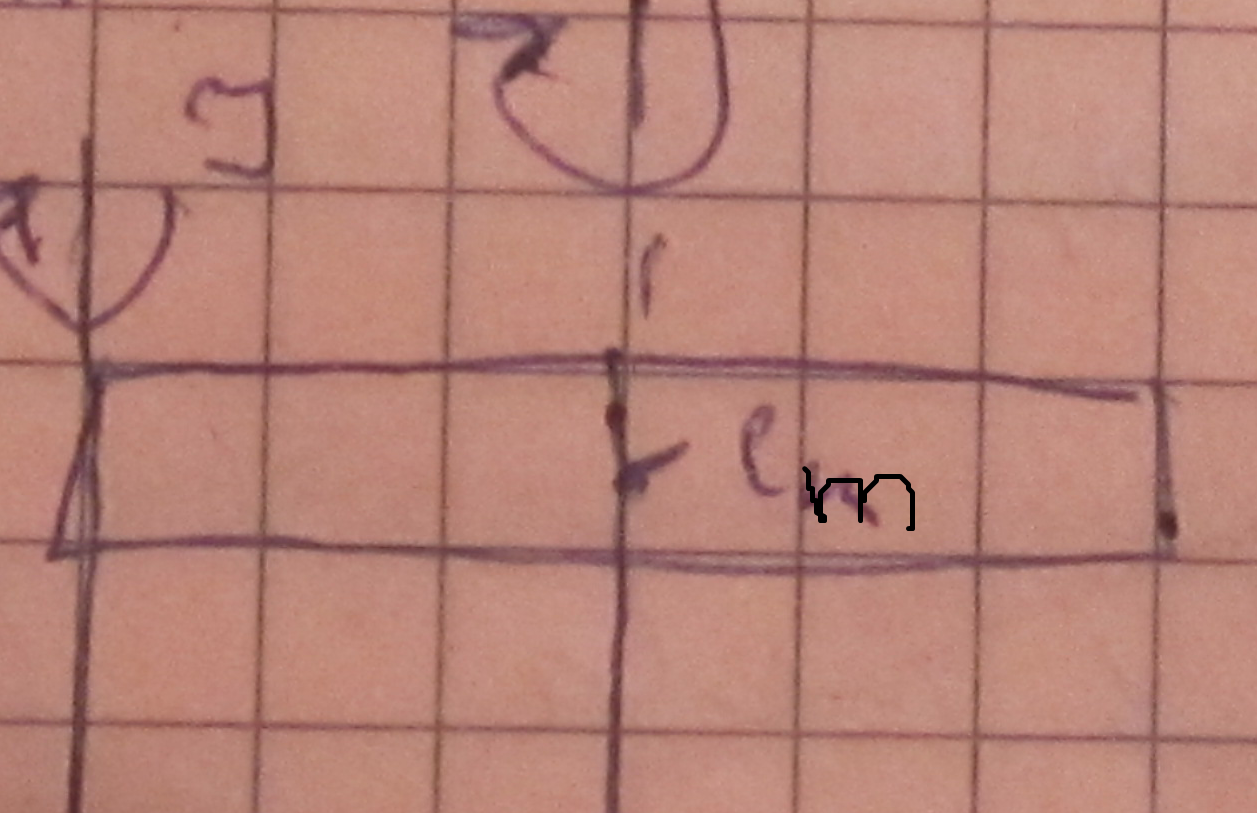, а=L/2

22.Главные и свободные оси инерции тела, Главный момент инерции, устойчивые оси вращения.

4. Главные оси инерции – 3 взаимно перпендикулярные оси координат относительно которых моменты инерции отличны от нуля. Эти моменты инерции называются главными моментами инерции тела. (Yx,Yy,Yz)

Если главные оси инерции проходят через центр масс тела, то эти оси называются центральными главными осями инерции.

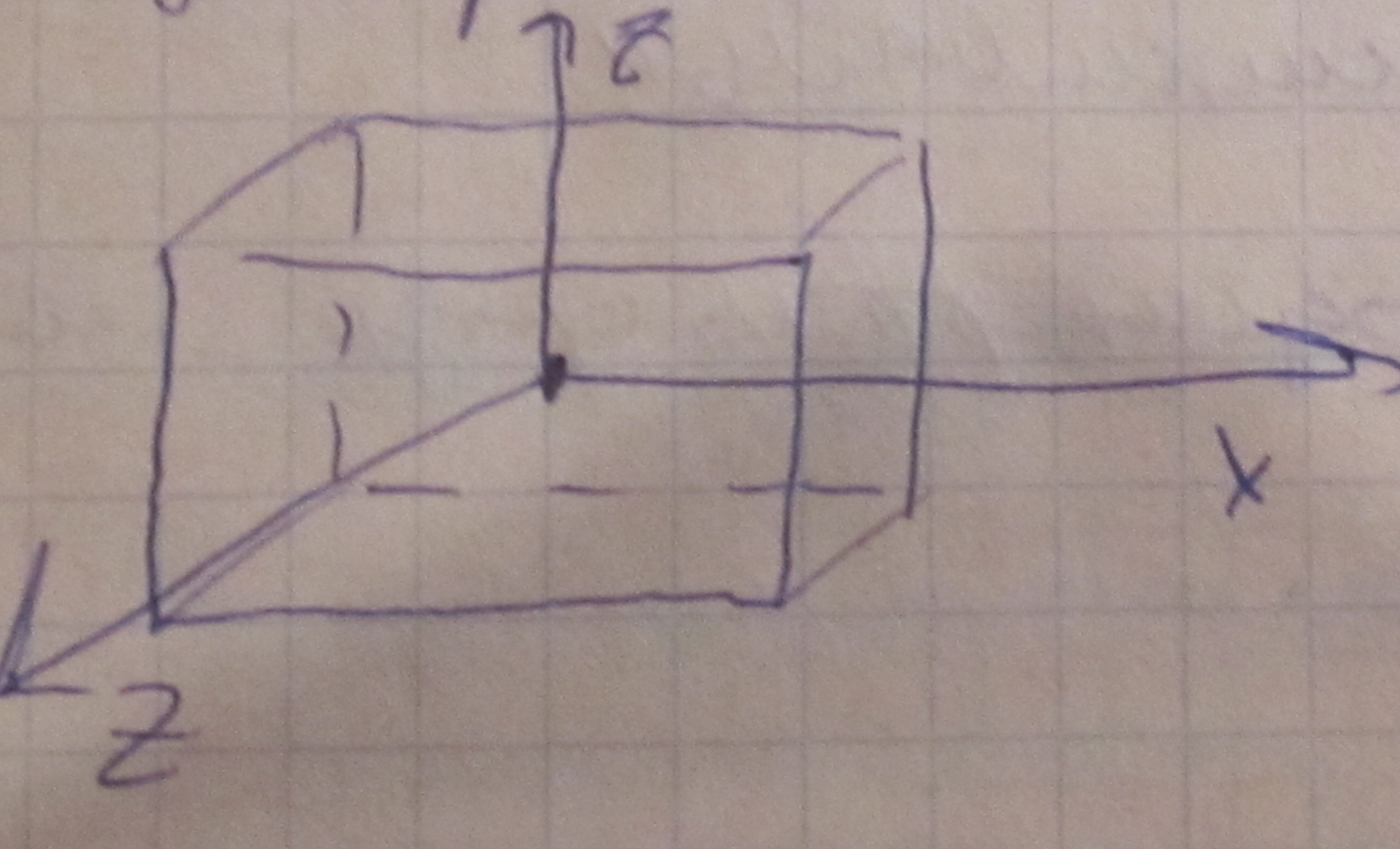
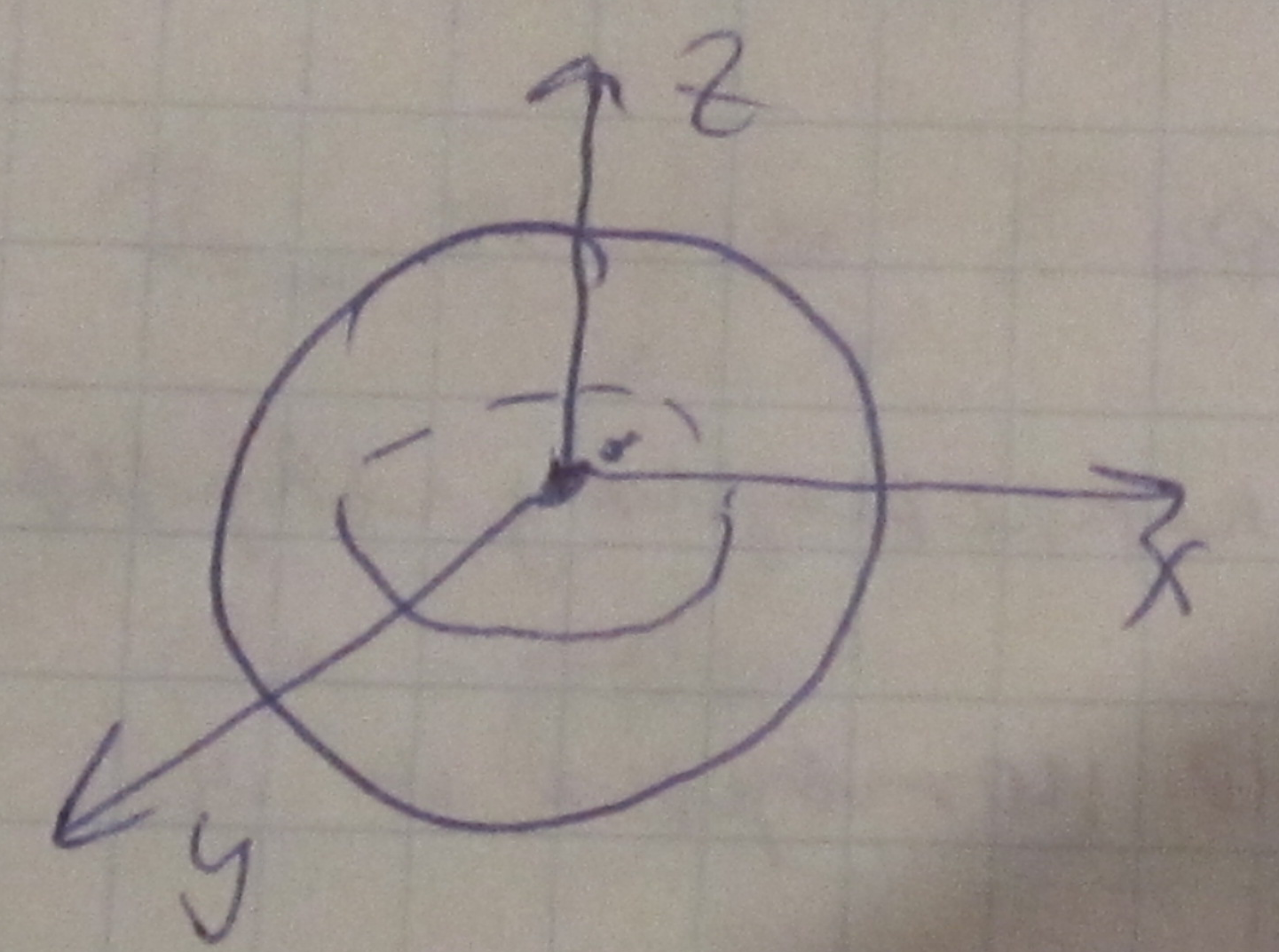
Центр главной оси инерции назыв свобод осями.

При вращение тела вокруг этих осей не возникают силы, которые могут изменить направление оси вращения, вращение тела будет устойчивым, только относительно центральной главной осей с максимальным моментом инерции и минимальным.

Вращение вокруг оси не устойчиво.

Например- У прямоугольной пирамиды Ymax и Ymin относительно осей паралельных его самой длине и самой короткой стороне.

23.Вычисление момента инерции тонкого однородного стержня относительно перпендикулярной оси.

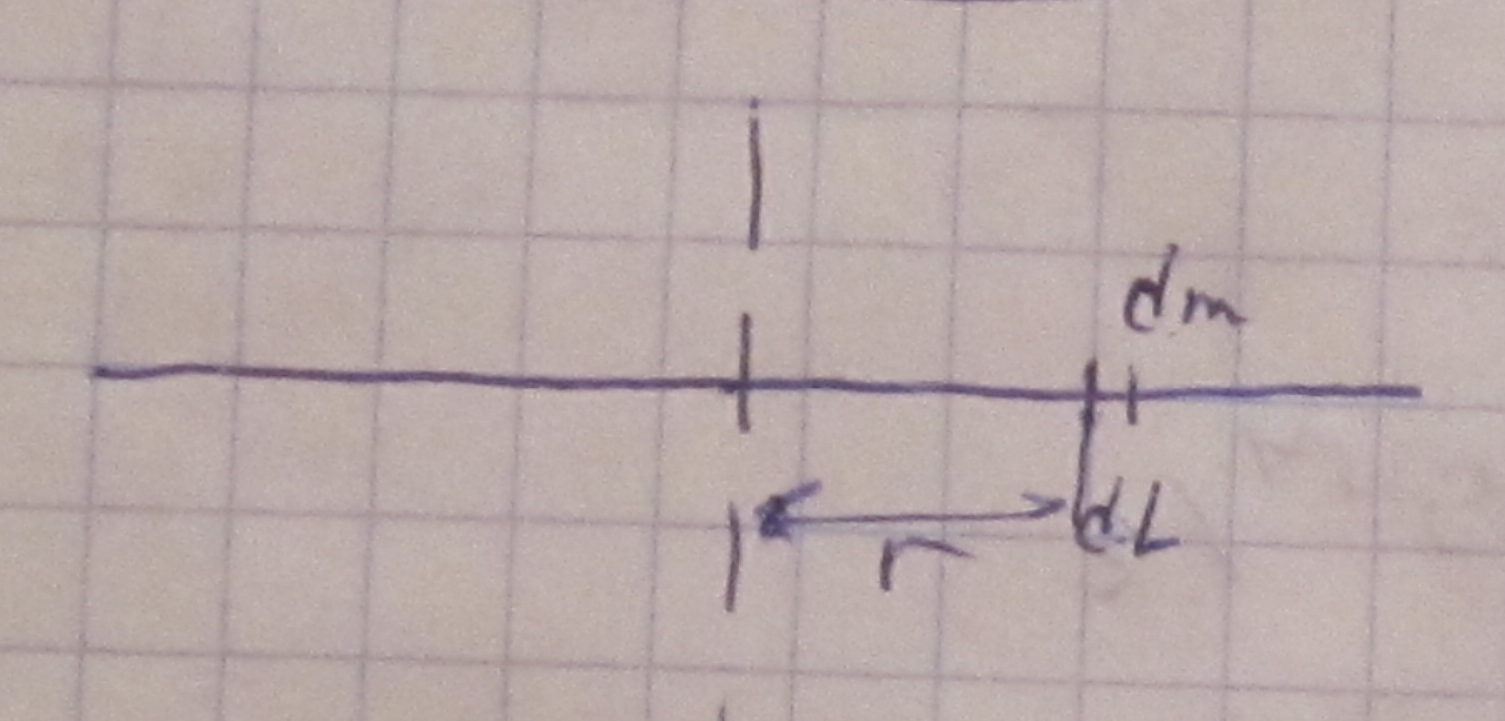
24.Вычисление момента инерции бесконечно тонкого круглого кольца относительно оси, перпендикулярной плоскости кольца.

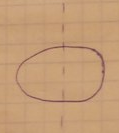
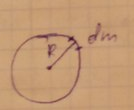
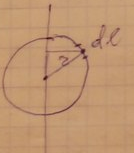
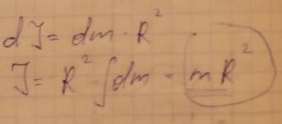
25.Вычисление момента инерции однородного сплошного диска (цилиндра) относительно продольной геометрической оси.

26.Центральный момент импульса материальной точки, системы материальных точек и тв тела.

1)момент импульса мат точки относительно неподвижной точки О.

Это вектор L

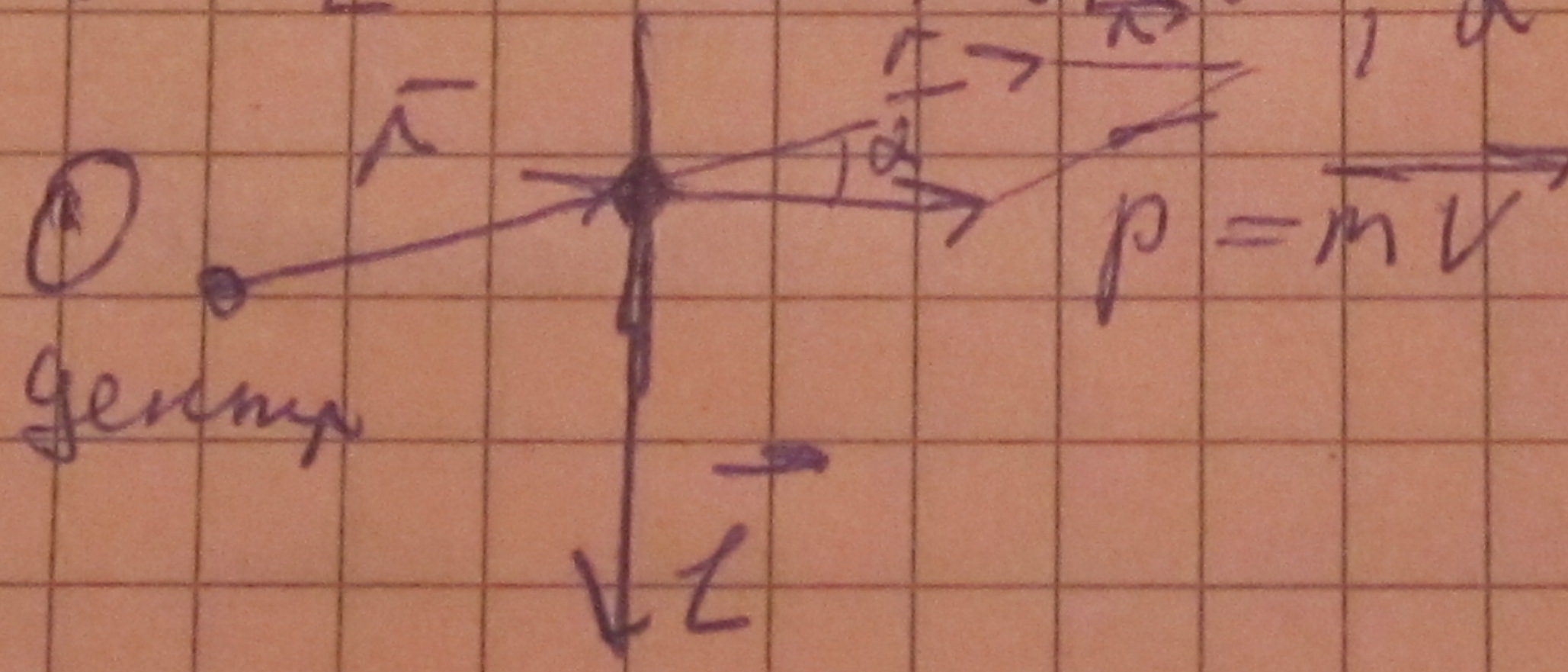
2. система м.т.

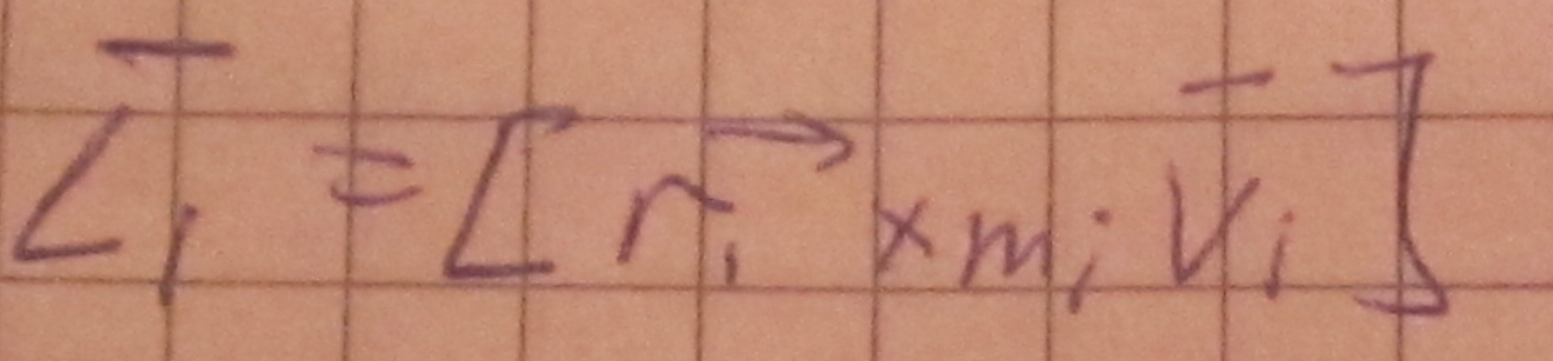
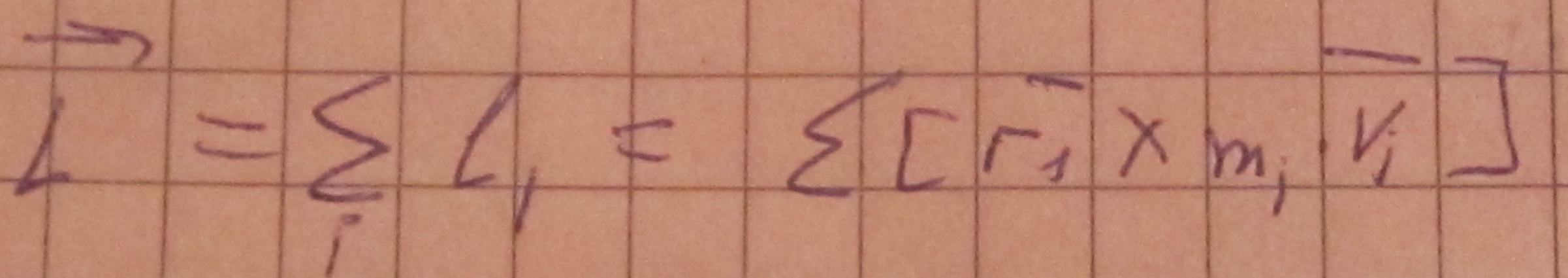
3. момент импульса тв тела (L)

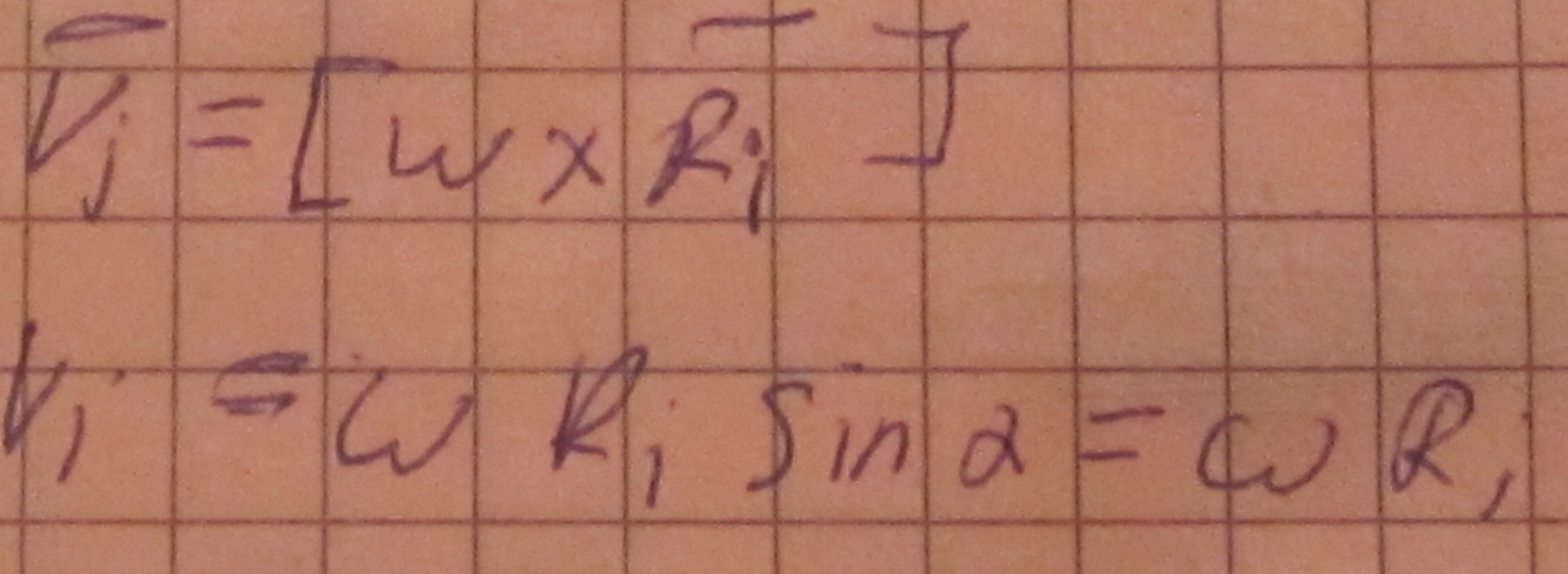, a=П/2

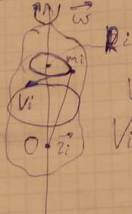
Каждая точка по радиусу ri

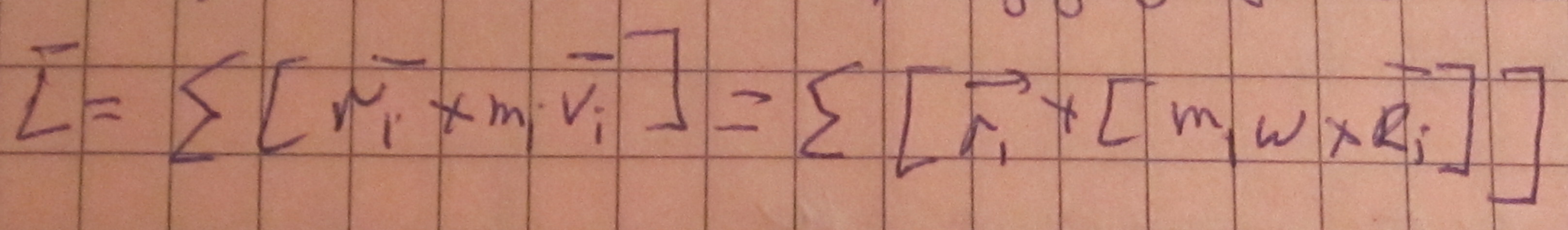
Если ось неподвижна(зафиксирована в пространстве), то Lx=wYx, Ly=wYy, Lz=wYz.