10.Вектор углового перемещения, угловая скорость, прямая и обратная связь угловой скорости и вектора углового перемещения.

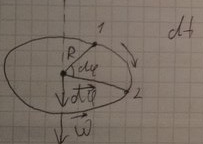
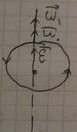
За бесконечно малый промежуток времени dt точка пермещается на бесконечно малый угол dфи.

Вектор углового пермещения характеризуется своим значение dфи и направление перпендикулярным плосокости окружности.

Направление dфи определяется правилом правого винат- если винт вращать в сторону увелечения угла dфи от 1 ко 2 то направление пост движения винта укажет направление dфи.

Свойством быть вектором обладают лишь бесконечно малые угловые премещения dфи а не конечные дельта фи.

Псевдовектор не имеет не имеет точки приложения dфи.

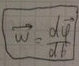
Вектор угловой скорости- вектор линейной скорости движения по окружности мат точки определяется

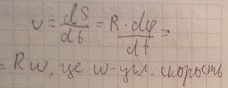
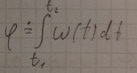
12.Связь линейных и угловых кинематических характеристик

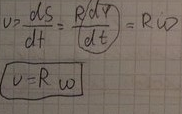
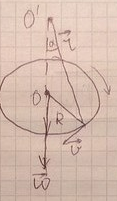
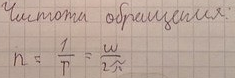
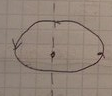
11.Угловое ускорение, прямая и обратная связь угловой скорости и углового ускорения

Кинематическая характеристика вращ движения, которая вводится при неравномерном движение.

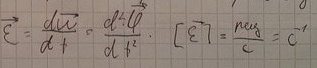
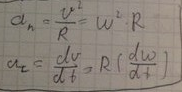
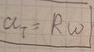
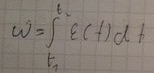
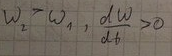
13.Инерциальные и неинерциальный со, Принцип относительно и преобразования Галилея.

Все системы отсчет эквиваленты.В динамике одно и тоже движение рассматривается по разному в разных СО.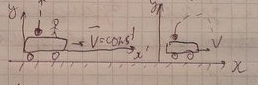

Классическая механика постулирует что все СО, в которых свобод тела движ равномерно и прямолинейно являются ИСО.

СО в которых действуют силы тяготения и в которых не выполняются 1 и 2 законы Ньютона называются НИСО.

ИСО движется без ускорения и зам вращения.

СО в которых системой является Земля не являются ИСО, так как земля вращаеттся вокруг своей оси и совершает вращение вокруг Солнца.

Центр на Солнце и оси направлены на звезды.

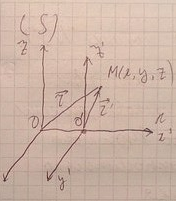
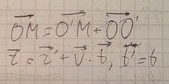
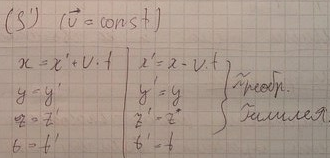
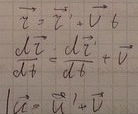
Система S является также ИСО.

Во всех ИСО механические явления , протекают одинаково, тоесть уравнения Ньютона инвариантны относительно преобразование Галилея.

14.Масса тела и его св-ва, центр масс системы.

Масса тела

основная механическая величина, определяющая величину ускорения, сообщаемого телу данной силой. М. тел прямо пропорциональны силам, сообщающим им равные ускорения и обратно пропорциональны ускорениям, сообщаемыми им равными силами. m = f/a

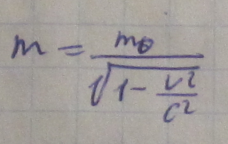
m- аддитивная величина- это масса тела, равная сумме масс, составляющих его частей.

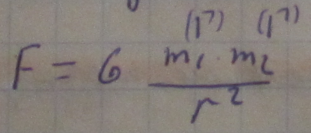
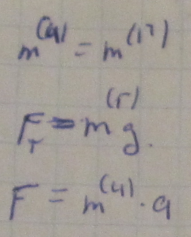
Центр масс – это точка геометрическая, радиус вектор которой равен

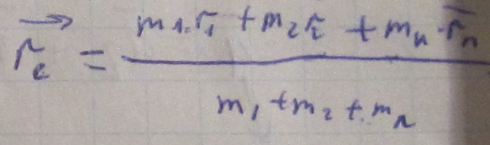
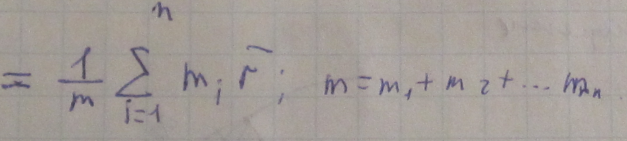
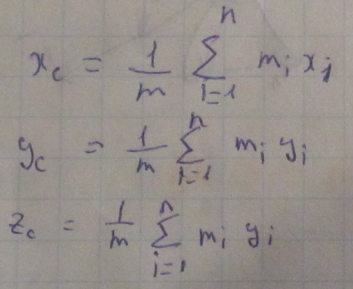
Положение точки центр масс не зависит от выбора СО, в которой оно определяется.

Утверждение справедливо в механике малых скоросетй.

Если V тела близко к C, то положение центр масс не имеет смысла.

15.Импульс материальной точки, системы Мат точки и тв тела.

1. Мат точка

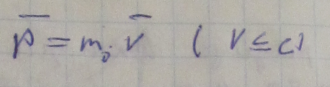
При

2. Системы Мат точки- совокупность конечного числа Мат точек.

i-я точка

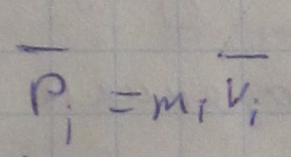
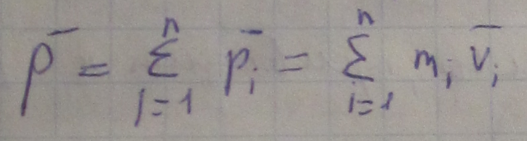
3. ТВ тело (v<<c)

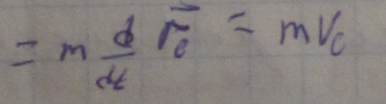
16.Фундаментальные и нефундаментальные взаимодействия, сила как мера взаимодействия, св-ва сил.

Сила – векторная колличесвенная мера интенсивности взаимодействия между телами.

F=-F. Сила – функция радиуса вектора и его скорости относ др мат точек.

F=F(r,v) векторная. Сила причина изменения скорости тела. Так как изменение V характеризуется a а=dv/dt, то динамическое проявление силы F состоит в том что тело под дейсвием этой слы движется с ускорением.

Статическое дейсвие силы приводит к тому что упругие тела под действием это сыли деформируются, газы сжимаются и тд. Если на тело дейсвует несколько сил то векторная сумма этих сил – равнодействующая сила. F1+F2+Fn

Фундаментальные и нефундаментальные взаимодействия.

Все силы, рассматриваемые в физике можно свести к 4 основным силам, кот называются фундаментальными. Данные силы обусловлены фундаментальными взаимодействиями. Фундаментальные силы — силы, кот при современном состоянии науки не могут быть сведены ни к каким другим силам.

Все фундаментальные взаимодействия: Fтр, Fупр, сила гидростатического давления, сила поверхностного натяжения, сила Архимеда

Фундаментальные взаимодействия: сильные(ядерные)-протоны, нейтроны;Э/м — все электрически заряженные частицы; слабое — элементарные частицы, гравитационное — все.