4. Описание движения в координатной и векторной форме.

Выбираем декартовую систему координат в которой положение точки характеризуесят 3 координатами.

При движение МТ каждой из этих координат изменяются со временем, т.е являются функцией времени.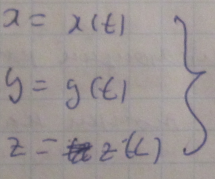 (кинематическое уравнение движенияв координатной форме)

равномерное прямолинейное движение в координатной форме.

Поскольку положение МТ на траектории определяется радиусом вектором, которое при движение этой точки зависит от t. r=r(t)

r(t)=ix(t)+jy(t)+kz(t) – кинемат уравнение движения в векторной форме

5.Киниметические параметры таректории движения

1.Путь,2.Вектор перемещения,3. Радиус вектор

1) Путь расстояние точки на траектории от начала движения (скаляр величина) S>0

2)Векто перемещения Вектор направлен от начала точки к конечнйо точки на траектории и направлен в сторону движения.

3) радиус вектор – вектор соединяющий начало отсчета с положение точки на траектории.

6.Средняя скорость перемещения и средняя путевая скорость.

Сред скорость перемещения- векторная величина, равная отношению вектора перемещения и промежутку времени, за которое это перемещение произошло

Вектор сред скорости перемещения совпадает с вектором перемещения (дельта р)

Средняя путевая V- скалярная величина, равная первой производной от пути по времени.

Если значение скорости с течение времени не изменяется, то такое движение равномерное,если же вектор скорости не изменяется, то оно равномерное и прямоллинейное.

7.Прямая и обратная связь мгновенной линейной скорости и радиуса вектора материальной точки, модуля скорости и пройденного пути.

Понятие ср.V и S приближ описание точки.

В действительности материал точка движется не по прямой а по дуге, поэтому истинное движение мат точки на траектории характеризуется мгновенной скоростью.

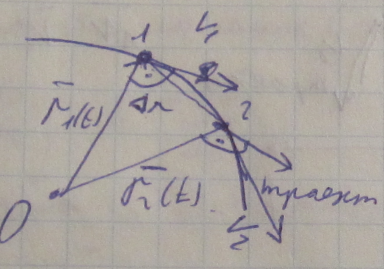
Мгновенная скорость- векторная величина, равная первой производной радиуса вектора по времени.

При дельта t стремящейся к нулю, хорда дельта r уменьшается, в пределе стремится к дельта r и следовательно вектор мгновенной скорости будет направлен по косательнйо к траектории в данной точки.

8.Линейное ускорение. Прямая и обратная связь линейного ускорения и мгновенной линейной скорости.

Лин ускорение характеризует быстроту изменения скорости.

Пусть в момент времени t1 мгновенная скорость точки была v1,а в момент t2 была v2, то среднее ускоерение материал точки за время дельта t равно

Ускорение

Обратная связь v и t.

9.Ускорение при криволинейном движение, нормальное и тангенциальное ускорение

Случай плоского движение материал точки в декартовой системе (x,y)

Тангенциальное ускорение- вектор вектор тангенциального, касательного ускорения характеризует изменение вектора скорости по величине и направлен по косательной к траектории, тоесть совпадает с вектором мгновенной скорости в данной точки.

Нормальное ускорение- вектор нормального ускорения, характеризует изменения вектора скорости по направлению.

Модуль нормального ускорения а=V^2/r квадрат модуля норм ускорения, поделеный на радиус кривизны в данной точки.

А тангенциального ускорения

Полное ускорение