43. Критерии теплового подобия.

Попытки аналитического решения конвективного теплообмена до сих пор не дали положительного результата. По этой причине большое значение имеют экспериментальные значения с последующей обработкой результатов в соответствии с теорией подобия.

Тепло от стенки через тепловой граничный слой передается путем теплопроводности, т.е. 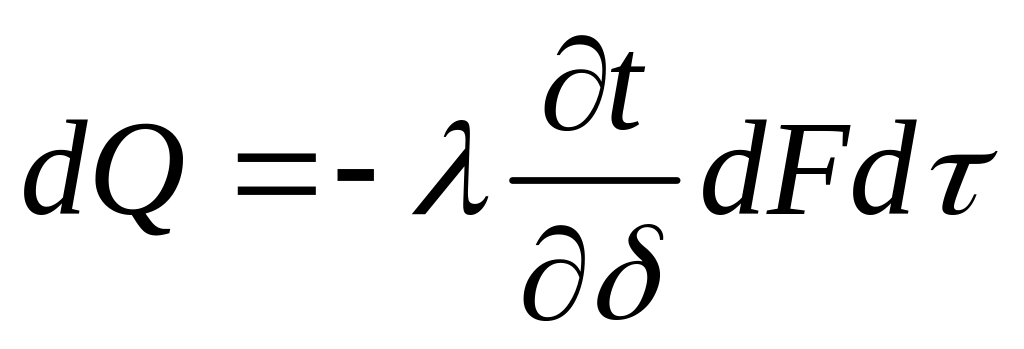, а через тело путем конвекции .

Приравняем правые части:

Разделим правую часть на левую, заменим приращение самими величинами, а величину заменим некоторым линейным размером L, тогда получим:

- критерий Нуссельта.

Равность кр. Нуссельта характеризует подобие процессов теплопереноса на границе между стенкой и потоком жидкости.

Чтобы определить другие критерии используют уравнение Фурье – Кирхгофа и произведем следующие допущения:

Примем в качестве масштаба, слагаемое, которое выражает количество тепла, которое переносится путем теплопроводности и разделим на него все остальные.

Чтобы избежать мелких чисел обычно применяют величину обратную ей:

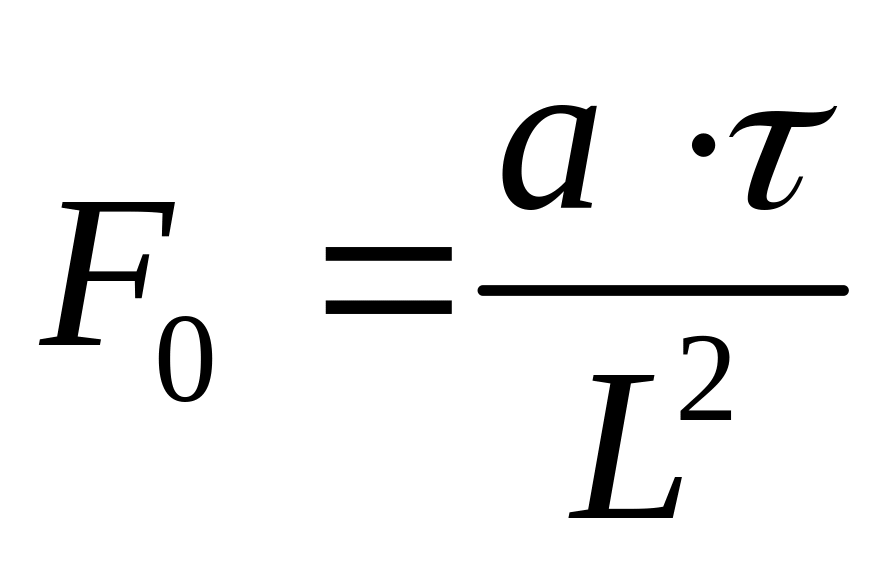- критерий Фурье

Равенство критериев Фурье в подобных точках тепловых потоков является необходимым условием подобия неустановившихся потоков – аналог гомохромности.

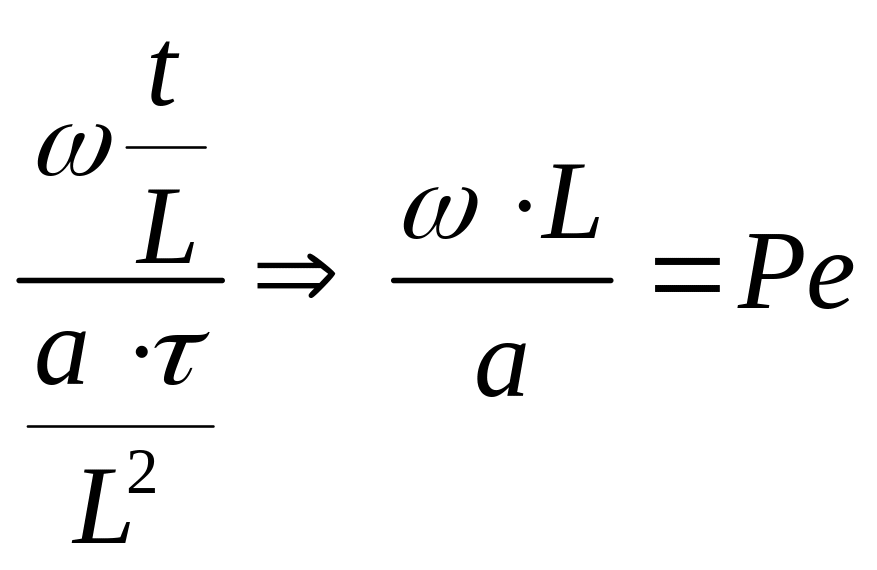- критерий Пекле

- является мерой соотношения между теплом, которое переносится конвекцией и теплопроводностью. Его можно выразить:

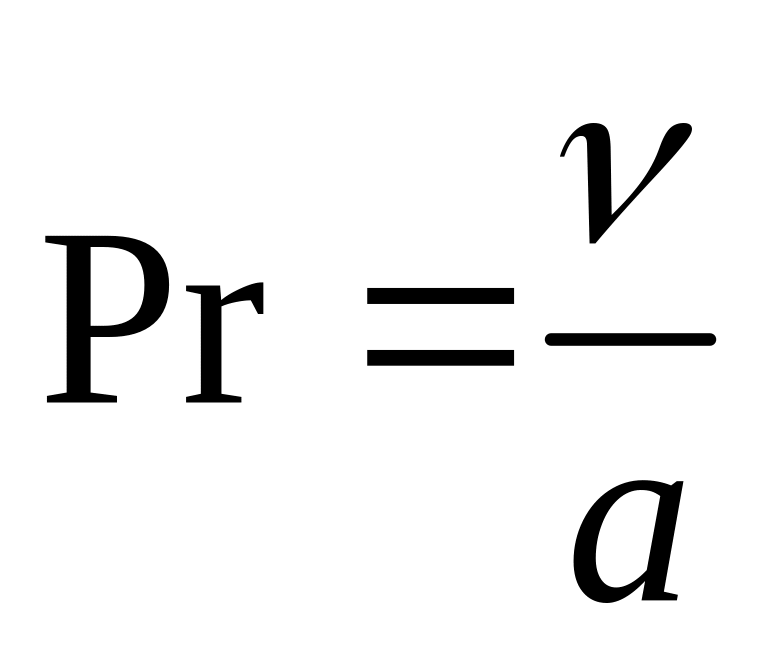- критерий Прандтля.

- состоит из физических величин, поэтому он характеризует подобие физических свойств теплоносителя пр-ов конвективного теплообмена.

Поскольку процесс теплообмена зависит от гидродинамических и геометрических параметров, то необходимыми условиями подобия тепловых процессов является равенство гидродинамических и геометрических критериев.

f(Fo, Nu, Pe, Ho, Re, Fr, L1, L2…Ln)=0 – уравнение теплового подобия.

Чаще всего определенным критерием является Nu

Nu=f(Fo, Pe, Ho, Re, Fr, L1, L2…Ln)

Поскольку искомым параметром Nu является а, то

a=f(Fo, Nu, Pe, Ho, Re, Fr, L1, L2…Ln) (*)

В зависимости от вида (режима) теплообмена в уравнении (*) пренебрегают некоторыми параметрами.