38. Закон Фурье. Перенос тепла теплопроводностью.

Закон Фурье: Процесс теплопроводности как и др. виды теплообмена может иметь место при условии, что температура в различных точках тела неодинакова, т.е. grad t≠0, тогда в соответствии с гипотезой Фурье, тепло которое проходит через элемент изотермической поверхности в единицу времени, пропорционально grad t dt/dn:

dQ= - ·dF·dτ·λ (*)

где λ – коэффициент пропорциональности или коэффициент теплопроводности, который представляет собой физический параметр вещества (с размерностью Вт/(м·К)).

Физический смысл: λ показывает какое количество тепла проходит за счет теплопроводности в единицу времени через единицу поверхности при grad t=1.

Для расчета количества тепла, которое проходит за время δt, через всю поверхность F, уравнение (*) необходимо проинтегрировать.

Коэффициент λ зависит:

- природы вещества;

- структуры вещества;

- температуры.

Для газов: λ с увеличением температуры растет; для идеальных газов она не зависит от давления, а для водяного пара – зависит.

Для жидкости: λ при повышении температуры снижается (за исключением глицериновой воды, при повышении давления – λ растет).

Для металлов: очень важно чистые они или с примесями. Например, чистая медь имеет , а с примесью 0,01% As (мышьяк) – 142 Вт/(м·К). Для твердых материалов, неметаллов λ зависит от пористости и влажности.

39. Дифференциальное уравнение Фурье.

При решении различных задач, которые связаны с теплообменным путем теплопроводности необходимо иметь систему дифференциальных уравнений, которые описывали бы распространение температур в пространстве и во времени.

Поскольку величины, влияющие на теплопроводность, также меняются и в пространстве и во времени, то при выводе диф. уравнения сделаем следующие допущения:

1. тело однородно и изотропно;

2. физические параметры постоянны во времени;

3. деформация объема отсутствует;

4. внутренние источники тепла распределены равномерно.

Количество тепла, которое подводится к граням параллелепипеда Qx, Qy, Qz, а количество тепла, которое отводится через противоположные грани в тех же направлениях, обозначим Qx+dx, Qy+dy, Qz+dz.

Будем считать, что температура на гранях = t, а температура граней, с которых отводится t+ ; t+ ; t+ .

Тогда, используя уравнение Фурье: количество тепла, которое подводится к граням dτ, может быть записано:

Количество тепла, которое отводится через противоположные грани за то же время может быть записано в виде:

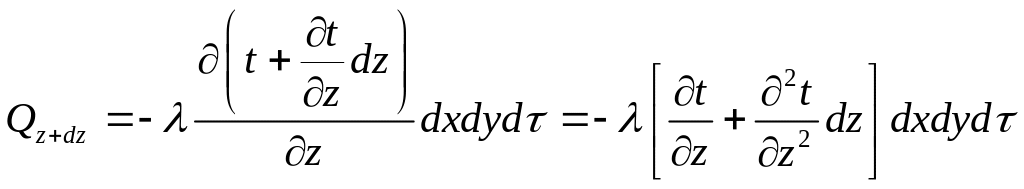
Поскольку часть тепла расходуется на повышение температуры в элементарном объёме, то количество тепла которое подводится, будет отличаться от количества тепла которое отводится. Разность тепла между гранями можно записать:

Тогда приращение тепла по всему V:

- изменение тепла в элементарном объёме.

- оператор Лапласа

Если в dV существуют источники тепла, то его необходимо учитывать. Обозначим количество тепла, которое выделяется внутренними источниками в единице объёма dV за время , через величину , тогда

Учитывая величину получим полное приращение тепла:

По закону сохранения энергии при изобарном процессе (p=const) приращение количества тепла расходуется на изменение энтальпии:

где в свою очередь:

При изохорном процессе (V=const) приращение тепла идет на изменение внутренней энергии:

где в свою очередь:

Для твердых тел можно принять, что:

, тогда:

(*)

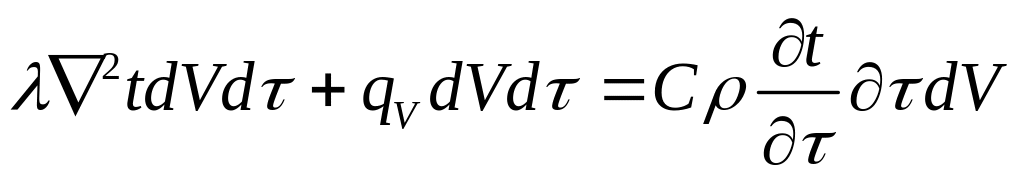
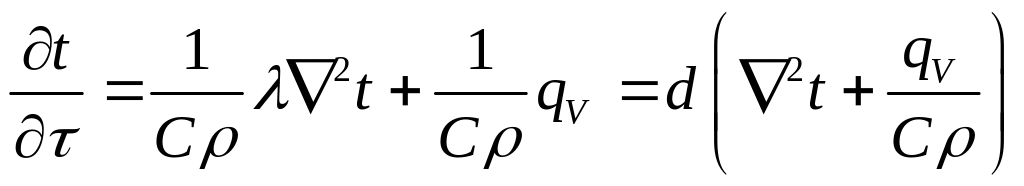где - коэффициент теплопроводности

- физическая величина, которая характеризует скорость изменения температуры. Чем больше , тем больше скорость изменения температуры любой точки тела

Уравнение (*) называется ДУ теплопроводности неподвижной среды. Допустим, что = 0, тогда - получ. уравнение Фурье.

Если присутствует, а температура не меняется во времени, то уравнение превращается в уравнение Пуассона:

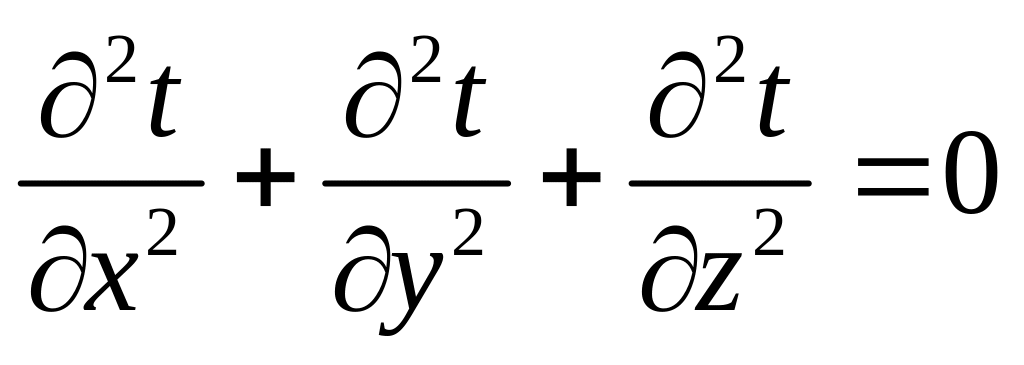; : - уравнение Лапласа.

Уравнение Фурье, Пуассона и Лапласа описывает изменение температуры при передачи тепла теплопроводностью в самом общем виде. Для конкретных расчетов они должны быть дополнены условиями однозначности (размеры и формы тела, физические свойства тела и начальные либо граничные условия).