1.6. Метод ветвей и границ

В ряде задач оптимизации удается добиться более существенного сокращения перебора, используя подход, известный как метод ветвей и границ. Заметим сразу, что этот метод не выходит за рамки хорошо организованного исчерпывающего перебора, а потому, с одной стороны, наверняка находит оптимальный план, но с другой, не позволяет надеяться на волшебное ускорение работы. Тем не менее этот метод позволил решать ряд практических задач оптимизации, которые ранее считались безнадежно трудоемкими.

Метод ветвей и границ представляет собой не конкретный алгоритм, а скорее подход к рассмотрению задачи, с помощью которого (но и при учете специфики конкретной задачи) иногда удается построить эффективные алгоритмы. Рассмотрим, в чем заключается этот подход.

Пусть U - множество всех допустимых планов задачи оптимизации и F(X) - целевая функция, подлежащая минимизации. Разделим каким-то образом множество U на два непересекающихся подмножества U⁰ и U¹. При этом постараемся провести разделение так, чтобы множество U⁰ было «поменьше и получше», т.е. с наибольшей вероятностью содержало искомый оптимальный план и при этом было невелико по мощности. Практически разделение можно выполнить, например, так: выбрать какое-то «наиболее перспективное» значение одной из переменных и отнести к U⁰ все планы с этим значением переменной. Далее аналогичным образом разделим U⁰ на два множества U⁰⁰ и U⁰¹, затем разделим U⁰⁰ на U⁰⁰⁰ и U⁰⁰¹ и т.д. На некотором шаге придем к множеству, содержащему только один план. Чтобы не плодить индексы, предположим, что это произошло на четвертом шаге: U⁰⁰⁰⁰ = {X₀}. Результат разделения множеств показан на рис.1.2. Получен некоторый допустимый план X₀. Не является ли он оптимальным?

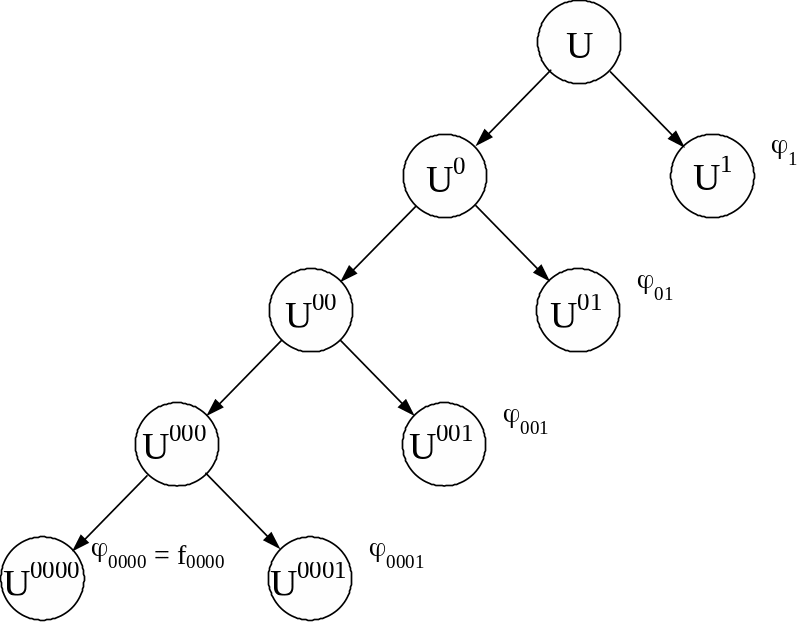
Рис.1.2

Пусть имеется какая-то достаточно просто вычисляемая функция (W), дающая оценку снизу для любого подмножества W Í U, т.е. (W) £ F(X) для любого X Î W.¹ Оценка не обязательно должна быть точной, т.е. на самом деле, возможно, минимум F(X) при X Î W больше, чем оценка (W). Однако чем она точнее, тем лучше будет работать алгоритм.

Вычислим значение целевой функции F(X₀) и сравним его с оценкой (U⁰⁰⁰¹). Если F(X₀) £ (U⁰⁰⁰¹), то план X₀ является лучшим среди всего подмножества U⁰⁰⁰. Мы выяснили это, не выполняя перебора планов из U⁰⁰⁰¹. В этом случае следует подняться по дереву и вычислить оценку U⁰⁰¹. Если, на наше счастье, F(X₀) £ (U⁰⁰¹), то план X₀ является лучшим на подмножестве U⁰⁰ и т.д.

Что, если на каком-то шаге подъема по дереву оценка (W) не позволит отсечь очередное подмножество без рассмотрения? Пусть, например, F(X₀) > (U⁰¹). Тогда следует разделить U⁰¹ на U⁰¹⁰ и U⁰¹¹, U⁰¹⁰ на U⁰¹⁰⁰ и U⁰¹¹¹ и т.д., то есть выполнить спуск еще по одной ветви дерева. При этом будет получен другой план, назовем его X₁. После этого следует запомнить лучший из двух планов в качестве рекорда и в дальнейшем использовать его для сравнения с нижними оценками множеств.

Работа алгоритма будет завершена тогда, когда каждое из построенных подмножеств будет либо состоять из одного элемента, для которого можно вычислить целевую функцию, либо будет исключено из рассмотрения на основании сравнения нижней оценки целевой функции на множестве с текущим рекордом.

Итак, применение метода ветвей и границ к задаче комбинаторной оптимизации предполагает выполнение следующих операций:

• Последовательное разделение множества планов задачи на непересекающиеся подмножества.

• Подсчет оценок снизу для всех подмножеств планов.

• После того, как в результате разделения получен хотя бы один допустимый план задачи, сравнение целевой функции для рекордного плана с нижними оценками подмножеств и отбрасывание тех подмножеств, которые заведомо не могут улучшить рекорд.

В самом худшем случае, если нижняя оценка не позволит исключить ни одно подмножество, алгоритм сведется к полному перебору всех планов задачи. Однако если при разработке алгоритма удалось придумать удачный способ разбиения множества и построить достаточно хорошую нижнюю оценку, то число рассмотренных планов может быть значительно уменьшено. Трудно оценить это уменьшение количественно, однако на основании опыта применения метода ветвей и границ принято считать, что число рассмотренных планов обычно примерно равно квадратному корню из их общего количества. Учитывая экспоненциальный характер роста числа планов в зависимости от размерности задачи, можно сделать вывод, что метод ветвей и границ при его успешном применении позволяет примерно вдвое увеличить размерность задач, которые могут быть решены за то же время.

Не существует общих правил для разбиения множеств и построения оценок. Алгоритмы для конкретных задач должны строиться индивидуально, на основании учета особенностей задачи.

Рассмотрим пример применения метода ветвей и границ для решения задачи о коммивояжере. Соответствующий алгоритм разработан группой авторов и называется алгоритмом Литл, Мерти, Суини и Карел. Шаги алгоритма будут показаны на конкретном числовом примере.

Пусть дана задача о коммивояжере с 5 городами и несимметричной матрицей расстояний A, показанной в табл.1.1. Для такой малой размерности задачу проще всего было бы решить полным перебором маршрутов, однако при большей размерности алгоритм ветвей и границ работает значительно быстрее.

Таблица 1.1

A	1	2	3	4	5	i
1		25	40	31	27	25
2	5		17	30	25	5
3	19	15		6	1	1
4	9	50	24		6	6
5	22	8	7	10		7
j	0	0	0	3	0	 = 47

На каждом шаге алгоритма предварительно выполняется операция приведения матрицы, которая заключается в следующем. Пусть _i – минимальное расстояние в i-той строке матрицы. Выпишем значение _i в дополнительном столбце справа и вычтем его из всех элементов строки. Затем выполним такую же операцию со столбцами матрицы. Подсчитаем сумму всех _i. В данном примере суммарное значение  = 47. Получившаяся после приведения матрица A показана в табл.1.2.

Таблица 1.2

A	1	2	3	4	5
1		0	15	3	2
2	0 (15)		12	22	20
3	18	14		2	0 (2)
4	3	44	18		0 (3)
5	15	1	0 (12)	0 (2)	

В чем смысл выполненной операции? Вычитая одно и то же число из всех элементов строки (т.е. из всех расстояний от данного города до других городов), мы уменьшаем на это число длину всех возможных маршрутов коммивояжера, поскольку каждый допустимый маршрут ровно один раз проходит через каждый город. Величина  показывает, на сколько длина приведенного маршрута меньше длины исходного. Ясно, что после приведения кратчайший маршрут останется кратчайшим. Зато теперь можно легко получить оценку снизу для всего множества маршрутов исходной задачи. Поскольку для приведенной матрицы кратчайший маршрут не может иметь длину меньше 0, то для исходной матрицы кратчайший маршрут имеет длину не менее .

Теперь следует продумать способ разделения множества маршрутов. Выберем один из элементов матрицы a_ij, определяющий расстояние от города i до города j, и разделим все множество маршрутов на две неравные части: те маршруты, которые включают путь из i в j (U₀), и те, которые не включают этот путь (U₁). Чтобы меньшее множество U₀ было более перспективным, надо выбрать такой элемент a_ij, который с наибольшей вероятностью входит в оптимальный маршрут. В качестве такого элемента разумно выбрать один из нулевых элементов матрицы A, однако какой именно? Вероятно, тот, отказ от которого приведет к наибольшим потерям. Как можно подсчитать потери, связанные с отказом от использования пути из города i в город j? Во-первых, из города i все равно придется куда-то ехать, поэтому в суммарную длину маршрута вместо слагаемого a_ij = 0 войдет некоторый элемент i-той строки a_ik, где k  j. Минимальное по i-той строке значение a_ik дает оценку связанных с этим потерь. Во-вторых, в город j надо будет откуда-то приехать, и минимальное по столбцу значение a_rj, где r  i, даст оценку потерь от того, что коммивояжер приехал не из города i. Общая оценка потерь _ij равна сумме оценок по строке и по столбцу.

В табл.1.2 возле каждого нулевого элемента матрицы в скобках показаны величины _ij – оценки потерь в случае неиспользования данного пути в маршруте коммивояжера. Как видно из таблицы, наибольшее значение оценки ₂₁ = 15. Исходя из этого, выберем в качестве U₀ множество всех маршрутов, в которых используется путь из города 2 в город 1, тогда U₁ будет содержать все остальные маршруты. Нижняя оценка целевой функции для множества U₁ будет равна ₁ =  + ₂₁ = 62.

Чтобы продолжить построение наиболее перспективного плана, рассмотрим множество U₀. Для определения остальных путей маршрута построим матрицу A₀ путем вычеркивания из матрицы A строки 2 и столбца 1, поскольку они уже использованы. Кроме того, так как использован путь 2  1, то нельзя использовать путь 1  2, поэтому положим a₁₂ = . Получившаяся матрица показана в табл.1.3.

Таблица 1.3

A0	2	3	4	5	i
1		15	3	2	2
3	14		2	0	0
4	44	18		0	0
5	1	0	0		0
j	1	0	3	0	 = 3

Выполним описанную выше операцию приведения и получим матрицу A₀ (табл.1.4). Поскольку величина приведения  = 3, можно сделать вывод, что нижняя оценка множества U₀ будет равна ₀ = 47 + 3 = 50.

Таблица 1.4

A0	2	3	4	5
1		13	1	0 (1)
3	13		2	0 (2)
4	43	18		0 (18)
5	0 (13)	0 (13)	0 (1)	

Как и на предыдущем шаге, получим оценки потерь для всех нулевых элементов матрицы _ij. Максимальное значение имеет ₄₅ = 18. Выберем в качестве U₀₀ множество маршрутов из U₀, включающих путь 4  5, тогда U₀₁ – маршруты, которые включают путь 2  1, но не включают 4  5. Имеем нижнюю оценку ₀₁ = ₀ + ₄₅ = 50 + 18 = 68.

Для множества U₀₀ построим матрицу A₀₀, вычеркнув из A₀ строку 4 и столбец 5 и положив a₅₄ = . Матрица показана в табл.1.5.

Таблица 1.5

A00	2	3	4	i
1		13	1	1
3	13		2	2
5	0	0		0
j	0	0	0	 = 3

В табл.1.6 показана приведенная матрица A₀₀. Нижняя оценка множества U₀₀ будет равна ₀₀ = 50 + 3 = 53.

Таблица 1.6

A00	2	3	4
1		12	0 (12)
3	11		0 (11)
5	0 (11)	0 (12)	0 (0)

Два нулевых элемента имеют одинаковые оценки потерь: ₁₄ = ₅₃ = 12. Возьмем любой из них¹, например, a₁₄. Для множества U₀₀₁ (всех маршрутов из U₀₀, не включающих путь 1  4), получаем нижнюю оценку ₀₀₁ = ₀₀ + ₁₄ = 53 + 12 = 65.

Чтобы ускорить дело, обратим внимание, что мы уже включили в строящийся маршрут пути 2  1, 4  5 и 1  4, что составляет цепочку 2  1  4  5. Ее можно единственным образом достроить до замкнутого маршрута, включив город 3 (другими словами, множество U₀₀₀ состоит из единственного элемента). Тогда, если для порядка начать с города 1, получается маршрут: 1  4  5  3  2  1. Длину этого маршрута можно подсчитать разными способами, например, добавив к оценке ₀₀ = 53 длины путей a₅₃ = 0 и a₃₂ = 11, а можно и просто суммировать длины всех пяти путей из исходной матрицы. В любом случае получается число f₀₀₀ = 64, которое будет первым рекордом при решении данной задачи.

Является ли данный рекордный маршрут оптимальным? Попробуем для ответа на этот вопрос использовать имеющиеся нижние оценки множеств. Оценка ₀₀₁ = 65, и это значит, что в множестве U₀₀₁ все маршруты, по крайней мере, на 1 длиннее, чем полученный рекорд, поэтому множество U₀₀₁ можно не рассматривать. Тем более бесперспективно множество U₀₁, для которого ₀₁ = 68. Однако для множества U₁ нижняя оценка ₁ = 62, а это значит, что множество вполне может содержать маршрут с длиной, меньшей чем 64. Придется для U₁ вновь выполнять процедуру разделения, строить нижние оценки и искать новый рекордный маршрут.

Вспомним, что множество U₁ состоит из всех маршрутов, не использующих путь 2  1. Чтобы отразить это условие, достаточно в приведенной матрице A положить элемент a₂₁ = . Полученная матрица A₁ показана в табл.1.7.

Таблица 1.7

A1	1	2	3	4	5	i
1		0	15	3	2	0
2			12	22	20	12
3	18	14		2	0	0
4	3	44	18		0	0
5	15	1	0	0		0
j	3	0	0	0	0	 = 15

После приведения получится матрица A₁ (табл.1.8). Нижняя оценка для U₁, как уже говорилось выше, ₁ = 62.

Таблица 1.8

A1	1	2	3	4	5
1		0 (3)	15	3	2
2			0 (8)	10	8
3	15	14		2	0 (2)
4	0 (12)	44	18		0 (0)
5	12	1	0 (0)	0 (2)	

Выбираем нулевой элемент с максимальной оценкой ₄₁ = 12. Получим два множества: U₁₀ – маршруты, которые не включают путь 2  1, но включают 4  1, и U₁₁ – маршруты, которые не включают ни путь 2  1, ни путь 4  1. Нижняя оценка ₁₁ = ₁ + ₄₁ = 62 + 12 = 74, т.е. множество U₁₁ можно отбросить сразу – оно содержит маршруты, заведомо худшие, чем текущий рекорд.

Матрица A₁₀ для множества U₁₀ показана в табл.1.9.

Таблица 1.9

A10	2	3	4	5	i
1	0 (3)	15		2	0
2		0 (8)	10	8	0
3	14		2	0 (4)	0
5	1	0 (0)	0 (2)		0
j	0	0	0	0	 = 0

Приведение ничего не дает, поэтому нижняя оценка ₁₀ = ₁ = 62 и сразу можно вычислять оценки нулевых элементов. Выбираем ₂₃ = 8. Для множества U₁₀₁ оценка ₁₀₁ = ₁₀ + ₂₃ = 62 + 8 = 70, значит, множество U₁₀₁ также можно не рассматривать. Множество U₁₀₀ содержит маршруты, которые не включают путь 2  1, но включают 4  1 и 2  3. Матрица A₁₀₀ показана в табл.1.10.

Таблица 1.10

A100	2	4	5	i
1	0 (3)		2	0
3		2	0 (4)	0
5	1	0 (3)		0
j	0	0	0	 = 0

Приведение ничего не дает, нижняя оценка ₁₀₀ = ₁₀ = 62. Вычисляем оценки нулевых элементов и выбираем ₃₅ = 8. Для множества U₁₀₀₁ оценка ₁₀₀₁ = ₁₀₀ + ₃₅ = 62 + 4 = 66, поэтому U₁₀₀₁ не рассматриваем. Множество U₁₀₀₀ содержит маршруты, которые включают 4  1, 2  3 и 3  5. Единственный маршрут, который можно достроить (множество U₁₀₀₀), выглядит так: 1  2  3  5  4  1. Длина этого маршрута f₁₀₀₀ = 62, что лучше, чем прежний рекорд!

Поскольку все нерассмотренные множества были забракованы с помощью сравнения их нижних оценок с рекордом, перебор можно считать законченным, и текущий рекордный маршрут является кратчайшим маршрутом коммивояжера для данной задачи. Интересно отметить, что при решении задачи были полностью построены только два маршрута (всего для задачи с пятью городами возможны 24 разных маршрута).

На рис.1.3 показан просмотренный фрагмент дерева перебора. Рисунок позволяет более наглядно убедиться, что проведенный поиск действительно был исчерпывающим. Жирными стрелками выделены те ветви дерева перебора, которые были рассмотрены до конца.

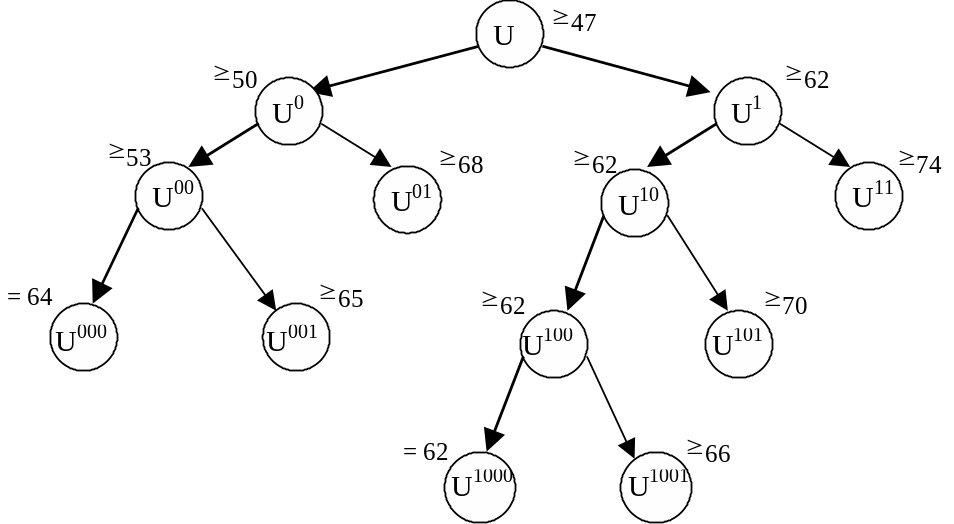
Рис.1.3