66 Течение неньютоновских жидкостей. Их классификация.

Жидкости, которые подчиняются закону внутреннего трения Ньютона:

,

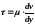где  – напряжение сдвига; μ – динамический коэффициент вязкости (динамическая вязкость); dv/dy – градиент скорости, называются ньютоновскими.

В технологии строительных материалов к таким жидкостям относятся цементные шламы и растворы, бетонная смесь, глиняные шликеры и пасты, растворы полимеров, краски и т.п. Графики, выражающие зависимость изменения предельного напряжения сдвига τ от градиента скорости dv/dy, носят название кривых течения. В современной теории неньютоновские жидкости подразделяют на три класса

К первому классу относятся вязкие или стационарные неньютоновские жидкости.

Ко второму классу относятся неньютоновские жидкости, характеристики которых зависят от времени (нестационарные жидкости). Для этих структур кажущаяся вязкость определяется не только градиентом скорости сдвига, но и его продолжительностью.

К третьему классу относятся вязкоупругие или максвелловские жидкости. Жидкости текут под действием напряжений сдвига, но после снятия напряжений частично восстанавливают свою форму.

67 Характеристики бингамовских, псевдопластичных и дилатантных жидкостей.

Течение бингамовских жидкостей начинается только после того, как касательные напряжения в них достигнут некоторого предельного значения (так называемого начального напряжения сдвига ₀). При меньших касательных напряжениях (<₀) эти жидкости не текут, а испытывают только упругие деформации, как твердые тела (рис. 4.9, кривые течения 2 и 3).

Считается, что структура тела Бингама под действием предельного напряжения сдвига мгновенно и полностью разрушается, в результате чего тело Бингама превращается в жидкость. При снятии напряжения структура восстанавливается, и тело возвращается к твердому состоянию.

В бингамовских жидкостях касательное напряжение определяется по формуле Шведова-Бингама:

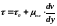, (4.33)

где ₀ – начальное (предельное) напряжение сдвига (для ньютоновских жидкостей ₀ = 0); μ_пл – пластическая вязкость постоянна и аналогична вязкости ньютоновской жидкости

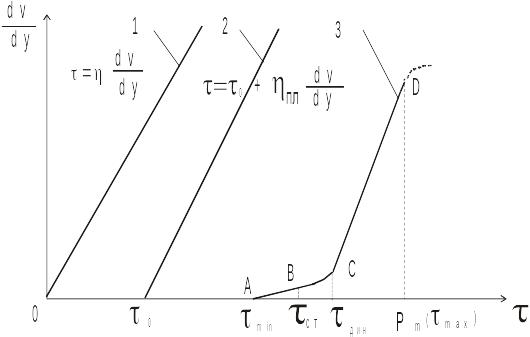
1 – ньютоновская жидкость; 2 – бингамовская неструктурированная жидкость;

3 – бингамовская структурированная жидкость

Псевдопластичные жидкости (рис. 4.10), как и ньютоновские, начинают течь уже при самых малых значениях τ, т.е. у них нет предела текучести.

Значение вязкости таких жидкостей в каждой конкретной точке зависит от градиента скорости. Поэтому течение таких жидкостей характеризуют кажущейся вязкостью, которая представляет собой отношение напряжений сдвига к градиенту скорости. С увеличением скорости сдвига кажущаяся вязкость этих жидкостей уменьшается.

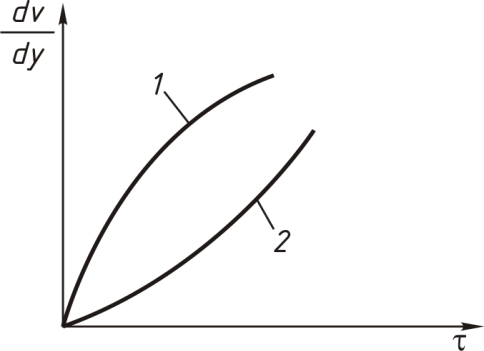
Рисунок 4.10 – Кривые течения псевдопластичных (1) и дилатантных (2) жидкостей

К дилатантным жидкостям относятся суспензии крахмала, различные клеи с большим содержанием твердой фазы. В отличие от псевдопластичных, эти жидкости характеризуются возрастанием кажущейся вязкости с увеличением градиента скорости. Течение их может быть описано также уравнением Оствальда при m > 1.

Рисунок 4.10 – Кривые течения псевдопластичных (1) и дилатантных (2) жидкостей