53 Ламинарный режим обтекания твердого тела жидкостью. Решение (закон)Стокса для силы давления потока.

При небольших скоростях и малых размерах тел или при высокой вязкости среды режим движения ламинарный, тело окружено пограничным слоем жидкости и плавно обтекается потоком (рис. 4.2).

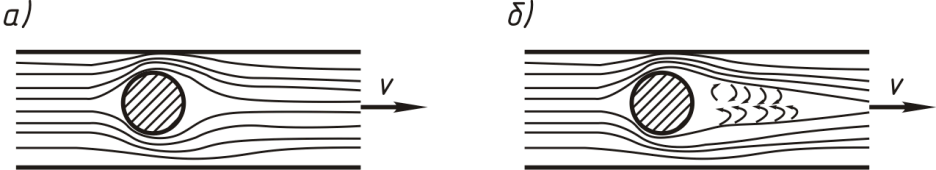
(а) – ламинарный режим; (б) – турбулентный режим

Рисунок 4.2 – Обтекание жидкостью твердого тела

Потеря давления в этом случае связана главным образом с преодолением сопротивления трения. При обтекании тела в форме шара потоком вязкой жидкости, когда основным фактором, определяющим сопротивление, являются силы трения, силу сопротивления определяют по формуле Стокса

,

где d – диаметр шара; μ – динамическая вязкость жидкости; – скорость потока жидкости.

54 Турбулентный режим обтекания твердого тела жидкостью. Формула Ньютона для определения полного сопротивления.

C развитием турбулентного движения в потоке возникают различные завихрения и образование воздушных пузырьков.

В общем случае сопротивление при обтекании потока жидкости или тела в покоящейся жидкости, представляет собой сумму сопротивлений трения и давления (сопротивления формы). Суммарное(полное) сопротивление (часть его называется лобовым) обычно определяется по формуле Ньютона:

(1)

где с – коэффициент лобового сопротивления;

S – площадь сечения обтекаемого тела по Миделю (площадь проекции тела на плоскость перпендикулярная векторам скорости набегающего потока);

- плотность жидкости; V – скорость потока жидкости.

Коэффициент лобового сопротивления «с» зависит от формы обтекаемого тела и числа Рейнольдса Re. При исследовании движения шарообразных частиц диаметром d были установлены 3-и области, каждой из которых соответствуют определенные характерные зависимости «с» от «Re» (с=f(Re)):

Ламинарная область (область действия законов Стокса):

Переходная область:

Автомодельная область:

Подставляя в уравнение (1) значение «с», видим, что в ламинарной области сила сопротивления пропорциональна скорости (F~V):

В переходной области F~V^1.4, в автомодельной области F~V², поэтому ее называют областью квадратичного сопротивления.

При обтекании форм значительно отличающихся от формы шара, значения коэффициентов значительно больше и зависят не только от критериев Рейнольдса, но и от факторов формы: , где - поверхность шара имеющая тот же объем, что и рассматриваемая поверхность .

55 Осаждение частиц под действием силы тяжести. Скорость витания частицы.

В инженерной практике часто приходится иметь дело с движением 2-ухфазной жидкостью (жидкость + смесь твердых частиц). Законы движения таких жидкостей имеют поэтому большое значение. В промышленности СМ взвесенесущие потоки применяют при пневмотранспорте цемента, гидро транспорте бетонной смеси, сушке и обжиге сыпучих материалов во взвешенном состоянии и других технологических процессах.

Особенности взвесенесущих потоков в значительной степени определяются характером обтекания твердых частиц потоком жидкости или газа.

Пусть в вертикальной трубе диаметром D движется частица в форме шара диаметром d, причем D>>d. Поток вязкой жидкости направлен снизу вверх, скорость потока V. На частицу действует сила F (давление потока) и сила тежести G=mg.

С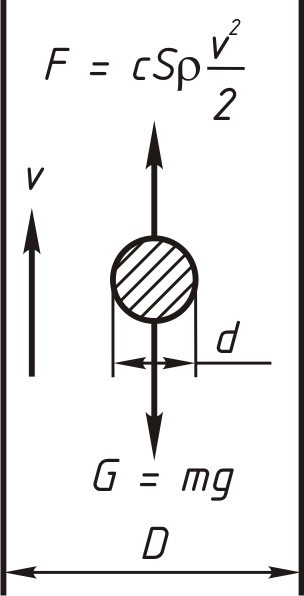 хема сил, действующих на частицу, находящуюся в восходящем потоке:

В зависимости от соотношения этих сил частица может подниматься, опускаться или оставаться неподвижной. Условие равновесия будет наблюдаться в том случае, если F=G. Это случай, так называемого, витания частицы.

Т.е. скорость восходящего потока при котором частица остается статически на одном уровне, находится во взвешенном состоянии:

. (3)

Очевидно, если скорость потока станет равная нулю «0», то частица будет осаждаться со скоростью равной скорости витания, следовательно скорость витания и свободного осаждения частицы равноценны. Т.е. уравнение (3) при известном «с», позволяет определить скорость витания или скорость свободного осаждения частицы, в зависимости от конкретных условий решаемой задачи. Недостаток этого уравнения заключается в неопределенности коэф-та "c", зависящего от Re, который в свою очередь определяются по скорости свободного осаждения или витания частицы. Только в ламинарной области (области действия законов Стокса) при Re<=2, где с= 24/Re.

Ур-е (3) принимает вид: .

За пределами законов Стокса, уравнение (3) обычно решается подбором или графически.