
- •Билет №1.
- •Билет №2
- •1.Методы поиска экстремума заданного функционала качества в системах экстремального регулирования.
- •2 . Введение в закон управления релейных сар воздействий по производной от ошибки регулирования.
- •1. Метод точечных отображений и его применение для исследования процессов
- •2 . Математические модели цифровых систем автоматического управления.
- •Билет №7
- •1. Применение метода точечных отображений для оценки процессов в нелинейных сау. {в лекциях нет!!!}
- •2. Методы построения фазовых портретов нелинейных систем. Небольшое введение:
- •Методы построения фазовых портретов нелинейных систем
- •Билет №8
- •1. Методы построения фазовых портретов нелинейных систем. (смотри билет №7)
- •2. Второй метод оценки устойчивости динамических систем а. М. Ляпунова.
- •Формулировка критерия а.М. Ляпунова (по его первому методу).
- •1. Метод градиента и метод наискорейшего спуска (подъема) в задачах поиска экстремума заданного функционала качества сау.
- •2. Модальный синтез систем автоматического управления.
- •1. Критерий абсолютной устойчивости в. М. Попова.
- •2 . Способы построения фазовых портретов нелинейных систем.
- •Экзаменационный билет № 11
- •Методы настройки промышленных пид-регуляторов.
- •Оценка устойчивости систем с интервально определенными параметрами.
- •Экзаменационный билет № 12
- •Д искретные сау, их разновидности и используемый для их анализа и синтеза математический аппарат.
- •2 . Введение в закон управления релейных сар воздействия по производной от ошибки регулирования.
- •Билет 13.
- •Дискретные d- и z-преобразования и их использование для анализа процессов и состояний в дискретных системах.
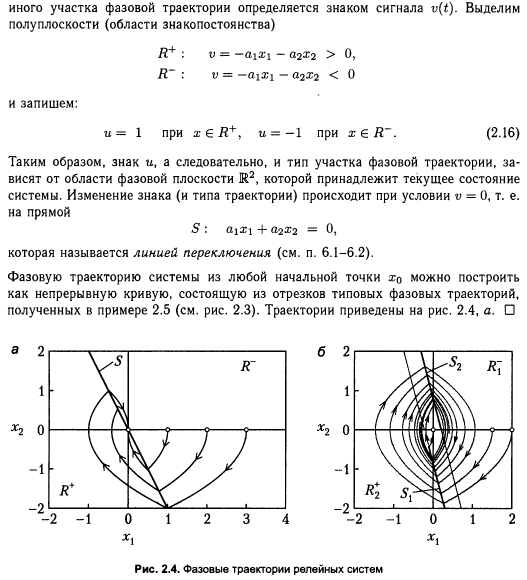
- •Анализ процессов в релейных сар второго порядка методом фазового пространства и оценка влияния типа релейного элемента на характер этих процессов.
- •2 .Обобщение критерия абсолютной устойчивости в. М. Попова на случай неустойчивых и нейтральных систем
- •Экзаменационный билет № 15
- •Метод припасовывания и его применение для исследования релейных систем автоматического управления.
2 .Обобщение критерия абсолютной устойчивости в. М. Попова на случай неустойчивых и нейтральных систем
Д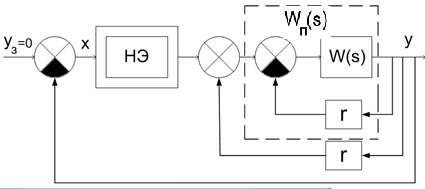 овольно
часто линейн часть бывает нейтральной
или неустойчивой, тогда стараются
преобразовать исследуемую сист и
добиться, чтобы в преобразованной
системе линейн часть была устойчивой.
Нейтральная
– сист, у
которой вход-выходная передаточная
функция имеет несокращающийся сомножитель
s
в знаменателе. Преобразуем:
овольно
часто линейн часть бывает нейтральной
или неустойчивой, тогда стараются
преобразовать исследуемую сист и
добиться, чтобы в преобразованной
системе линейн часть была устойчивой.
Нейтральная
– сист, у
которой вход-выходная передаточная
функция имеет несокращающийся сомножитель
s
в знаменателе. Преобразуем:
П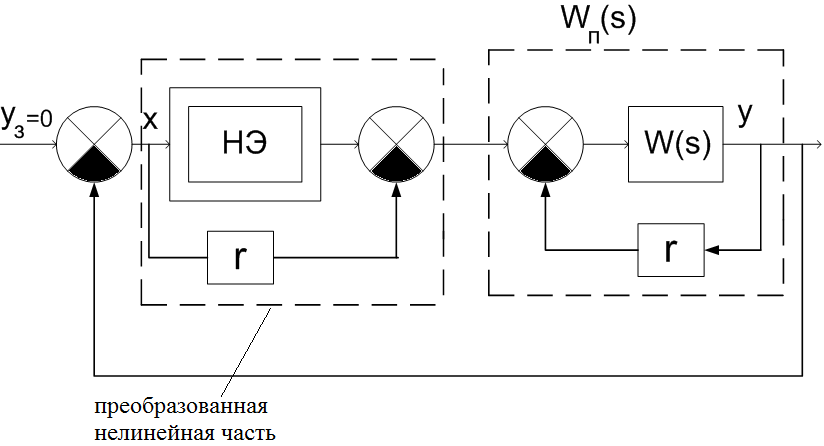 одбираем
по возможности меньшее r,
при котор преобразованная линейн часть
(пунктиром) стала устойчивой. Эквивалентная
(при yз=0):
одбираем
по возможности меньшее r,
при котор преобразованная линейн часть
(пунктиром) стала устойчивой. Эквивалентная
(при yз=0):

 (т.к. параллельная
связь)
(т.к. параллельная
связь)
После
этого можно примен к данной сист критерий
Попова в его прежней редакции, но по
отношению к WП(s)
и ФП(х).
0<Ф(х)-rx<kx;
r<Ф(х)/х<k+r.
Если в исх сист нелинейнсть неоднозначна,
то следует преобразовать схему так, что
преобразованная часть будет иметь
однозначную вход-выходн связь. Если
такое невозможно, то критерий Попова
использовать нельзя. Критерий: Для
устойчивости состояния равновесия
нелинейн сист с однозначной нелинейностью
Ф(х) и устойч линейн частью с W(s),
достаточно выполнение условий: 1.
ReП(jw)=Re[(1+j w)W(jw)+1/k]>
0 2. 0<Ф(х)<kx
или 0<Ф(х)/х<k
w)W(jw)+1/k]>
0 2. 0<Ф(х)<kx
или 0<Ф(х)/х<k
Экзаменационный билет № 15
1.Методы определения непрерывных частей дискретными передаточными функциями и разностными уравнениями.
Описание возможно, когда непрерывная часть системы линейная.

1)
t 2)T
2)T


3)
2T


 i=[0,m]
i=[0,m]
на всем интервале:
 m=[0,∞)
m=[0,∞)
для моментов дискретизации:
 m=[0,∞)
(1)
m=[0,∞)
(1)
по теореме свертки:
y(z)=W(z) x(z)
эквивалентно (1), если W(z)=Z(
x(z)
эквивалентно (1), если W(z)=Z( )
)
W(z) – передаточная функция.
Для соединения идеального ключа и непрерывной части дискретная передаточная функция определяется как Z-преобразование решетчатой функции непрерывной части системы.
Если за ключом стоит совокупность линейных звеньев, то сначала находим эквивалентную им всем передаточную функцию, по ней определяем весовую функцию и по ней решетчатую

2 . Типовые нелинейности в САУ и их математические модели.
Релейные нелинейности двухпозиционные:
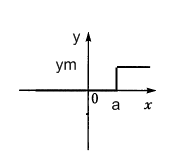
Идеальное
2х позиционное: y=f(x,
![]() )
)

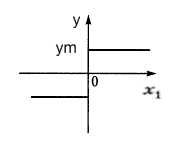
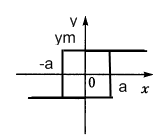
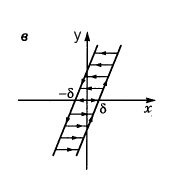
Нелинейность типа «сухое трение» (рис а)
Звено типа насыщения (рис б)
Нелинейность типа «люфт» (рис в)
Нелинейность типа нечувствительность (рис г). Характерно для измерительных и преобразовательных устройств
Нелинейность типа нечувствительность и насыщения (рис д)
Идеальное 3х позиционное реле (рис. е)
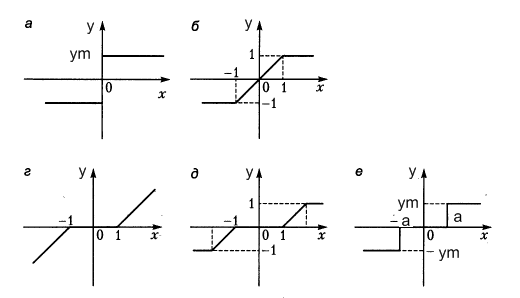
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 16
Метод припасовывания и его применение для исследования релейных систем автоматического управления.
В лекциях вроде нет этого метода, думаю в наших билетах тоже не будет, но всяк случ вот он:
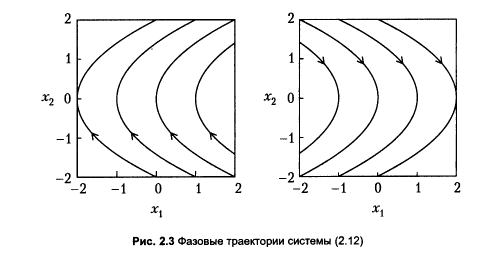
Используется для построения фазовых траекторий линейных систем, решения которых всегда известны, и ряда нелинейных систем с кусочно-постоянными параметрами (системы с негладкими нелинейными звеньями).
Метод
припасовывания предусматривает замену
первоначальной нелинейной системы
более простой моделью с переменной
структурой – линейной моделью с
переключающимися параметрами. Этапы
построения:


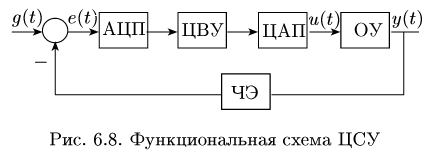
2 . Структурные схемы цифровых и импульсных систем.
Для справки: дискретной называется любая система, у которой хотя бы одна внутренняя или выходная переменная квантованы по времени, по уровню или одновременно и по уровню и по времени.
Если в сау дискретные переменные квантованы только по уровню – релейная система; только по времени – импульсная система; и по времени и по уровню – цифровая система.
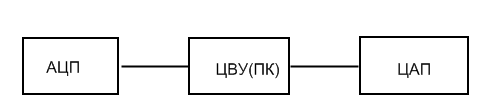
Оно же:
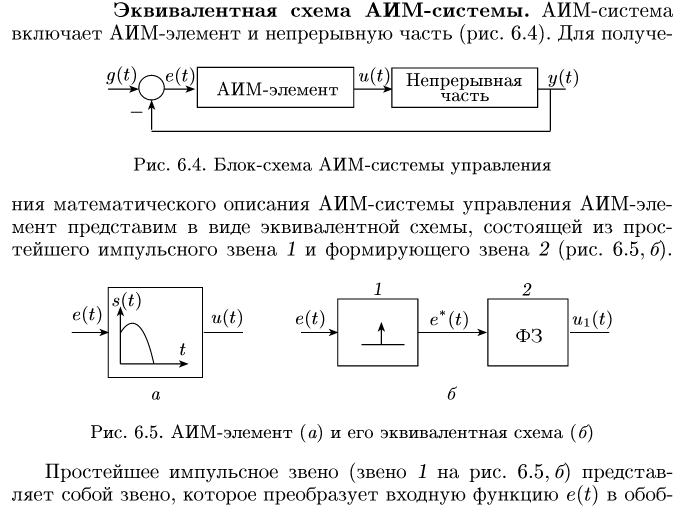
АИМ – амплитудно-импульсная модуляция

