TAU_IDZ_variant_6

Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего образования

«Национальный исследовательский Томский политехнический Университет»

Институт

электронного обучения

140400

Индивидуальное домашнее задание

по дисциплине:

Теория автоматического управления

Исполнитель:
студент группы	З-5 Г2А1		Герасимов А. В.		______________
Руководитель:
преподаватель			Шилин А.А.		________________

Томск - 2016

Задача 1

Составить дифференциальное уравнение в стандартном виде для цепи постоянного тока.

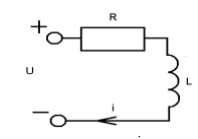
U – входная переменная

I – выходная.

Решение:

По закону Ома:

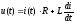
Введем постоянную времени Т:

Т = L/R

Тогда получим:

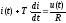
Задача 2

По заданному дифференциальному уравнению выполнить:

1.Записать операторное уравнение в стандартном виде:

2.Получить выражение для передаточной функции.

3.Записать уравнение для ЛАЧХ и ЛФЧХ и построить их

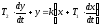
Т₁ = 0,05 Т₂ = 0,2 k = 40

Решение

1. Преобразуем заданное выражение в операторную форму.

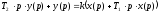
2. Передаточная функция – отношение изображение выходной функции ко входной.

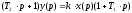
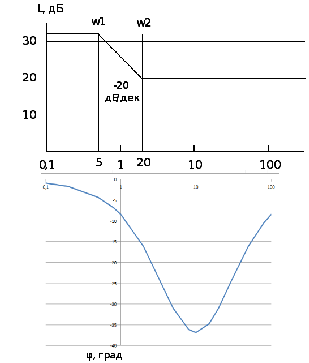
3. Для построения ЛАЧХ запишем уравнения характеристик:

А(w) = |W(p→jw)|

L(w) = 20∙lg(A(w)) = 20∙lg k – 20lg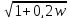 + 20lg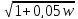

φ(w) = 0 – arctg(0.2∙w) + arctg(0.05w)

Определяем частоты сопряжения ЛЧХ.

w₁ = 1/Т₂ = 1/0,2 = 5 с^-1 (получим наклон -20дБ/дек)

w₂ = 1/Т₁ = 1/0,05 = 20 с^-1 (получим наклон +20дБ/дек)

Усиление на нулевой частоте:

20∙lg(40) = 32 дБ

Задача 3

Для заданной структурной схемы определить передаточные функции замкнутой системы по управлению X(p) (для Z(p) = 0) и по возмущению Z(p) (когда X(p) = 0) и передаточную функцию разомкнутой системы.

Находим передаточную функцию (ПФ) по управлению. С учетом того, что z(p) = 0, то преобразуем внутренний контур с ОС К4.

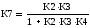
Аналогично преобразуем второй контур.

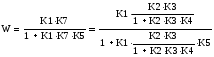
Далее находим ПФ по возмущению. Схема будет иметь вид:

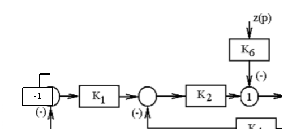
На схеме обозначаем значения функций относительно у(р) и z(p).

Теперь, относительно сумматора (1) можно составить уравнение:

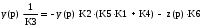
Преобразуем его:

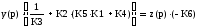
Из него выражаем ПФ по возмущению:

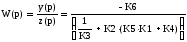
Для определения передаточной функции разомкнутой системы принимаем X(p)=0 и Z(p) = 0, после чего элементы главного замкнутого контура соединяем последовательно.

Получаем схему:

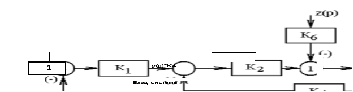ПФ разомкнутой системы:

Задача 4

Оценить устойчивость замкнутой системы по критерию Михайлова.

Значения параметров:

Решение

Запишем уравнение разомкнутой системы:

ПФ замкнутой системы:

Упрощаем:

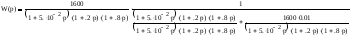
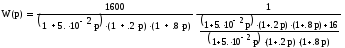
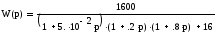
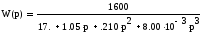
Приводим к нормальному виду:

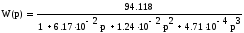
Имеем характеристическое уравнение:

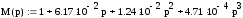
Выполняем подстановку р – jw

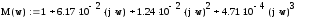
Далее строим годограф на комплексной плоскости:

Годограф, начиная с действительной положительной части оси проходит последовательно 3 квадранта и устремляется в бесконечность. Степень характеристического уравнения также равна 3, значит система устойчива.

Ответы на вопросы:

6. Дать определение статических характеристик по управлению и привести их количественные показатели.

Статическая характеристика — это зависимость между входной (управление) и выходной величинами в установившемся режиме.

Основные показатели:

Передаточный коэффициент – отношение выходной величины ко входной

k = y/x

Порог чувствительности - минимальное значение входной величины, вызывающее изменение выходной величины. Все реальные элементы систем автоматического регулирования имеют порог чувствительности, отличный от нуля.

16. Что можно вычислить по операторному уравнению?

По операторному уравнению можно вычислить передаточную функцию, переходную и весовую функции, характеристики амплитудо-частотная, фазочастотная, годограф (АФЧХ).

26. Перечислить типовые внешние воздействия и дать им характери- стику.

Скачкообразное воздействие – ступенчато изменяющийся сигнал от нуля до определенного значения, например до единицы.

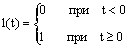
Импульсное воздействие – дельта-функция, ее амплитуда равна бесконечности, а ширина импульса стремится к нулю. Площадь сигнала равна единице.

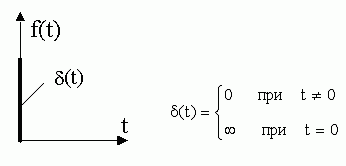
Гармоническое воздействие, имеет постоянную амплитуду и частоту. Описывается уравнением:

x = A∙sin(wt)

36. Перечислить типовые преобразования в структурных схемах

Последовательно соединенные элементы:

Параллельное соединение элементов:

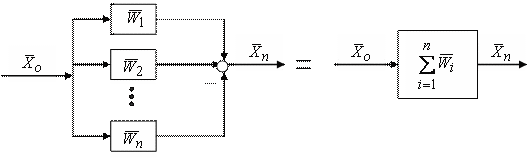
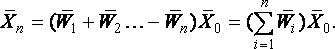
Обратные связи (отрицательные и положительные):

46. Как называется кривая, используемая при оценке устойчивости по Найквисту? Как получить ее уравнение?

Кривая называется годограф или АФЧХ.

Чтобы ее получить необходимо в передаточной функции заменить оператор «р» на «j∙w» (комплекс умножить на частоту).

Далее из полученной частотной характеристики выделить действительную и мнимую часть.

Re(w) = (k∙w ….)

Im(w) = j∙(k∙w ….)

Далее строим зависимость действительной част от мнимой.

56. Какие логарифмические частотные характеристики и для какого состояния системы используются для оценки устойчивости замкнутых систем по критерию Найквиста?

Используются логарифмические АЧХ и ФЧХ. Строятся характеристики для разомкнутых систем. По виду эих характеристик и определяют устойчивость замкнутой системы.

66. Назначение и понятие коррекции.

Если при разработке/исследовании какой-либо системы она получилась неустойчивой (либо запас устойчивости недостаточен) в систему вводят корректирующее звено. Коррекция может быть параллельной, последовательной. Корректирующее звено оказывает влияние на характеристики всей системы, изменяя те ее показатели, которые влияют на устойчивость, качество регулирования.

76. Понятие расчетной структурной схемы нелинейной системы. Принцип ее составления.

Большая группа точных и приближенных методов исследования автоматических систем на основе нелинейного подхода использует типовую структурную схему, приведенную на рисунке.

В качестве дополнительного ограничения этого расчетного вида математических моделей обычно принимают безынерционность единственного нелинейного элемента с одним входом и одним выходом.

Динамические свойства системы сосредоточены в линейной части с передаточной функцией

По структурной схеме запишем систему уравнений:

 

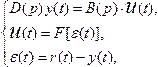
где  - оператор дифференцирования.

Для автономной системы воздействие тождественно равно нулю, тогда уравнения приводятся к виду 

Уравнения линейной части в форме пространства состояний при условии m<n имеют вид

 

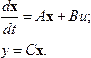
 С учетом нелинейного элемента для автономной системы получим следующие уравнения:

 

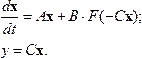
Если структурная схема исследуемой системы отличается от расчетной, то в некоторых случаях ее можно преобразовать в расчетную форму. Проблема заключается в том, что в случае нелинейных моделей не всегда применимы правила структурных преобразований линейных систем.

Литература

1. Зайцев А.П. Теория автоматического управления: Учебное по- собие. – Томск: Изд. ТПУ, 2005. – 155 с

2. Расчет автоматических систем / Под ред. А.В. Фатеева. – М.: Высшая школа, 1973.

3. Теория автоматического управления / Под ред. Воронова А.А. Ч. 1. М.: Высшая школа, 1986.– 367 с.

16