
- •Билет №1.
- •Билет №2
- •1.Методы поиска экстремума заданного функционала качества в системах экстремального регулирования.
- •2 . Введение в закон управления релейных сар воздействий по производной от ошибки регулирования.
- •1. Метод точечных отображений и его применение для исследования процессов
- •2 . Математические модели цифровых систем автоматического управления.
- •Билет №7
- •1. Применение метода точечных отображений для оценки процессов в нелинейных сау. {в лекциях нет!!!}
- •2. Методы построения фазовых портретов нелинейных систем. Небольшое введение:
- •Методы построения фазовых портретов нелинейных систем
- •Билет №8
- •1. Методы построения фазовых портретов нелинейных систем. (смотри билет №7)
- •2. Второй метод оценки устойчивости динамических систем а. М. Ляпунова.
- •Формулировка критерия а.М. Ляпунова (по его первому методу).
- •1. Метод градиента и метод наискорейшего спуска (подъема) в задачах поиска экстремума заданного функционала качества сау.
- •2. Модальный синтез систем автоматического управления.
- •1. Критерий абсолютной устойчивости в. М. Попова.
- •2 . Способы построения фазовых портретов нелинейных систем.
- •Экзаменационный билет № 11
- •Методы настройки промышленных пид-регуляторов.
- •Оценка устойчивости систем с интервально определенными параметрами.
- •Экзаменационный билет № 12
- •Д искретные сау, их разновидности и используемый для их анализа и синтеза математический аппарат.
- •2 . Введение в закон управления релейных сар воздействия по производной от ошибки регулирования.
- •Билет 13.
- •Дискретные d- и z-преобразования и их использование для анализа процессов и состояний в дискретных системах.
- •Анализ процессов в релейных сар второго порядка методом фазового пространства и оценка влияния типа релейного элемента на характер этих процессов.
- •2 .Обобщение критерия абсолютной устойчивости в. М. Попова на случай неустойчивых и нейтральных систем
- •Экзаменационный билет № 15
- •Метод припасовывания и его применение для исследования релейных систем автоматического управления.
Дискретные d- и z-преобразования и их использование для анализа процессов и состояний в дискретных системах.
Дискретное
D-преобразование
ставит в соответствие решение соответствие
решетчатой функции х[nT]
ее изображение x(q),
при этом прямое D-преобр
опр-ся формулой:
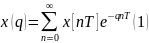 -прямое D-преобразование.
-прямое D-преобразование.
 –обратное D-преобразование.
Это формулы дискретного преобразования
Лапласа. Это преобразование имеет один
ограничитель. Обратное преобразование
можно определить только когда все полюса
x(q)=B(q)/A(q)
{A(q)=0}
расположены в полосе:
–обратное D-преобразование.
Это формулы дискретного преобразования
Лапласа. Это преобразование имеет один
ограничитель. Обратное преобразование
можно определить только когда все полюса
x(q)=B(q)/A(q)
{A(q)=0}
расположены в полосе:
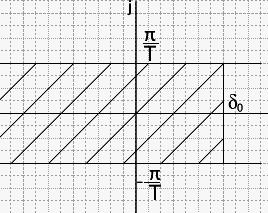
Во
многих случаях δ0
может быть равно 0. В практике чаще
используют не D-преобр,
а Z-преобр.
Z-преобр
опр-ся след выражен:
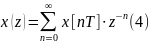 – прямое Z-преобразование.
Z-преобр
получ-ся из D-преобр
заменой: z=eqT
(5).
– прямое Z-преобразование.
Z-преобр
получ-ся из D-преобр
заменой: z=eqT
(5).
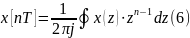 обратное Z-преобр.
Преобразования позвол нам решать сист
дифф уравн операторными методами
(работать с алгебраич уравн). D
и Z
преобр, также как и непрер преобр Лапласа,
использ-ся для упрощения решения
разностных уравнений относительно
интересующих нас переменных систем.
Тем самым мы от разностных уравн переходим
к обычн алгебраическим. В операторных
преобразованиях использ целый ряд
теорем: 1. Теорема линейности: Пусть
обратное Z-преобр.
Преобразования позвол нам решать сист
дифф уравн операторными методами
(работать с алгебраич уравн). D
и Z
преобр, также как и непрер преобр Лапласа,
использ-ся для упрощения решения
разностных уравнений относительно
интересующих нас переменных систем.
Тем самым мы от разностных уравн переходим
к обычн алгебраическим. В операторных
преобразованиях использ целый ряд
теорем: 1. Теорема линейности: Пусть
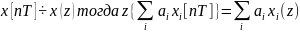 2. Теор о начальном значении:
2. Теор о начальном значении:
 3. Теор о конечном значении:
3. Теор о конечном значении:
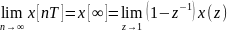 4. Теор о смещении в области оригиналов:
4. Теор о смещении в области оригиналов:
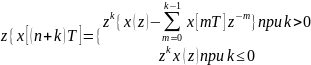
5.
Теор о смещении в области изображений:
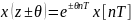 6. Теор о суммах решетчатых функций
6. Теор о суммах решетчатых функций
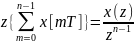 7.
Изображение
разности решетчатых функций
7.
Изображение
разности решетчатых функций
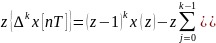 8. Теор свертки
8. Теор свертки
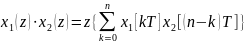 .
Эти формулы позволяют перейти от
разностных уравн к их аналогам (операторным
уравн). Для ЦВУ:
.
Эти формулы позволяют перейти от
разностных уравн к их аналогам (операторным
уравн). Для ЦВУ:
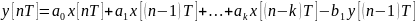
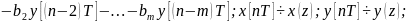
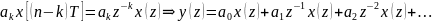
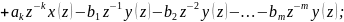
[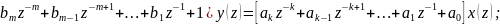
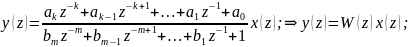
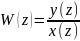 Отношение
Z-преобр
выходного сигнала и входн сигнала
дискретной системы при нулевых начальн
условиях назыв дискретной передаточной
функцией этой системы. Многомерную по
входу и выходу линейную дискретную
систему можно характеризовать
совокупностью дискретных передаточных
функций
Отношение
Z-преобр
выходного сигнала и входн сигнала
дискретной системы при нулевых начальн
условиях назыв дискретной передаточной
функцией этой системы. Многомерную по
входу и выходу линейную дискретную
систему можно характеризовать
совокупностью дискретных передаточных
функций
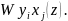 Эту
совокупность можно записать в упорядоч
форме в виде дискретн передаточной
матрицы системы.
Эту
совокупность можно записать в упорядоч
форме в виде дискретн передаточной
матрицы системы.
Анализ процессов в релейных сар второго порядка методом фазового пространства и оценка влияния типа релейного элемента на характер этих процессов.
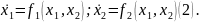 В
пространстве х1,
х2
делим одно уравн на 2ое.
В
пространстве х1,
х2
делим одно уравн на 2ое.
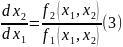 уравн фазовых
траекторий в диффер форме. Для получения
уравн (3) в явной форме, его надо
проинтегрировать. х2=f(x1)+C
(4); C-постоянная
интегрирования. Найдем по (4) уравн
фазовой траектории, проходящ через
конкретную точку х10,
х20.
Для этого подставляем эти значения
вектора х в уравн (4): х20=f(x10)+C
(5) , C=x20-f(x10)
(6). Находим С, соотв-щую фазовой траектории,
проходящей через точку х10,
х20. Подставляем
найденной С из (6) в уравн (4): х2=f(x1)+x20-f(x10)
– уравн фазовой траектории данной сист,
проходящ через х10,
х20. По
этому уравн, принимая различн знач х1,
мы находим соотв-щие х2
и можем построить график в фазовом
пространстве х1,
х2
, т.е. построить интересующую нас фазовую
траекторию. Уравн (7) может исп-ся для
построения семейства фазов траекторий,
проходящих через выбранные точки с
конкретными х10,
х20.
уравн фазовых
траекторий в диффер форме. Для получения
уравн (3) в явной форме, его надо
проинтегрировать. х2=f(x1)+C
(4); C-постоянная
интегрирования. Найдем по (4) уравн
фазовой траектории, проходящ через
конкретную точку х10,
х20.
Для этого подставляем эти значения
вектора х в уравн (4): х20=f(x10)+C
(5) , C=x20-f(x10)
(6). Находим С, соотв-щую фазовой траектории,
проходящей через точку х10,
х20. Подставляем
найденной С из (6) в уравн (4): х2=f(x1)+x20-f(x10)
– уравн фазовой траектории данной сист,
проходящ через х10,
х20. По
этому уравн, принимая различн знач х1,
мы находим соотв-щие х2
и можем построить график в фазовом
пространстве х1,
х2
, т.е. построить интересующую нас фазовую
траекторию. Уравн (7) может исп-ся для
построения семейства фазов траекторий,
проходящих через выбранные точки с
конкретными х10,
х20.
Билет №14. 1. Влияние чистого запаздывания и введение в закон управления производных от ошибки регулирования в релейных САР.
а) Чистое запаздывание в объекте управления в релейных сист автом регулирования приводит к наклону вправо линий переключения и значит к повышению колебательности системы, к ухудшению динамики в целом. Для улучшения динамики таких сист можно использовать в законе управления ПД алгоритм формирования входного сигнала на реле.

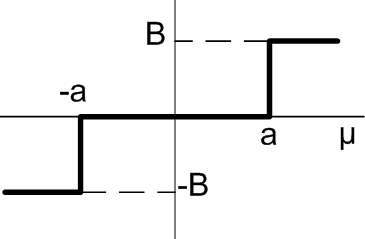
х+ρ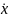 =х+ρу=
=х+ρу=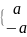 ;
x+ρy=a;
y=
;
x+ρy=a;
y=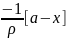
В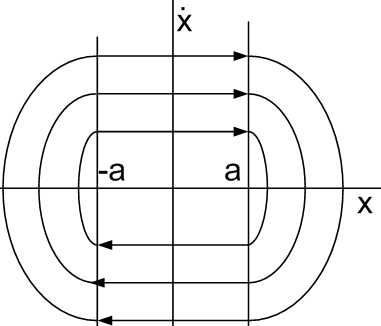 ведение
производной улучшает динамику, снижает
колебания. W(s)=1+ρs;
ведение
производной улучшает динамику, снижает
колебания. W(s)=1+ρs;
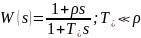 .
Реализуют
с использованием упругих дифференцирующих
звеньев. При очень больших ρ в сист могут
наступить скользящие режимы (когда
изображающая точка попадает на линию
переключения, а дальше она в идеальном
толковании движется по линии переключения
или около нее):
.
Реализуют
с использованием упругих дифференцирующих
звеньев. При очень больших ρ в сист могут
наступить скользящие режимы (когда
изображающая точка попадает на линию
переключения, а дальше она в идеальном
толковании движется по линии переключения
или около нее):
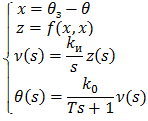 б)
б)
(1) Полагаем,что будем исследовать только собственные движения (все входн воздействия =0),
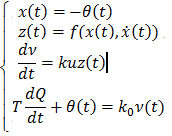 т.е.
т.е.
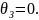 В символич операторной форме:
В символич операторной форме:
(2) Составим уравн собств движений этой сист, записанное относительно шибки регулирования.
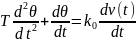 Подставим сюда
Подставим сюда
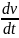 из (2) и z(t).
из (2) и z(t).
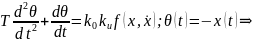
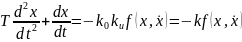
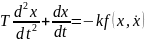 (3) – уравн собств
движ данн сист относительно ошибки
регулирования х.
(3) – уравн собств
движ данн сист относительно ошибки
регулирования х.
