Билет №1

Правило умножения матриц

Пусть даны 2 матрицы A(m×n) и B(n×l), причем число столбцов матрицы A равно числу строк матрицы B. Тогда матрица C(m×l) с элементами , (т.е. i-тая строка матрицы A, умноженная скалярно на j-й столбец матрицы B, дает c_ij-й элемент матрицы C, стоящий в i-й строке и j-м столбце).

, .

Билет №2

Свойство системы линейных уравнений, содержащей тривиальное уравнение.

Тривиальное уравнение – уравнение, в котором коэффициенты при всех неизвестных и свободных членах равны нулю.

Теорема: Система линейных уравнений, содержащая тривиальное уравнение, равносильна той же системе без тривиального уравнения.

Доказательство: Рассмотрим СЛУ (1) и ту же СЛУ (2), но без тривиального уравнения.

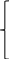
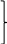
(1) ……………………………………………………………… (2)

Пусть вектор является решением системы (1), тогда этот вектор является и решением системы (2).

Обратно, пусть вектор является решением системы (2). Т.к. n-мерный вектор L является и решением тривиального уравнения, то он является решением системы (1).

Таким образом, система линейных уравнений, содержащая тривиальное уравнение, равносильна этой же системе без тривиального уравнения.

Билет №3

Свойство свободных неизвестных в разрешенной СЛУ

СЛУ называется разрешенной, если каждое уравнение системы содержит хотя бы одно разрешенное неизвестное.

Теорема: Если в разрешенной СЛУ (4) придать свободным неизвестным произвольные значения , т. е. , то найдется единственное решение этой системы в виде n-мерного вектора К, у которого значения координат, соответствующих свободным неизвестным, равны соответственно .

Доказательство:

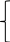
(4)

Подставим в систему (4). Тогда разрешенные неизвестные примут значения такие, что:

(5)

Т. к. вектор обращает каждое уравнение системы (4) в точное числовое равенство, то он является решением этой системы. Таким образом, доказано существование решения системы (4).

Докажем единственность такого решения. Пусть вектор с теми же значениями свободных неизвестных является также решением системы (4). Тогда подставим его в систему (4), получим:

(6)

Сопоставляя (5) и (6), видим, что . Таким образом, доказано, что существует единственное решение системы (4) с заданными значениями свободных неизвестных.

Замечания:

1. Т. к. значения свободных неизвестных можно задать бесконечно большим числом способов, то система (4) является неопределенной.

2. Разрешенная СЛУ всегда совместна. При этом она определена, если m=n, т. е. число уравнений равно числу неизвестных, и не определена, если число уравнений меньше числа неизвестных, т. е. m<n

Билет №4

Элементарные преобразования СЛУ

-умножение обеих частей любого ур. исх.сис на число, не равное 0

-замена i-го уравнения в сис (1) АiX+АjX=bi+bj позволяет переходить от исодной СЛУ к равносильной

-Жорданово преобразование