
- •1. Понятие о первообразной и неопределенном интеграле.
- •2. Основные свойства неопределенного интеграла.
- •3. Основные методы интегрирования. Метод замены переменной интегрирования.
- •4. Основные методы интегрирования. Интегрирование по частям.
- •5. Интегрирование простейших иррациональностей.
- •6. Понятие определенного интеграла.
- •7. Геометрический смысл определенного интеграла.
- •8. Основные свойства определенного интеграла.
- •9. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •11. Несобственные интегралы с бесконечными пределами интегрирования. Несобственные интегралы с бесконечными пределами интегрирования
- •22. Решение линейного неоднородного дифференциального уравнения методом вариации произвольных постоянных.
- •28. Понятие знакочередующегося ряда. Теорема Лейбница.
- •31. Классическое определение вероятности.
- •32. Свойства вероятности.
- •33. Понятие относительной частоты. Статистическая вероятность.
- •34. Геометрические вероятности.
- •35. Основные формулы комбинаторики.
- •36. Теоремы сложения вероятностей.
- •37. Теоремы умножения вероятностей.
- •38. Формула полной вероятности.
- •39. Вероятность гипотез. Формулы Бейеса.
- •40. Повторение испытаний. Формула Бернулли.
- •41. Повторение испытаний. Локальная теорема Лапласа.
- •42. Повторение испытаний. Интегральная теорема Лапласа.
- •45. График функции распределения.
- •46. Плотность распределения вероятностей нсв. Свойства плотности распределения.
- •47. Нахождение функции распределения по известной плотности распределения.
- •48. Математическое ожидание дсв.
- •49. Свойства математического ожидания. Математическое ожидание числа появлений события в независимых испытаниях.
- •50. Дисперсия дискретной случайной величины.
- •51. Свойства дисперсии. Дисперсия числа появлений события в независимых испытаниях.
- •52. Числовые характеристики непрерывных случайных величин.
- •53. Понятие о теоретических моментах распределения.
- •Влияние параметров нормального распределения на форму нормальной кривой.
- •81. Статистическая проверка параметрических гипотез. Ошибки первого и второго рода. П.2. Ошибки первого и второго рода.
- •Проверка гипотез равенства математических ожиданий двух случайных величин (большие независимые выборки).
- •89. Геометрическая интерпретация и графическое решение злп.
- •90. Понятие симплексного метода.
- •91. Понятие двойственности. Построение пары взаимно двойственных
- •92. Первая теорема двойственности и ее экономическое содержание.
- •93. Вторая теорема двойственности и ее экономическое содержание.
- •1. Понятие о первообразной и неопределенном интеграле.
- •2. Основные свойства неопределенного интеграла.
- •3. Основные методы интегрирования. Метод замены переменной интегрирования.
9. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
Пусть
f(x)
– интегрируемая на отрезке
функция, тогда для любого
она будет интегрируема и на отрезке от
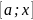 .
Рассмотрим интеграл
.
Рассмотрим интеграл
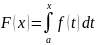 являющийся функцией верхнего предела
x.
В этом равенстве использована переменная
интегрирования t
с тем, чтобы отличить ее от верхнего
предела интегрирования.
являющийся функцией верхнего предела
x.
В этом равенстве использована переменная
интегрирования t
с тем, чтобы отличить ее от верхнего
предела интегрирования.
Теорема.
Если f(x)
– непрерывна на
функция и имеет место равенство
,
то
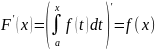 ,
т.е. производная от интеграла с переменным
верхним пределом интегрирования равна
значению подынтегральной функции в
точке, равной верхнему пределу. Эту
теорему можно переформулировать
следующим образом: если функция f(x)
непрерывна на отрезке
,
то функция
является ее первообразная на
.
Следовательно,
.
,
т.е. производная от интеграла с переменным
верхним пределом интегрирования равна
значению подынтегральной функции в
точке, равной верхнему пределу. Эту
теорему можно переформулировать
следующим образом: если функция f(x)
непрерывна на отрезке
,
то функция
является ее первообразная на
.
Следовательно,
.
Формула Ньютона-Лейбница
Теорема.
Если функция f(x)
непрерывна на отрезке
и F(x)
– какая-либо ее первообразная, то
справедлива формула
Ньютона-Лейбница:
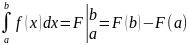 .
.
10.
Замена переменной и интегрирование по
частям в определенном интеграле.
Теорема. Пусть функция f(x)
непрерывна на отрезке
,
а функция
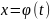 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке
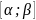 ,
причем отрезок
является множеством значений функции
и
,
причем отрезок
является множеством значений функции
и
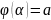 ,
,
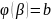 .
Тогда справедлива формула:
.
Тогда справедлива формула:
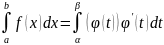 .
Эта формула называется формулой
замены переменной в
определенном интеграле.
.
Эта формула называется формулой
замены переменной в
определенном интеграле.
Теорема.
Если функции u(x)
и v(x)
имеют непрерывные производные на отрезке
,
то справедлива формула:
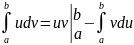 .
Эта формула называется формулой
интегрирования по частям в
определенном интеграле.
.
Эта формула называется формулой
интегрирования по частям в
определенном интеграле.
11. Несобственные интегралы с бесконечными пределами интегрирования. Несобственные интегралы с бесконечными пределами интегрирования
Пусть
функция f(x)
определена на промежутке и интегрируема
на любом отрезке
,
где
 .
.
Несобственным
интегралом с бесконечным верхним
пределом интегрирования от
функции f(x)
называется
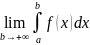 ,
который обозначают символом:
,
который обозначают символом:
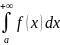 .
Таким образом по определению
.
Таким образом по определению
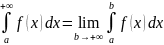 .
.
Если конечен, то несобственный интеграл называют сходящимся, в противном случае – расходящимся.
Аналогично
вводятся несобственные интегралы:
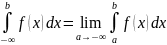 ,
,
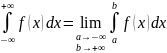 .
.
12.
Несобственные интегралы от неограниченных
функций.
Предположим, что функция f(x)
определена на промежутке
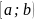 и не ограничена при
и не ограничена при
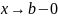 ,
т.е.
,
т.е.
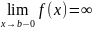 .
.
Б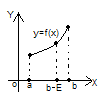 удем
считать, что для любого сколь угодно
малого числа Е
удем
считать, что для любого сколь угодно
малого числа Е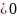 на отрезке
на отрезке
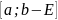 функция f(x)
интегрируема, т.е. существует
функция f(x)
интегрируема, т.е. существует
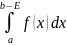 .
.
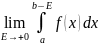 называют
несобственным
интегралом от неограниченной функции
f(x)
на промежутке
и обозначают символом
называют
несобственным
интегралом от неограниченной функции
f(x)
на промежутке
и обозначают символом
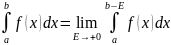 .
.
Аналогично,
если f(x)
не ограничена при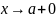 ,
то положим
,
то положим
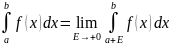 .
.
Если
же не ограничена при
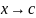 ,
,
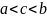 ,
то
,
то
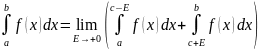 .
.
Несобственный
интеграл от неограниченной функции
называют сходящимся,
если предел
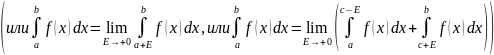 конечный, в противном случае интеграл
называют расходящимся.
конечный, в противном случае интеграл
называют расходящимся.
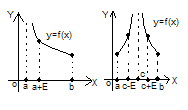
13. Дифференциальные уравнения первого порядка. Общие понятия. ДУ называется ур-е связывающее независимые переменные, их функцию и производные этой функции.
Если неизвестная функция зависит только от одной переменной , то ДУ называется обыкновенным.
Если же неизвестная функция зависит от нескольких переменных и ДУ содержит её частные производные по этим переменным , то ДУ называем уравнением частных производных .
Порядком ДУ называется наивысший порядок производной, входящей в это ур-е.
Обыкновенное ДУ первого порядка имеет вид: F(x,y,y’)=0 (17.1)
Или в разрешённом относительно y’ виде : y’=f(x,y) (17.2)
Решением ДУ называется такая дифференциальная функция y=y(x), которая при подстановке в уравнение обращает его в тождество , например: F(x,y(x),y’(x))=0 или y’(x)=f(x,y(x))
Процесс нахождения всех решений ДУ называется инрегрированием , график решения y=y(x) ДУ называется гистегральной прямой.
Задачи Коши для ДУ первого порядка состоит в нахождении решения y=ϕ(x)данного ДУ , удовлетворяющих начальному условию y(x)=y’.
Общим решением ДУ первого порядка называется функция y=ϕ(x,C), обладающая следующим свойствами:
Она является решением данного уравнения при любых значениях постоянной С принадлежащих некоторому множеству.
Для любого начального условия существует единственное значение С=С0 , при котором функция y=ϕ(x, С0)удовлетворяет заданному начальному условию y(x0)=y0
Решением ДУ, выраженное в неявной форме, называется общим интегралом ур-я.
Общий интеграл имеет вид Ф(х,у,С)=0
Частным решением ДУ называется решение, полученное из общего решения при конкретном значении С: y=ϕ(x, С0)
Аналогично определяется частный интеграл Ф(х,у,С0)=0
Встречаются
ДУ имеющие решения которые не получаются
из общего решения ни при каких значениях
С (в том числе и при С=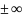 ).
Такие решения называются особыми.
).
Такие решения называются особыми.
14. Дифференциальные уравнения с разделяющимися переменными. Пример. Определение 17,1
Ур-е вида М1(х)М2(у)dx+N1(x)N2(y)dy=0 17.3
Называется
ур-е с разделяющимися переменными.
Предположив , что N1(x)N2(y)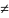 0,
и разделив на это произведение обе части
ур-я (17,3) получим ур-е:
0,
и разделив на это произведение обе части
ур-я (17,3) получим ур-е:
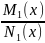 dx+
dx+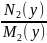 dy=0
17.4
dy=0
17.4
Которое называется ур-ем с разделёнными переменными .
Интегрируя
обе части ур-я (17,4), находим общий интеграл
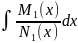 +
+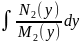 =С
=С
Действительные
корни ур-й N1(x)=0,
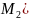 )=0
является решениями исходного ур-я. Эти
решения , и только они, могут оказаться
особыми.
)=0
является решениями исходного ур-я. Эти
решения , и только они, могут оказаться
особыми.
Пример 17,1. Найти общее решение ДУ
Хуdx+(x+1)dy=0
Решение .
Это
ур-е с разделяющимися переменными.
Разделив данное ур-е на произведение
y(x+1)
0,
получим:
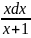 +
+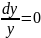
Интегрируя обе части полученного ур-я, имеем:
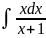 +
+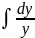 =ln
=ln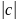 ,
,
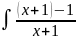 dx+
=
ln
,
откуда
dx+
=
ln
,
откуда
x-ln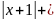 ln
ln =ln
=ln ,
,
xlnC-ln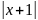 +ln
=ln
,
+ln
=ln
,
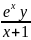 =C
=C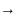 y=C(x+1)e-x
–общее решение исходного ур-я
y=C(x+1)e-x
–общее решение исходного ур-я
15.
Однородные дифференциальные уравнения
первого порядка (определение, метод
решения).
Опред.17.2 Функция
φ(х,y)
называется однородной
функцией
n-го
измерения относительно переменных x,
y,
если для любого t€R
выполняется тождество φ(tx,
ty)=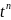 , где t€Z.
, где t€Z.
Опред. 17.3 ДУ вида M(x,y)dx+N(x,y)dy=0 (17.5)
Называется однородным, если М(х,у) и N(х,у) – однородные функции одного измерения.
Это уравнение всегда может быть приведено к виду:
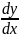 =φ
=φ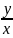
С помощью подстановки у=uх или (х=uу), где u=u(x), однородное уравнение преобразуется к уравнению с разделяющимися переменными.
При этом y’=u’x+u(или dy=xdu+udx)
Пример17.2.Решить
уравнение y‘=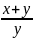
Решение. Имеем y‘=1+
Представим y=ux, y‘=u‘x+u, получим уравнение с разделяющимися переменными: u‘x+u=1+u => u‘x=1 или xdu=dx.
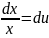
Интегрируя последнее уравнение и подставляя (y/x) вместо u, находим общее решение исходного уравнения:
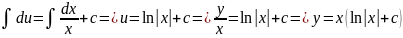 .
.
16. Линейные дифференциальные уравнения первого порядка (определение, методы решения). Определение 17.4. Уравнение вида y’+P(x)y=Q(x) (или A(x)y’+B(x)=C(x)(17.6) называются линейным ДУ.
При этом уравнение: y’+P(x)=0, в котором правая часть тождественно равна нулю, называется линейным однородным, а уравнение 17.6, в котором Q(x)≠0 – линейным неоднородным.
Общее
решение уравнения 17.7 имеет вид: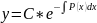
Общее решение неоднородного линейного уравнения, можно найти одним из следующих методов:
Метод вариации произвольной постоянной (Лагранжа), состоит в том, что сначала находят общее решение M(x,y)dx+N(x,y)dy=0 соответственно линейного однородного уравнения. Затем, варьируя произвольную постоянную,т.е.: полагая
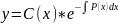 и подставляя y
в уравнение 17.6 получаем C’(x)*
и подставляя y
в уравнение 17.6 получаем C’(x)*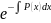 =Q(x).
Из последнего уравнения определим
С(х): С(х)=
=Q(x).
Из последнего уравнения определим
С(х): С(х)=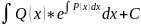 .
Следовательно общее решение неоднородного
линейного уравнения имеет вид: у=
(
)
.
Следовательно общее решение неоднородного
линейного уравнения имеет вид: у=
(
)Метод подстановки заключается в том, что с помощью подстановки y=u(x)v(x), где u,v – неизвестные функции, уравнение 17.6 к виду: u’v+uv’+P(x)uv=Q(x) Следовательно
u’v+u(v’+P(x)v)=Q(x).
Так
кА одна из функций выбирается произвольно,
тогда функция u(x)
определяется из уравнения u’(x)v(x)=Q(x),
u(x)=Q(x)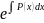 dx+C
dx+C
Метод интегрирующего множителя (метод Эйкера) Обе части уравнения 17.6. умножим на интегрирующий множитель µ= . В результате получим: y’ +P(x)y =Q(x) .
Общее решение полученного уравнения имеет вид:
Y= ( )
17. Дифференциальные уравнения высших порядков. Общие понятия. Дифференциальное уравнение n-го порядка называют уравнение вида
Y(n)=f(x,y,y`,…,y(n))=0 (18.1)
Или
F(x,y,y`,…,y(n))=0 (18.2)
Решением такого уравнения будет всякая n раз дифференцированная функция y=u(x),обращающая уравнение (18.1) или (18.2) в тождества. Задача Коши для дифф.ур-я (18.1) состоит в том, чтобы найти такое решение этого уравнения, которое удовлетворяет начальное условие:
Y(x0)=y0 , y`(x0)=y`0 , y``(x0)=y``0 ,…, y(n-1)(x0)=y0(n-1), (18.3)
Где y0, y`0, y``0, y0(n-1) – заданные числа(некоторые начальные условия).
Общим решением уравнения (18.1) или (18.2) называется функция
Y=µ(x,C1,C2,…,Cn) (18.4)
Которая при любых значениях произв. постоянных C1,C2,…,Cn является решением этого дифф.ур-я и при соответствующем выборе произв. постоянных C1,C2,…,Cn будет решением любой задачи Коши, поставленной для данного уравнения.
Общим интегралом уравнения (18.1) или (18.2) называется соотношение вида
Ф(x,C1,C2,…,Cn)=0 (18.5)
Неявно определяющее общее решение этого уравнения.
Частным решением(интегралом) уравнения (18.1) или (18.2) называется всякое решение, получаемое из общего при конкретных значениях постоянных C1,C2,…,Cn.
18.
Уравнение вида
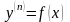 .
Уравнение вид
.
Уравнение вид
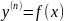 .
.
Общее решение данного уравнения получается n-кратным интегрированием:
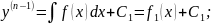
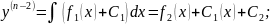
…………………………………………………………………
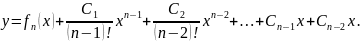
Где
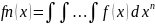 .
.
Пример
18.1 Найти общее решение уравнения : y’’’
=
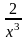
Решение :
y’’
= 2 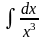 =
-
=
-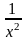 + C1
+ C1
y’
=
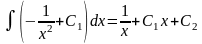
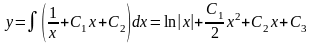
Таким образом общее решение исходного уравнения имеет вид :
y
=
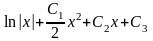
19.
Уравнения вида
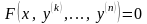 ,
не содержащие искомой функции и ее
производных
,
не содержащие искомой функции и ее
производных
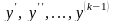 .
Данное
ур-ие с помощью замены y(k)
=
p(x)
можно свести к ур-ию порядка n-k:
F(x,
p,
p’,…,p(n-k))=0
.
Данное
ур-ие с помощью замены y(k)
=
p(x)
можно свести к ур-ию порядка n-k:
F(x,
p,
p’,…,p(n-k))=0
Предположим, что для полученного ур-ия найдено общее решение
p(x)=φ(x, c1, c2,…,cn-k)
Тогда искомую ф-ию y(x) можно получить путем k-кратного интегрирования ф-ии р(х)
Простейшим из таких ур-ий имеет вид
F(x, y’, y”)=0 или y”=f(x, y’)
С помощью подстановки y’=p(x) его сводят к ур-ию 1-го порядка
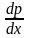 =f(x,
p)
с неизвестной функцией р, а затем из
ур-ия y’=p(x)
находят у.
=f(x,
p)
с неизвестной функцией р, а затем из
ур-ия y’=p(x)
находят у.
Пример 18.2. Найти частное решение ур-ия
y”- =
x(x-1),
y(2)=1,
y’(2)=
-1
=
x(x-1),
y(2)=1,
y’(2)=
-1
Решение. Это ур-ие вида y”=f(x, y’).
Полагая y’=p(x), y”= (y”=p’(x)), получаем линейное дифференциальное ур-ие 1-го порядка относительно неизвестной ф-ии р(х):
p’-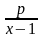 =
x(x-1).
=
x(x-1).
Полагая
в последнем ур-ии p=uv,
p’=u’v+uv’,
получаем u’v+uv’-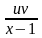 =х(х-1)
или u’v+u(v’-
=х(х-1)
или u’v+u(v’-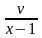 )
= x(x-1).
Определяем v(x),
полагая
)
= x(x-1).
Определяем v(x),
полагая
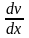 -
=0
или
=
,
-
=0
или
=
,
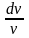 =
=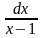 ;
;
Интегрируем
последнее ур-ие: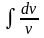 =
=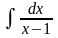
Тогда
ln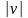 =ln
=ln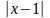 или v=x-1.Определим
u(x)
из ур-ия u’(x-1)=x(x-1),
u’=x,
u=
или v=x-1.Определим
u(x)
из ур-ия u’(x-1)=x(x-1),
u’=x,
u=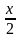 +C1
+C1
След.,
р=(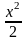 +С1)(х-1)=
+С1)(х-1)=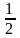 (x3-x2)+C1x-C1.Возвращаясь
к переменной у, имеем:
(x3-x2)+C1x-C1.Возвращаясь
к переменной у, имеем:
y’=
(x3-x2)+C1x-C1,
y=
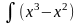 dx
+
dx
+
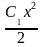 -
C1x+C2
=
(
-
C1x+C2
=
(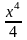 -
-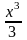 )+
-
C1x+C2
=
)+
-
C1x+C2
=
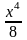 -
-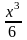 +
-
C1x+C2
+
-
C1x+C2
Т.о., общее решение исходного ур-ия имеет вид:
у= - + - C1x+C2.
Воспользовавшись начальным условием, получаем систему
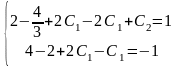
откуда
С2= , С1=
-3
, С1=
-3
След.,
частное решение исходного ур-ия имеет
вид у=
-
-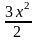 +3х+
.
+3х+
.
20.
Уравнения вида
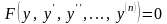 ,
не содержащие независимой переменной.
18.4 Ур-ия вида F(y,
y’,
y”,
y(n))=0,
не содержащие независимой переменной
,
не содержащие независимой переменной.
18.4 Ур-ия вида F(y,
y’,
y”,
y(n))=0,
не содержащие независимой переменной
Если положить y’=p(y), а за новую переменную принять у, то порядок данного ур-ия понизится на единицу. В этом случае производные y’”, y”,…, находят по правилу дифференцирования сложной ф-ии:
y”=p’(y)y’=p’(y)p,
y”’=p”(y)y’p+p’(y)p’(y)y’=p”(y)p2(p’(y))2p
Простейшее из таких ур-ий имеет вид:
F(y, y’, y”)=0 или y”=f(y,y’).
С помощью подстановки y’=p(y) его сводят к ур-ию p*p’(y)=f(y,p), с неизвестной функцией р, затем из ур-ия y’=p(y) находят у.
Пример 18.3 Найти общее решение или общий интеграл ур-ия yy”+(y’)2=0
Решение.
Это ур-ие вида F(y,
y’,
y”)=0.
Положим y’=p(y).
Тогда y”=p’(y)y’=p’(y)p
и данное ур-ие примет вид ypy’(y)+p2=0
или p(y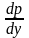 +p)=0.
Пусть р≠0. Тогда у
+р=0,
ydp+ydy=0.
Разделив ур-ие на р*у и проинтегрировав
его, получим:
+p)=0.
Пусть р≠0. Тогда у
+р=0,
ydp+ydy=0.
Разделив ур-ие на р*у и проинтегрировав
его, получим:
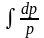 =
-
=
-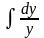 ,
ln
,
ln
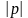 =
-ln
=
-ln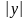 + ln
+ ln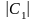 ,
p=
,
p=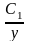 .
.
Подставив
в последнее ур-ие p=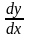 ,
получим ур-ие
=
,
ydy=C1dx.
После его интегрирования имеем:
,
получим ур-ие
=
,
ydy=C1dx.
После его интегрирования имеем:
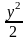 =
С1х+С2,
у2=2(С1х+С2).
=
С1х+С2,
у2=2(С1х+С2).
Т.о., получим общий интеграл исходного ур-ия.
21. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Определение 18.2 Уравнение вида
a n y n + a(n-1)y(n-1) + a(n-2)y(n-2) + … + a1y1 + a0y =0 (18.6)
где a i (i=0,n) - постоянные числа, называются линейным однородным ДУ n –го
порядка с постоянными коэффициентами.
Общее решение уравнения (18.6) имеет вид:
y = C1y1 + C2y2 + … + Cnyn, (18.7)
где Ci(i=1,n) произвольные постоянные, yi(i=1,n) частные решения уравнения (18.6).
Частные решения уравнения(18.6) ищут в виде: y = e kx.
Определяют коэффициенты k из характеристического уравнения:
ankn + a(n-1)k(n-1) + a(n-2)k(n-2) + … + a1k + a0 =0 (18.8)
При решении уравнения (18.8) возможны следующие случаи:
1) Все корни характеристического уравнения (18.8) действительны и различны. Тогда каждому ki соответствует частное решение вида:
yi = e^(kix) , i=1,n
Эти частные решения являются линейно независимыми и общее решение уравнения (18.6) имеет вид:
y = C1e^(k1x) + C2e^(k2x) + … + Cne^(knx).
2) Все корни действительны и среди них имеются равные.
В этом случае каждому действительному корню k кратности r соответствует r линейно независимых частных решений
ekx , xekx , x2ekx, … , x(r-1)ekx .
Если характеристическое уравнение (18.8) имеет корни k1 = k2 = … = kr = k, k(r+1), … , kn; то общее решение уравнения (18.6) запишется в виде:
y = ekx(C1 + C2x + … +Crx(r-1)) + C(r+1)e^(k(r+1)x) + … + Cne^(knx)
3)
Среди корней характеристического
уравнения имеются комплексные. Тогда
каждой паре комплексных корней k1
=
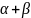 I
, k2
=
I
, k2
=
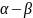 I
кратности
m
соответствует m
пар линейно независимых частных решений
вида:
I
кратности
m
соответствует m
пар линейно независимых частных решений
вида:
e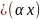 cos
cos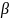 x,
xe
cos
x,
… , x
x,
xe
cos
x,
… , x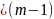 e
cos
x;
e
cos
x;
e
sin
x,
xe
sin
x,
… , x
e^(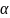 x)
sin
x.
x)
sin
x.
Т.е. каждой паре комплексных сопряженных корней k1 = I , k2 = I соответствует в общем решении уравнения (18.6) слагаемое вида
e^(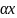 )
(C1cos
x
+ C2sin
x).
)
(C1cos
x
+ C2sin
x).
