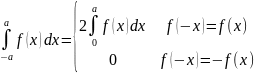- •1. Понятие о первообразной и неопределенном интеграле.
- •2. Основные свойства неопределенного интеграла.
- •3. Основные методы интегрирования. Метод замены переменной интегрирования.
- •4. Основные методы интегрирования. Интегрирование по частям.
- •5. Интегрирование простейших иррациональностей.
- •6. Понятие определенного интеграла.
- •7. Геометрический смысл определенного интеграла.
- •8. Основные свойства определенного интеграла.
- •9. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •11. Несобственные интегралы с бесконечными пределами интегрирования. Несобственные интегралы с бесконечными пределами интегрирования
- •22. Решение линейного неоднородного дифференциального уравнения методом вариации произвольных постоянных.
- •28. Понятие знакочередующегося ряда. Теорема Лейбница.
- •31. Классическое определение вероятности.
- •32. Свойства вероятности.
- •33. Понятие относительной частоты. Статистическая вероятность.
- •34. Геометрические вероятности.
- •35. Основные формулы комбинаторики.
- •36. Теоремы сложения вероятностей.
- •37. Теоремы умножения вероятностей.
- •38. Формула полной вероятности.
- •39. Вероятность гипотез. Формулы Бейеса.
- •40. Повторение испытаний. Формула Бернулли.
- •41. Повторение испытаний. Локальная теорема Лапласа.
- •42. Повторение испытаний. Интегральная теорема Лапласа.
- •45. График функции распределения.
- •46. Плотность распределения вероятностей нсв. Свойства плотности распределения.
- •47. Нахождение функции распределения по известной плотности распределения.
- •48. Математическое ожидание дсв.
- •49. Свойства математического ожидания. Математическое ожидание числа появлений события в независимых испытаниях.
- •50. Дисперсия дискретной случайной величины.
- •51. Свойства дисперсии. Дисперсия числа появлений события в независимых испытаниях.
- •52. Числовые характеристики непрерывных случайных величин.
- •53. Понятие о теоретических моментах распределения.
- •Влияние параметров нормального распределения на форму нормальной кривой.
- •81. Статистическая проверка параметрических гипотез. Ошибки первого и второго рода. П.2. Ошибки первого и второго рода.
- •Проверка гипотез равенства математических ожиданий двух случайных величин (большие независимые выборки).
- •89. Геометрическая интерпретация и графическое решение злп.
- •90. Понятие симплексного метода.
- •91. Понятие двойственности. Построение пары взаимно двойственных
- •92. Первая теорема двойственности и ее экономическое содержание.
- •93. Вторая теорема двойственности и ее экономическое содержание.
- •1. Понятие о первообразной и неопределенном интеграле.
- •2. Основные свойства неопределенного интеграла.
- •3. Основные методы интегрирования. Метод замены переменной интегрирования.
5. Интегрирование простейших иррациональностей.
1)Интеграл
вида
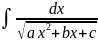 приводится к табличным интегралам вида
приводится к табличным интегралам вида
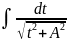 (если a
(если a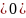 или
или
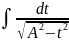 (если a
(если a
2)В
интеграле вида
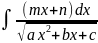 (m
(m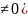 из числителя выделяется производная
2ax+b.
В результате приходим к табличным
интегралам и интегралам первого вида.
из числителя выделяется производная
2ax+b.
В результате приходим к табличным
интегралам и интегралам первого вида.
3)Интегралы
вида
 (m
с помощью подстановки
(m
с помощью подстановки
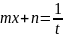 приводится к видам рассмотреным ранее.
приводится к видам рассмотреным ранее.
4)Интегралы
вида
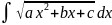 путем выдиления полного квадрата
приводится к одному из трех видов:
путем выдиления полного квадрата
приводится к одному из трех видов:
1)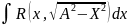
2)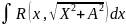
3)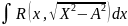
Интегралы
этих трех видов тригинометрическими
подстановками сводятся к интегралам
функций рационально зависящих от
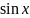 и
и
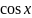 .
Для этого достаточно в интегралах вида
(1) применить подстановку
.
Для этого достаточно в интегралах вида
(1) применить подстановку
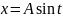 или
или
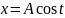 ,
в интегралах вида (2) – подстановку
,
в интегралах вида (2) – подстановку
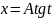 или
или
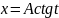 ,
в интегралах вида (3) – подстановку
,
в интегралах вида (3) – подстановку
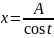 или
или
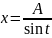
6. Понятие определенного интеграла.
П усть
функция f(x)
определена на отрезке
усть
функция f(x)
определена на отрезке
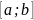 .
Разобьем
произвольно этот отрезок на n
частей точками
.
Разобьем
произвольно этот отрезок на n
частей точками
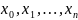 где
где
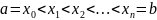 .
.
Обозначим
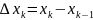 , и пусть
, и пусть
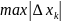 - длинна наибольшего из отрезков разбиения
(ее называют диаметром
разбиения).
На каждом отрезке
- длинна наибольшего из отрезков разбиения
(ее называют диаметром
разбиения).
На каждом отрезке
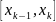 произвольно выберем точку
произвольно выберем точку
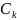 и составим сумму
и составим сумму
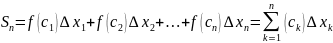 ,
которую называют интегральной
суммой Римана функции
f(x),
соответствующей данному разбиению
отрезка
и выбору точек
,
которую называют интегральной
суммой Римана функции
f(x),
соответствующей данному разбиению
отрезка
и выбору точек
 .
.
Рассмотрим
предел интегральных сумм при стремлении
диаметра разбиения к нулю, т.е.
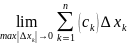 .
.
Если
существует конечный предел последовательности
интегральных сумм
 при условии, что наибольшая из разностей
при условии, что наибольшая из разностей
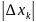 ,
стремится к нулю, причем этот предел не
зависит от способа разбиения отрезка
и от выбора точек
,
то функцию f(x)
называют интегрируемой
по Риману на
отрезке
,
а сам предел называют определенным
интегралом от
функции f(x)
в пределах от a
до b
и обозначают символом
,
стремится к нулю, причем этот предел не
зависит от способа разбиения отрезка
и от выбора точек
,
то функцию f(x)
называют интегрируемой
по Риману на
отрезке
,
а сам предел называют определенным
интегралом от
функции f(x)
в пределах от a
до b
и обозначают символом
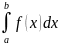 .
.
По
определению
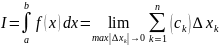 определенный интеграл от f(x)
на
,
есть некоторое число I
(его так же называют интегралом Римана
от f(x)
на
)
определенный интеграл от f(x)
на
,
есть некоторое число I
(его так же называют интегралом Римана
от f(x)
на
)
7. Геометрический смысл определенного интеграла.
П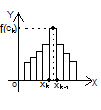 усть
f(x)
непрерывная на
функция, причем
усть
f(x)
непрерывная на
функция, причем
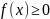 для
для
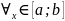 .
Криволинейной
трапецией называют
фигуру ограниченную графиком функции
f(x),
прямыми
.
Криволинейной
трапецией называют
фигуру ограниченную графиком функции
f(x),
прямыми
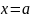 ,
,
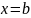 и осью
и осью
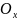 .
.
Произведение
f(x)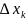 равно площади прямоугольника с основанием
и высотой f
равно площади прямоугольника с основанием
и высотой f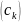 ,
а сумма представляет собой площадь
ступенчатой фигуры, изображенной на
рисунке.
,
а сумма представляет собой площадь
ступенчатой фигуры, изображенной на
рисунке.
Если
при стремлении к нулю диаметра разбиения
отрезка
существует предел, то естественно
величину I
называют площадью
криволинейной трапеции. Таким
образом с геометрической точки зрения
определенный
интеграл от неотрицательной функции
есть площади соответствующей криволинейной
трапеции:
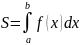 .
.
8. Основные свойства определенного интеграла.
1)Определенный
интеграл не зависит от обозначения
переменной интегрирования, т.е.
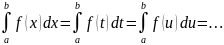
2)Постоянный
множитель можно выносить за знак
определенного интеграла, т.е.
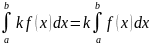 ,
где k-const.
,
где k-const.
3)Определенный
интеграл от алгебраической суммы функций
равен сумме их интегралов, т.е.
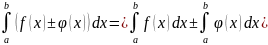
4)Имеет
место равенство:
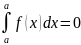 .
.
5)Для
любых чисел a,
b
и с справедливо равенство:
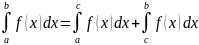 ,
если все три интеграла существуют.
,
если все три интеграла существуют.
6)При
перестановке пределов интегрирования
определенный интеграл меняет знак, т.е.
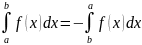 .
.
7)Если
на отрезке
функция f(x)
и
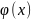 удовлетворяют условию f(x)
удовлетворяют условию f(x)
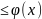 ,
то
,
то
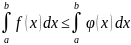 .
.
8)Если
подынтегральная функция на отрезке
интегрирования не меняет знак, то
интеграл представляет собой число того
же знака, что и функция, т.е.
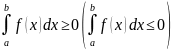 при f(x)
при f(x)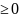 (f(x)
(f(x)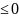 )
для
.
)
для
.
9)(Теорема
об оценке) Если M
и m
– наибольшее и наименьшее значения
f(x)
на отрезке
,
то
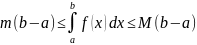 .
.
10)(Теорема
о среднем) Если f(x)
непрерывна на
,
то существует такая
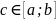 ,
что
,
что
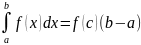 .
.
11)Интегрирование
в симметричных пределах можно упростить
по формулам: