40. Повторение испытаний. Формула Бернулли.

Определение _20.8: Если производится несколько испытаний причём вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

Определение _20.9: Сложным называют событие которое совмещает несколько отдельных ( простых ) событий.

Пусть производится n независимых испытаний в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же и равна p. Следовательно вероятность не наступления события А в каждом испытании также постоянна и равна:

q = 1 – p

Поставим задачу вычислить вероятность того, что при n испытаниях событие А осуществится ровно k раз и следовательно не осуществится n – k раз при этом не требуется чтобы событие повторялось k раз в определённой последовательности.

Например, если речь идёт о появлении события А 3 раза в 4 испытаниях, то возможны следующие варианты :

, , ,

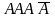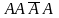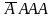
Вычислить искомую вероятность, которую обозначим 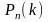можно по формуле Бернул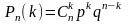ли :

или

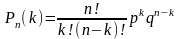
Пример _20.12 : Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной, равна p = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течении 4 суток не превысит нормы.

Решение : Вероятность нормального расхода электроэнергии в продолжении каждых из 6 суток постоянна и равна 0,75 суток.

Следовательно вероятность перерасхода электроэнергии каждые сутки также постоянна и равна :

q = 1 – p = 1 – 0,75 = 0,25

Искомая вероятность по формуле Бернулли равна :

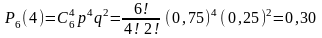
41. Повторение испытаний. Локальная теорема Лапласа.

Так как при больших значениях n пользоваться формулой Бернулли достаточно трудно, то естественно возникает вопрос о существовании иной формулы.

Теорема _20.8 : ( локальная теорема Лапласа ) Если вероятность p появление в событии А в каждом испытании постоянно и отлично от 0 и 1, то вероятность того, что событие А появится в n испытаниях равна k раз, приближённо равна ( тем точнее, чем больше n ) значению функции

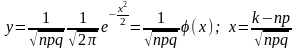
Имеются таблицы в которых помещены значения функции 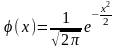, соответствующие значениям аргумента x

Для отрицательных значений аргумента пользуются теми же таблицами, так как функция 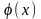чётная, т. е. .

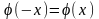Таким образом вероятность того что событие А появится в n независимых испытаниях равна k раз приближённо равна :

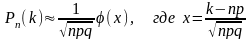
42. Повторение испытаний. Интегральная теорема Лапласа.

Предположим, что производится n испытаний в каждом из которых вероятность появления события А постоянна и равна p ( 0 < p < 1). Вычислим вероятность 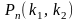того, что событие А появится в n испытаниях не менее k₁ и не более k₂ раз.

Теорема _20.9: (интегральная теорема Лапласа) Если вероятность p наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность 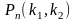того, что событие А появится в n испытаний от k₁ до k₂ раз приближённо равна определённому интегралу :

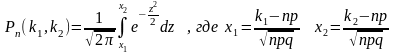
При решении задач, приближающих использования интегральной теоремы Лапласа пользуются таблицами, т. к. неопределенный интеграл 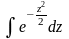не выражается через элементарные функции.

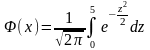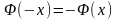Таблица содержит значение функции для положительных значений от 0 до 5 и для x=0 и x<0 пользуются той же таблицей учитывая что функция нечётная, т. е. . Для значений x>5 функции придаётся значение 0,5.

На практике применяют формулу имеющую вид :

Таким образом вероятность того, что событие А появится n независимых испытаний от k₁ до k₂ раз :

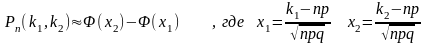
43. Понятие случайной величины. Закон распределения вероятностей ДСВ. П.1Понятие СВ. СВ наз. величину, которая в результате испытания примет одно и только одно возможное значение, первоначально неизвестное и завис от случайных причин, которые заранее не могут быть уточнены.

Дискретной (прерывной) наз СВ, которая принимает отдельные возможные значения с определенными вероятностями. Число возможных значений ДСВ м.б. конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.Число их значений бесконечно.

П.2 Закон распред-я вероятностей ДСВ

Законом распределения CВ наз соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями (его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения ДСВ первая строка таблицы содержит возможные значения, а вторая - их вероятности (Табл.1).

Таблица 1

Х х1 х2 ... х_n

p p1 p2 ... p_n

Сумма вероятностей второй строки таблицы 1, равна единице:

p1 + p2 + ...+ pn = 1.(события образуют полную группу). Если множество возможных значений Х бесконечно, то ряд p1 + p2 + ... сходится и его сумма =1.

Для наглядности з-н распределения ДСВ изображают графически, для чего впрямоугольной системе координат строят точки(х_і, р_і), а затем соедіняютих отрезками прямых

44. Функция распределения вероятностей случайной величины. Свойства функции распределения. в отличие от дискретной, непрерывная СВ не может быть задана перечнем всех её возможных значений и их вер-тей.

Возьмём СВ Х, возможные значения которой полностью заполняют интервал (а,в).Составить перечень всех возможных знач. Х нельзя , поэтом необх. Дать общий способ задания любых типов СВ . С этой целью и вводят ф-ции распределения вероятностей СВ.

Пусть х-действительное число. Вер-ть соб., состоящего втом, что Х примет значение , меньше х (вер-ть соб. Х< x) обознач. через F(x). функция F(x) = Fx (x) = P(x < x) называется функцией распределения случайной величины x .Она определяет вер-ть того,что СВХ в рез-те испытания примет значение меньше Х. Геометрически это рав-во можно опред-ть так: F(x) есть вер-ть того, что СВ примет значение , кот. Изображается на числовой оси точкой, дежащей левее точки х.

Свойства функции распределения

1)значения функции распределения принадлежат отрезку [0, 1].

2)F(x2)≥ F(x1 ), если x2, > x1, т.е. функция распределения вероятностей является неубывающей функцией.

Следствие 1. Вероятность того, что случайная величина X примет значение, заключенное в интервале (α, β), равна приращению функции распределения на этом интервале, т.е.P (α ≤ Х <β) = F(β) – F(α). (9)

Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Р (Х = х1) = 0.

Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.

Заметим, что было бы неправильно думать, что рав-во Р(Х=х₁) означает что событие Х=х1 невозможно.

Действ-но в рез-те испытания СВ обязательно примет одно из возможных значений ровно как и значение х1.

3)Если возможные значения СВХ принадлеж интерв (а, в), то: F(x)=0 при х ≤а и F(x)=0 при в≤х

Следствие.Если возможные значения НСВ расположены на всей оси Ох то справедливо соотношение lim(x→-∞)F(x)=0 и lim(x→+∞)F(x)=1