Вторая формула для вычисления дисперсии:

Теорема: дисперсия равна разности между мат. ожиданием квадрата случайной величины и квадрата ее мат. ожидания.

D(X) = M(X²) — (M(X))²

Пример: найти дисперсию случайной величины, которая задана следующим законом распределения:

Х	2	3	5
Р	0,1	0,6	0,3

1. Высчитываем математическое ожидание:

М(Х) = 2 ∙ 0,1 + 3 ∙ 0,6 + 5 ∙ 0,3 = 0,2 + 1,8 + 1,5 = 3,5

2. Рисуем закон распределения КВАДРАТА случайной величины ( то есть все значения Х из данного нам в условии задачи закона распределения мы возводим в квадрат, а вероятности при этом НЕ МЕНЯЮТСЯ!)

Х	4	9	25
Р	0,1	0,6	0,3

13. Ищем математическое ожидание КВАДРАТА случайной величины:

M(X²) = 4 ∙ 0,1 + 6 ∙ 0,6 + 25 ∙ 0,3 = 0,4 + 5,4 + 7,5 = 13,3

4. По формуле высчитываем дисперсию:

D(X) = M(X²) — (M(X))² = 13,3 — (3,5)²= 1,05

24. Свойства дисперсии дискретной случайной величины.

1. Дисперсия постоянной величины равно нулю:

D(C)=0

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

D(CX)=C*C*D(X) - (нужно писать С в квадрате)

3. Дисперсия суммы двух независимых случайных величин равно сумме дисперсий этих случайных величин:

D (X+Y)=D(X)+D(Y)

Следствие. Дисперсия суммы нескольких взаимно независимых случайных величин равно сумме дисперсий этих величин.

4. Дисперсия разности двух независимых случайных величин равно сумме дисперсий этих случайных величин:

D(X-Y)=D(X)+D(Y)

28. Полигон частот. Принципы построения. Пример.

Для наглядности строят различные графики статистического распределения, например, полигон.

Полигоном частот называют ломаную, отрезки которой соединяют точки (х₁; n₁), (x₂;n₂), …, (x_k;n_k)

Для построения полигона частот на оси абсцисс откладывают варианты x_i; а на оси ординат — соответствующие им частоты n_i. Точки (x_i; n_i) соединяют отрезками прямых и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x₁; w₁), (x₂; w₂), …, (x_k; w_k)

Пример: учебные достижения учащихся некоторого класса по математике характеризуются данными, представленными в таблице:

Количество баллов х	1	2	3	4	5	6	7	8	9	10	11	12
Число учащихся n	1	1	2	3	4	4	6	5	3	3	2	1

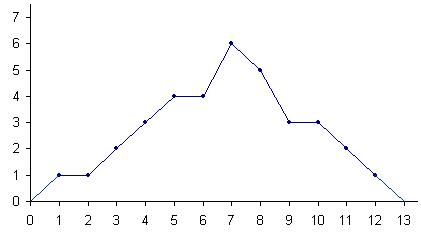
Построить полигон частот.

Решение.

Строим точки основываясь на данных из таблицы. Полученные точки соединяем отрезками прямой. Обратите внимание на точки (0; 0) и (13; 0), расположенные на оси абсцисс и имеющие своими абсциссами числа, на 1 меньшее и большее, чем соответственно абсциссы самой левой и самой правой точек. Полигон частот изображен на рисунке.