
12. Рассмотрим механизм возникновения и основные соотношения, характерные для синусоидальной ЭДС. Для этого удобно использовать простейшую модель — рамку, вращающуюся с постоянной угловой скоростью ω в равномерном магнитном поле (рис. 2.1, а). Проводники рамки, перемещаясь в магнитном поле, пересекают его, и в них на основании закона электромагнитной индукции наводится ЭДС. Значение ЭДС пропорционально магнитной индукции В, длине проводника l и скорости перемещения проводника относительно поля vt:
е = Blvt .
Выразив скорость vt через окружающую скорость v и угол α, получим
е = Blv sin α = Еm sin α.
Угол α равен произведению угловой скорости рамки ω на время t:
α = ωt..
Таким образом, ЭДС, возникающая в рамке, будет равна
е = Ет sin α = Em sin ωt.
|
Рис. 2.1. Модель, поясняющая возникновение синусоидальной ЭДС (а); графики мгновенных значений ЭДС (б) |
За один поворот рамки происходит полный цикл изменения ЭДС.
Если при t = 0 ЭДС е не равна нулю, то выражение ЭДС записывается в виде
е = Еm sin (ωt + ψ),
где е - мгновенное значение ЭДС (значение ЭДС в момент времени t); Ет — амплитудное значение ЭДС (значение ЭДС в момент времени ωt + ψ = π/2), (ωt + ψ) - фаза; ψ - начальная фаза. Фаза определяет значение ЭДС в момент времени t, начальная фаза — при t = 0.
Таким образом для получения синусоидального токанеобходимо:
Магнитное поле;
Движение проводника в поле;
Замкнутый контур.
13. Синусоидальный ток – переменный ток, изменяющийся во времени по синусоидальному закону.
Переменный ток – ток изменяющийся по величине и направлению во времени с определённой частотой.
Мгновенное значение синусоидального тока – значение в конкретный момент времени.

Где
Im – амплитудное значение тока – наибольшее значение тока за период.
 -
угловая частота
-
угловая частота
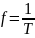 -
частота – число колебаний в единицу
времени
-
частота – число колебаний в единицу
времени
 -
период – время одного колебания.
-
период – время одного колебания.
 -
фаза, которая характеризует состояние
колебания в момент времени.
-
фаза, которая характеризует состояние
колебания в момент времени.
 -
начальная фаза.
-
начальная фаза.
Среднее значение синусоидального тока – среднее значение тока за полупериод.
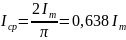
Действующее значение(среднеквадратичное) синусоидального тока – значение тока, при котором действие переменного тока(например тепловое) пропорционально квадрату данного значения.
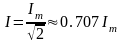 .
.
На это значение реагируют приборы электромагнитной, электродинамической и тепловой систем.
14. Закон Ома в комплексной форме.

 – вектор
тока(комплекс действующего значения
тока)
– вектор
тока(комплекс действующего значения
тока)
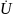 -
вектор
напряжения(комплекс действующего
значения напряжения)
-
вектор
напряжения(комплекс действующего
значения напряжения)
 -
комплекс
сопротивления
-
комплекс
сопротивления
Пример:
через зажимы двухполюсника с комплексным
сопротивлением
 протекает синусоидальный ток
протекает синусоидальный ток
 Определить напряжение u(t)
на зажимах.
Определить напряжение u(t)
на зажимах.
Решение:
 ;
;
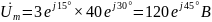
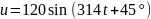
15. Законы Кирхгофа в комплексной форме.
Первый
закон Кирхгофа в символической форме: .
.
Второй
закон Кирхгофа в символической форме:
 .
.
Пример:
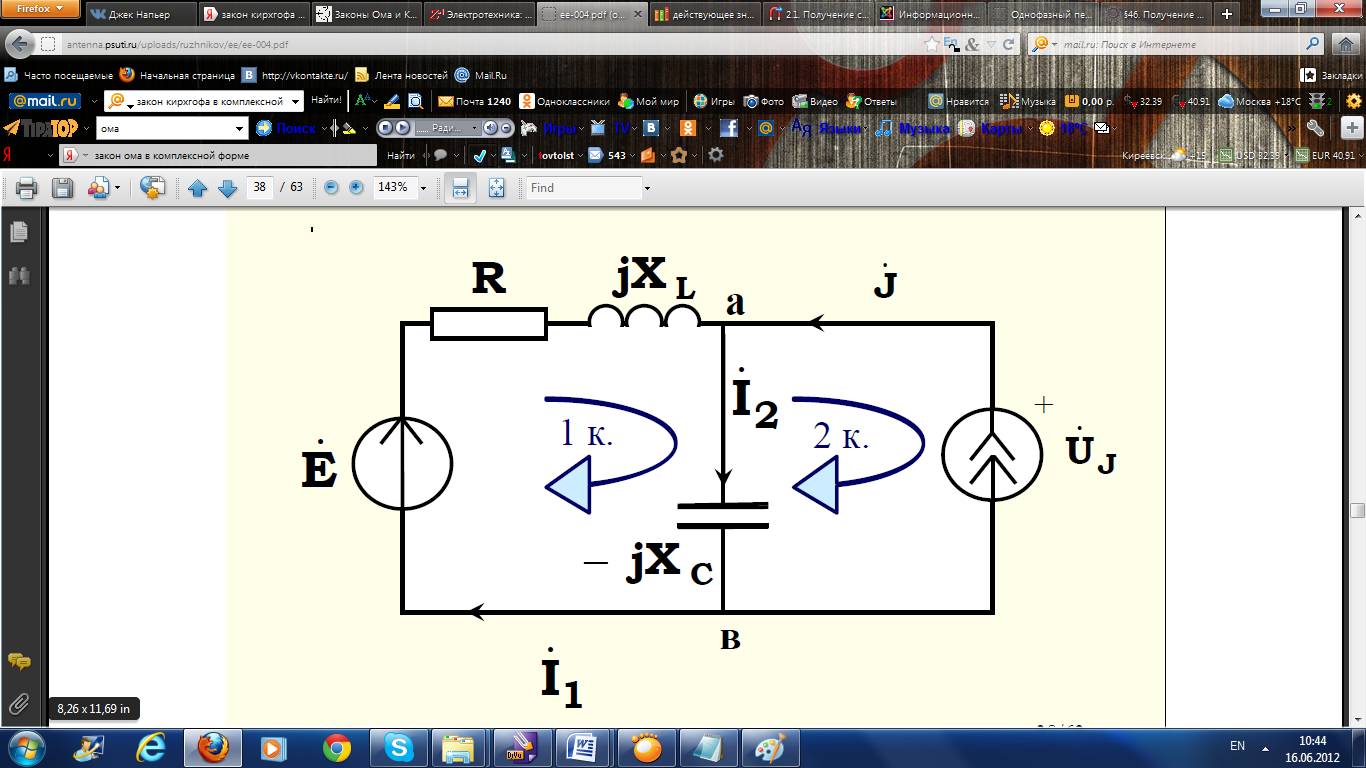
Nу=2, Nв=3,
N=Nв-NJ=3-1=2; N1=2-1=1; N2=2-1=1
a:

1:

16. Активное сопротивление(R) - величина, характеризующая сопротивление электрической цепи (или ее участка) электрическому току, обусловленное необратимыми превращениями электрической энергии в др. формы (преимущественно в тепловую).
Реактивное сопротивление(X) - электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).(мнимое сопротивление)
Индуктивное сопротивление (XL)– коэффициент пропорциональности между напряжением на выводах катушки, и током, протекающим через неё.
Ёмкостное сопротивление(XC) – коэффициент пропорциональности между напряжением на выводах конденсатора и током во внешней цепи конденсатора.
Полное сопротивление(Z) – совокупность активного и реактивного сопротивления, характеризующая все потери в цепи.
XL=ωL, где L – индуктивность, а ω – циклическая частота
XC=1/(ωC) , где С – емкость конденсатора
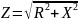
Комплекс полного сопротивления:

Можно вести расчёты, пользуясь треугольником сопротивления. Чертим отрезок, равный величине активного сопротивлении- это первый катет. Затем из конца его откладывается перпендикулярно – ХL вверх, XC вниз – реактивное сопротивление – второй катет. Соединяя свободные концы отрезка, получаем гипотенузу – модуль полного сопротивления. Угол между активным и полным сопротивлением показывает сдвиг фаз между током и напряжением.
Пример. Произвести расчет полного сопротивления переменного тока, в которую включена катушка, индуктивность которой L=0,096 Гн, с активным сопротивлением R=40 Ом. Напряжение на зажимах катушки 120 В. Посчитать модуль полного сопротивления по закону Ома, зная, что I=2,4 A.
ХL=314*0,096=30 Ом

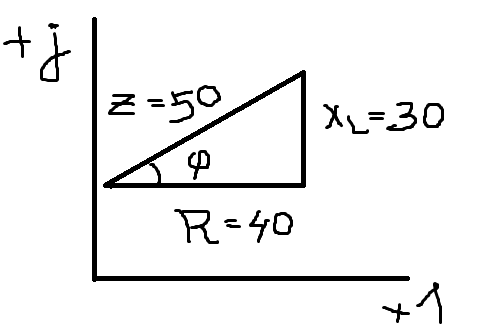
z=120/2,4=50 Ом
17. Для того, что бы построить вектор суммы нескольких векторов нужно из конца первого вектора построить второй, из конца второго третий и так далее, а затем соединить начало первого вектора с концом последнего.
Для того, что бы построить вектор разности двух векторов нужно соединить конец вычитаемого вектора с концом уменьшаемого вектора.
Диаграмма токов всегда строится по первому закону Кирхгофа, а диаграмма напряжений всегда строится по второму закону Кирхгофа.
Пример:
Д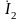 ано:
ано:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Требуется построить векторную диаграмму.
 ;
;
 ;
;
 ;
;

 ;
;
 ;
;
 ;
;
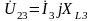 ;
;
 ;
;
18. Резонанс – явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям(резонансной частоте), определеляемым свойствами системы.
Резонанс в электрических цепях – такой режим работы цепи, включающий в себя индуктивные и емкостные элементы, при котором её входное сопротивление(проводимость) вещественно.
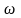
В цепи, в которой включены последовательно конденсатор, катушка индуктивности и конденсатор, возможно возникновение резонанса напряжений при определённых условиях.
Условия возникновения:
Цепь с источником переменного напряжения;
Последовательное включение реактивных элементов;
Равенство реактивных сопротивлений или равенство падений напряжения на реактивных элементах при условии, что C и L не равны 0.

Способы достижения:
Изменение L при постоянных С и ω;
Изменение С при постоянных L и ω;
Изменение ω при постоянных C и L.
И зменение
параметров цепи:
зменение
параметров цепи:
Нагрузка имеет чисто активный характер(z=R);
Отсутствует сдвиг фаз между напряжением и током;
Эквивалентная полная мощность цепи становится чисто активной(эквивалентная реактивная мощность равна 0)
Сила тока, протекающего в цепи в момент резонанса, будет максимальной
Падения напряжений на катушке и конденсаторе практически будут равны между собой
Идеальный резонанс напряжений эквивалентен короткому замыканию входных зажимов цепи
19. Резонанс – явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям(резонансной частоте), определеляемым свойствами системы.
Резонанс в электрических цепях – такой режим работы цепи, включающий в себя индуктивные и емкостные элементы, при котором её входное сопротивление(проводимость) вещественно.
П ри
параллельном соединении катушки
индуктивности и конденсатора возникает
резонанс
токов
при определённых условиях.
ри
параллельном соединении катушки
индуктивности и конденсатора возникает
резонанс
токов
при определённых условиях.
Условия возникновения:
Цепь с источником переменного напряжения;
Параллельное включение реактивных элементов;
Равенство реактивных проводимостей или равенство токов в параллельных ветвях при условии, что C и L не равны 0.

Способы достижения:
Изменение L при постоянных С и ω;
Изменение С при постоянных L и ω;
Изменение ω при постоянных C и L;
Изменение активного сопротивления в параллельных ветвях, при условии не равных 0 L и C и постоянной ω.

Изменение параметров цепи:
Сила тока на входе резонансного контура в момент резонанса будет минимальной
Токи, протекающие в параллельных ветвях практически равны между собой
Если считать катушку индуктивности идеальной (RК = 0), тогда токи в катушке и конденсаторе будут равны между собой
Идеальный резонанс токов эквивалентен разрыву (холостому ходу) в цепи
в режиме резонанса токов, вектор входного напряжения U совпадает по фазе с вектором входного тока IP = I, т.е. фазовый сдвиг между этими векторами:
Э = U - I = 0
Эквивалентная полная мощность цепи становится чисто активной(эквивалентная реактивная мощность равна 0)
20. Резонанс токов
Если
активные внутренние сопротивления
катушки индуктивности и конденсатора
не равны нулю, то
 ,
,
 .
.
Если
активное внутреннее сопротивление
конденсатора очень мало, то условие
резонанса токов примет следующий вид:
 .
.
Если
активные внутренние сопротивления
катушки и индуктивности и конденсатора
равны нулю, то условие резонанса примет
следующий вид:
 ,
откуда
,
откуда
 .
При этом
.
При этом
 .
.

Резонанс напряжений.
UL<UC UL=UC UL>UC
XL<XC XL=XC XL>XC

21.
Активная мощность
 [Вт]
- работа переменного тока за единицу
времени.
[Вт]
- работа переменного тока за единицу
времени.

Реактивная
мощность
 [ВAр]
- часть энергии, расходуемой на создание
электрических и магнитых полей в
реактивных элементах.
[ВAр]
- часть энергии, расходуемой на создание
электрических и магнитых полей в
реактивных элементах.

Полная
мощность
 [ВА]
- мощность, вырабатываемая источником
однофазного переменного ЭДС при cos
ф=1
[ВА]
- мощность, вырабатываемая источником
однофазного переменного ЭДС при cos
ф=1

φ=φu-φi – сдвиг фаз между током и напряжением, угол между полным и активным сопротивлением в треугольнике сопротивлений.
Cosφ – коэффициент мощности.
Связь
между активной, реактивной и полной
мощностью:
 .
.
Или S=P+jQ.
Расчётная формула для комплекса мощности:
 ,
где
I*=Ie-jφi
,
где
I*=Ie-jφi
Пример. Произвести расчет полного сопротивления переменного тока, в которую включена катушка, обладающая индуктивным сопротивлением ХL=30 Ом и активным сопротивлением R=40 Ом. Напряжение на зажимах катушки 120 В.

Cosφ=4/5 sinφ=3/5
I=120/50=2,4A
P=2,4*120*4/5=230,4 Вт
Q=2,4*120*3/5=172,8 Вар
S=120*2,4=288 ВА



22. Коэффициент мощности(cosφ) во многих электротехнических устройствах мал из-за силы магнитных полей, т.е. большой величины реактивной мощности и положительного угла сдвига фаз.
Результат: неполное использование генераторов, линий передач, увеличение потерь электрической энергии.
Выход: для увеличения cosφ необходимо включить параллельно приёмнику со значительной реактивной (индуктивной) составляющей тока батарею конденсаторов. Реактивный(емкостной) ток батареи конденсаторов IC компенсирует индуктивный ток приёмника.
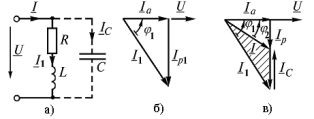
Если известен ток нагрузки I1 и коэффициент мощности приёмника cos φн и задано требуемое значение cos φ после компенсации, то необходимое значение ёмкости конденсатора можно определить при помощи векторной диаграммы токов, из которой следует:
Ia
tgφн
– Ia
tgφ=IC=ωCU,
откуда
 ,
где P=IaU
– активная мощность.
,
где P=IaU
– активная мощность.
Это искусственное улучшение. Естественное улучшение – полное использование мощности двигателей и установка синхронных двигателей с малым реактивным током.
Другие методы:
1) заменой мало загруженных двигателей двигателями меньшей мощности,
2) понижением напряжения
3) выключением двигателей и трансформаторов, работающих на холостом ходу
23. Активное сопротивление.
М
гновенное
значение тока имеет следующий вид:
 .
По закону Ома можно найти напряжение
на активном сопротивлении:
.
По закону Ома можно найти напряжение
на активном сопротивлении:
 ,
где
,
где
 - амплитудное напряжение. Комплекс
действующего значения тока:
- амплитудное напряжение. Комплекс
действующего значения тока:
 .
Комплекс действующего значения
напряжения:
.
Комплекс действующего значения
напряжения:
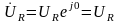 .
.
На активном сопротивлении, то есть на резисторе, ток и напряжение совпадают по фазе, или, другими словами, разность фаз между током и напряжением равна нулю.
М гновенная
мощность определяется по формуле:
гновенная
мощность определяется по формуле:
 .
Так как ток и напряжение совпадают по
фазе, то, очевидно, что мгновенная
мощность всегда будет иметь положительное
значение.
.
Так как ток и напряжение совпадают по
фазе, то, очевидно, что мгновенная
мощность всегда будет иметь положительное
значение.

Ёмкостное сопротивление – коэффициент пропорциональности между напряжением на выводах конденсатора и током во внешней цепи конденсатора. Назначение – предназначен для создания и усиления электрического поля, накопления заряда. Конструкция – два плоских проводника, находящихся на небольшом расстоянии друг от друга и разделённых диэлектриком. Принцип действия: при подключении конденсатора к источнику переменного тока происходит происходит поочерёдно процесс зарядки и разрядки конденсатора. При зарядке к одной обкладке, создавая объёмный отрицательный заряд, а от другой оттекают, создавая объёмный положительный заряд. Взаимодействие объёмных зарядов порождает электрическое поле, притяжение объёмных зарядов сохраняет этот поле, если отключить конденсатор от цепи. В цепях с конденсатором процесс создания объёмных зарядов инерционен, поэтому вектор напряжения отстаёт от вектора тока на 90 гр.
К омплексные
значения тока и напряжения будут иметь
следующий вид:
омплексные
значения тока и напряжения будут иметь
следующий вид:
 ;
;
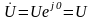 .
.
Ёмкостное
сопротивление
 .
.
Если
 ,
то
,
то
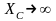 ,
то есть конденсатор можно заменить
разрывом цепи.
,
то есть конденсатор можно заменить
разрывом цепи.
Если
 ,
то
,
то
 ,
то есть конденсатор можно заменить
проводником.
,
то есть конденсатор можно заменить
проводником.

