Эксперименты / Зателепин. Баранов. Изменение температур при экранировании

Изменение температуры образца при экранировании свинцовой стенкой

Д.С. Баранов, В.Н. Зателепин

Лаборатория «ИНЛИС», Москва, bds07@yandex.ru, zvn07@yandex.ru

называть «ньютоний». Введено понятие «облучение ньютонием» атомарного вещества.

Введение

Предпосылкой для проведения этой работы стала необходимость протестировать работу термопары К-типа, подключенную к электронному регистратору температуры АТЕ-2036 компании АКТАКОМ, при измерении температуры воздуха, воды (с помощью, так называемого пробника, в котором термопара изолирована от внешней среды), порошка никеля, вольфрама и других сред. Мы используем эти термопары для измерения распределения температуры в устройстве, которое мы называем измеритель тепловой мощности, и которое подробно описано в нашей работе [1]. Одной из существенных особенностей этого устройства является наличие закрытого объема с

металлический ящик, аналогичный тому, что используется в установке по измерению тепловой мощности. Было обнаружено, что температура образцов, измеренная электронным термометром, зависит от того, находится ли образец внутри металлического ящика, или вне его. Кроме того, показания электронного термометра существенно зависят от множества других факторов, в частности от времени в течение суток.

Поиск в литературе показал, что эффект известен с 40-х годов прошлого века и называется «эксперимент Райха-Эйнштейна» [2]. На различие температур воздуха в металлическом ящике и вне его обратил внимание некто В.Райх, которому удалось заинтересовать А. Эйнштейна на проведение совместного эксперимента. По оценке А.Эйнштейна этот эффект может быть «бомбой» в физике Совместный эксперимент подтвердил, что действительно температура воздуха в устройстве, состоящем из вложенного в деревянный ящик металлического ящика, выше, чем температура воздуха вне устройства. А.Эйнштейн и его команда объяснили эффект тем, что в комнате существует естественная конвекция воздуха между полом и потолком, а

металлический ящик нарушает естественное распределение температуры. Т.е. «бомба» не состоялась. В.Райх не согласился с таким выводом. Он считал, что существует некая особая форма энергии, которая накапливается в устройстве. В дальнейшем он разработал для продажи в медицинских целях усложненную модификацию устройства, которое он назвал «Оргон аккумулятор». В статье [2] описываются эксперименты, в которых максимально демпфируется влияние естественной конвекции, но заметное различие температур в устройстве и вне его, тем не менее, остается.

Мы в своих экспериментах по тестированию термопар также наблюдаем заметную разницу температур воздуха в металлическом ящике и вне него. В 40-е годы прошлого века «холодный ядерный синтез» не был популярен в научных кругах, и поэтому искали более простые объяснения эффекту В.Райха. В наше время в первую очередь начали бы искать в металлическом ящике следы «холодного ядерного синтеза». Но мы попробуем дать иное, не менее интригующее объяснение этому эффекту.

Некоторые соображения по облучению «необычным веществом» атомарного вещества

поняли, что в этих очень простых на первый взгляд экспериментах мы совершенно упускаем нечто очень существенное для данного процесса. Мы предположили, что в этих экспериментах мы сталкиваемся с заметным проявлением так называемого «эфира». Собственно об этом писал В.Райх около 80-ти лет назад. Ведь введенная им «Оргон энергия», которая накапливается по его представлениям в металлическом ящике, по сути, является одной из многочисленных версий «эфира». Но в наших экспериментах мы заметили еще одну существенную особенность – температура в металлическом ящике заметно зависит от времени суток. Стало ясно, что если

Такая теория существует и называется «теория гравитации Ле Сажа». Как и водится в любой оригинальной теории, ее ввел совсем другой человек – Николя Фатио де Дюилье, швейцарский математик. Он в 1690 г. будучи молодым человеком 26 лет от роду предложил идею, объясняющую закон всемирного тяготения, который за 4 года до этого выдвинул И. Ньютон. Суть теории гравитации «Фатио - Ле Сажа» состоит в том, что нет центральной силы гравитации, которую ввел И.Ньютон, а есть силы

Сажа» объясняет и зависимость силы тяготения от расстояния (1/R2), и ее зависимость от массы тела. В теории «Фатио - Ле Сажа» есть существенные огрехи, на которые обращали внимание великие физики. Но, несмотря на недостатки, в теории «Фатио -

Ле Сажа» есть самое существенное – сила, которая нас придавливает к Земле, исходит не из Земли, как это предполагал И.Ньютон, а из космоса.

В настоящее время некоторые исследователи продолжают развивать теории гравитации на подобии теории «Фатио - Ле Сажа». Нам этот подход представляется плодотворным, но хочется высказать некоторые собственные соображения на этот счет. Можно предположить, что в космосе (т.е. вдалеке от звезд и планет) существует сравнительно изотропный поток «эфирного вещества». Этот поток облучает со всех сторон объекты, состоящие из атомарного вещества. Это облучение всех атомарных тел «эфирным веществом» в дальнейшем мы будем называть «эфирное облучение». Поток «эфирного вещества» в окрестности звезд и планет становится неизотропным, т.к. «эфирное вещество» при движении через планету или звезду упруго или неупруго взаимодействует с атомарным веществом. «Эфирный поток» пришедший на

облучает материальные тела на Земле из-за экранирования части «эфирного потока», двигающегося через Землю, – причина силы тяжести на Земле.

Оценим массу элементарной частицы «эфирного вещества». Такие оценки существуют в литературе. Например, в [3] на основе закона смещения Вина авторы приходят к выводу, что масса элементарной частицы эфира 5,6 *10-40 кг. Можно сделать эту оценку другим способом. Предположим, что электромагнитная волна - это «звуковые» волны в «эфирном веществе». Используя принятые в газовой динамике

где m – масса элементарной частицы эфира, к = 1,38 *10-23 постоянная Больцмана,

g = 4/3- отношение изоэнтропы для электромагнитного излучения, c2 = 8,99*1016 - квадрат скорости света. Примем, что Тэфира =2,73 – температура реликтового излучения. Предположение о природе электромагнитной волны как волны сжимаемости «эфирного вещества» порождает множество вопросов. Но для нас сейчас важно то, что эфирная частица имеет очень малую массу. При температуре реликтового излучения масса элементарной частицы «эфирного вещества» на 9 порядков меньше массы электрона.

В своей статье «Попытка химического понимания эфира», опубликованной в 1902 году, Д.И.Менделеев высказал предположение о существовании двух неизвестных к тому времени веществ, которые он назвал «ньютоний» и «короний». «Ньютоний» по Менделееву обладает очень малой массой. В дальнейшем в этой работе мы будем называть «эфирные частицы» термином «ньютоний».

Ниже в разделе «Экспериментальный стенд и результаты измерений» будет сделана оценка потока энергии «ньютония»» qнью, приходящего к Земле из космоса. Воспользуемся этим результатом заранее для оценки плотности «ньютония» nнью в космосе. Заметим, что скорость звука в сжимаемой среде близка к средней скорости движения частиц этого вещества. Таким образом, скорость движения частиц

облучение «ньютонием» путем замера изменений температуры образца при наличии рядом с образцом тяжелой массы, экранирующей образец от этого облучения.

Встает вопрос, чем такой подход лучше, чем измерение силы взаимодействия образца и экранирующей массы. Ведь ясно, что приближение тяжелой массы к объекту приведет к изменению потенциальной энергии объекта и нагреет его. Ведь тело, упавшее на землю, нагреется. Но это кратковременный нагрев. Через некоторое время температура упавшего на землю тела выровняется с температурой окружающего

всегда будет отличаться от температуры воздуха, имеющего меньшую плотность. Это превышение стационарной температуры, например свинцового образца, над температурой окружающего воздуха мы постоянно наблюдали в наших экспериментах. Например, в экспериментах, которые будут описаны ниже, в стационарном режиме температура образца из свинца (пластинка размером 20*10*2 мм) выше на 1-1,5о F

чувствительным методом, чем измерение силы взаимодействия с этим телом. Несколько ниже в этом разделе мы прокомментируем это соображение.

Мы предположили, что на показания термометров в ящике оказывает влияние не то обстоятельство, что это замкнутый объем, а наличие у ящика стенок, которые в

Земле облучения «ньютонием», и (2), где образец экранируется от потока «ньютония» расположенным рядом тяжелым телом. Мы предположили, что поскольку одно из проявлений облучения «ньютонием» - сила тяжести, то свинец будет экранировать более эффективно, чем сталь, т.к. его плотность выше. Поэтому на стенде для экранирования термопары от облучения «ньютонием» используются свинцовые блоки размером 5*10*10 см, имеющие торцы специальной формы, позволяющие собирать из

В терминах уравнения (3) эксперимент состоит в изменении коэффициента b при экранировании образца. Из (3), предполагая, что при изменении коэффициента b, изменяется только Tобразца можно получить

Выражение (4) справедливо для квазистационарного режима, когда коэффициент b меняется с характерным временем много большим, чем характерное время установления стационарного режима для образца. Если экранировать поток «ньютония», падающий

называемым линейным коэффициентом ослабления, который зависит от массы вещества и длины пробега частицы «ньютония» в веществе. Если предположить, что плотность Земли по порядку величины совпадает с плотностью экранирующего вещества (свинец), то b пропорционален отношению толщины слоя экранирующего вещества к диаметру Земли. Это первые два члена разложения экспоненциальной зависимости. Из (4) видно, что при росте b (увеличении экранирования потока «ньютония») Tобразца будет уменьшаться.

Как было отмечено выше, измерение температуры при экранировании тяжелой массой является более чувствительным методом для обнаружения потока «ньютония» по сравнению с измерением силы тяжести. Дело в том, что стационарное решение для

(3) - равенство нулю потоков энергии в образец. И малейшие изменения коэффициента b в (3) приведут к заметному изменению суммарного потока в образец, и к измеряемому изменению температуры образца. А при попытке измерять изменение веса тела при экранировании, приходится фиксировать очень малые изменения веса на фоне большого значения величины веса тела. Для того, чтобы взвешивание тела было очень чувствительным методом, необходимо обнулить вес тела. На Земле это невозможно. А вот в космической станции вес тела компенсирован. Там замер изменения импульса тела при экранировании потока «ньютония» можно провести с гораздо большей точностью. Но конечно при проведении такого эксперимента всегда можно сказать, что это экран притягивает к себе космонавта, а не уменьшение потока «ньютония». Но при экранировании произойдет изменение стационарной температуры тела. А вот этот процесс объяснить силой тяготения не удастся. В следующем разделе мы приведем результаты экспериментов, которые показывают, что температура образца при экранировании меняется.

Экспериментальный стенд и результаты экспериментов

На фотографии (Рис. 1) виден объем, экранированный свинцовыми пластинами сверху. В данной работе представлен два типа экспериментов: эксперимент 1 - свинцовая стенка расположена над образцом, (2) – свинцовая стенка расположена сбоку от образца. Виден образец (свинцовая пластинка) с прикрепленной желтой клейкой лентой термопарой, расположенный внутри экранированного объема.

регистрирует и записывает показания термопар. Стенд размещен в закрытой темной внутренней комнате лаборатории, чтобы минимизировать изменение температуры воздуха в окрестности стенда в течение суток.

Эксперимент был разбит на три фазы и проводился следующим образом. Длительность каждой фазы эксперимента – 6 - 15 минут. Т.е. весь эксперимент длится

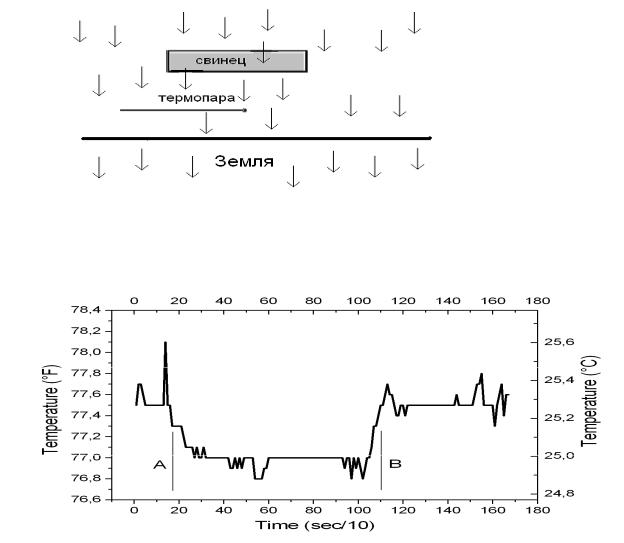
Рис.2 Схема эксперимента 1 в фазе 2.

Рис. 3 Зависимость показаний термопары в эксперименте 1 (экранирующая масса располагается сверху) от времени.

На Рис.3 фаза 1 (термопара находится в стороне от экранированной зоны) продолжалась до замера, отмеченного линией А на рисунке. В фазе 1 температура была примерно 77,5оF. Это состояние образца является квазистацинарным, т.к. образец находился в нем около 20 минут. В момент, отмеченный линией А на рисунке, образец

экранирован свинцовыми блоками. Видно, что температура, которую показывает термопара в это время снизилась на 0,5о F до значения 77,0о F. После момента, отмеченного линией В на рисунке, образец был вынесен из экранированного объема, и температура практически вернулась к значению, которое она показывала в начале эксперимента 1 77,5о F.

Применяя формулу (4) к данным Рис. 4 можно оценить мощность потока энергии, связанного с потоком «ньютония». Примем для dT в формуле (4) величину

поглощения потока «ньютония» в веществе, составляющем тело Земли, является объемным, в отличие от поглощения солнечного света, т.к. проникающая способность

энергия потока «ньютония», падающего на Солнце является мощным дополнительным к термоядерной энергии источником энергии, излучаемой Солнцем. Т.е. в теле вещества Солнца идет не только термоядерная реакция, но и преобразование кинетической энергии потока «ньютония» в тепловую энергию.

Также возможно, что при таком взаимодействии частицы «ньютония» передают атомарному веществу не только импульс, но и момент импульса. Именно это является

амплитудой осцилляций порядка 0,1 оF образец был помещен в зону около свинцовой стенки закрытой теплоизолятором

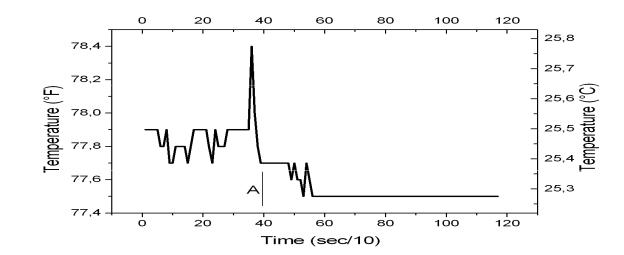
Рис. 4 Зависимость показаний термопары в эксперименте 2 от времени.

До линии «А» термопара находится вне экранированного объема. После линии «А» термопара была в экранированном объеме, который создан размещением свинцовых блоков сбоку. Видно, что температура после переноса термопары в зону экранирования начинает снижаться и через примерно 200 сек (20 замеров) достигает

стационара. Интересно то, что температура в зоне экранирования не флуктуирует. Также как и в эксперименте с расположением экрана над образцом можно сделать вывод, что экранирование снижает температуру образца.

Помещение образца с термопарой и слева, и справа от экрана приводит к снижению его температуры. При помещении образца над экраном температура меняется незначительно. А при помещении образца под экран (как мы видим на Рис.3) температура снижается на 0,5оF. Это подтверждает сделанное при получении оценки мощности потока «ньютония» предположение, что, проходя через Землю, поток «ньютония» практически полностью поглощается.

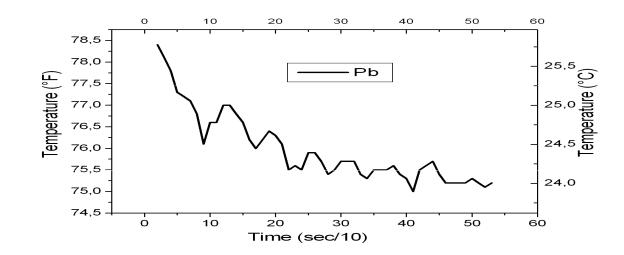
Рис. 5 Флуктуации температуры при расположении термопары под вращающейся свинцовой полосой.

На Рис.5 показаны результаты измерения температуры с помощью термопары расположенной в воздухе без свинцового образца. Над этой термопарой с помощью низкооборотного мотора вращалась свинцовая полоса, которая периодически то экранировала, то открывала облучение «ньютонием» термопары потоком, направленным к Земле. Наблюдаются общее снижение температуры, регистрируемое термопарой, и заметные периодические пульсации температуры.

Контрольные эксперименты

Термопара и регистрирующее устройство АТЕ-2036 являются электронными устройствами. Всегда остается вопрос о наведенных электромагнитных полях при расположении неподалеку свинцовой стенки, и влиянии этих полей на измерения. Поэтому были предприняты контрольные измерения изменений температуры образца

экраном. После удаления свинцового экрана показания термометра возвращались к