17.Целочисленное программирование.
Рассмотрим
ЗЛП: Z=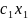
+…+
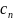
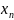→max(min)
(1)
+…+
=
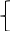
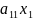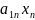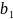
… …. …. (2)
+…+
=
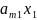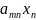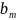
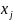≥0,
∀ j
∈ Z, ∀ j
Задача (1)-(2) - задача целочисленного линейного программирования
Задачи целочисл.линейн.программ. рассматр-ют тогда, когда речь идёт о произв-ве неделимой продукции. В этом случ. , если она решается симплекс-мет. и оптим-й план имеет целые коорд-ты, то задача решена. Если же хотя бы одна из коорд-т в опт-ном плане не целая, то отсекают от многогранника решений эту условную точку таким обр., чтобы все точки с целочисл. коорд-ми остались в многограннике.
Пусть x ∈R, тогда целой частью числа х – [x] – наз-ся наибольшее число, его не превосходящее . Дробн. часть числа x – {x}=x-[x]
18.Метод Гомари
1.Решают задачу симплекс-методом. Если все коорд-ты в оптим. плане целочисленные, то задача решена. Если нет, то переходим на п.2.
2.Выбираем в опт. плане коорд-ту с наибольш. дробн. частью. Записываем нерав-во
{
}
+…+{
}
≥{
}
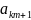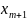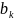и добавляем его в сис-му огранич.
+…+
=
… …. ….
+…+ =
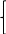≥0, ∀ j
∈ Z, ∀ j
3.Переходим
от неравенства к ур-ю:- {
}
- … - {
}
+
= -{
}
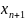и полученную задачу решаем
двойст.симп.-методом. Если опт. план
целочисленный, то задача решена. Если
нет, то переходим на п.2.
19.Транспортная задача(мат.Модель,определения)
Постановка задачи:некоторый однородный продукт содержится у m поставщиков А1,А2,…,Аm в кол-ве a1,a2,…,am единиц. Его необходимо доставить n потребителям B1,B2,…Bn, потребности которых сост-ют b1,b2,…,bn единиц.
Математич.модель:Пусть
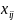– кол-во единиц груза, перевозимое от
i-того
поставщика к j-тому
потребителю. Соберём данные в таблицу:
b1 b2 … bn
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1
a2
.
.
.
am
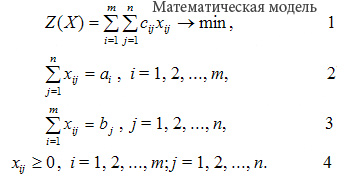\ЭЭ
Э
Это закрытая модель тр. задачи, т.к.
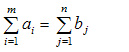. Если же ≠,то модель открытая.
Открытая модель сводится к закрытой.
Цикл – это последовательность клеток в матрице планирования, для которых 2 и только 2 соседние клетки в послед-ти располагаются в одной строке или одном столбце таблицы, а последняя клетка расп-ся в той же строке или столбце ,что и 1-ая. План перевозок будет попрным, если он ацикличный.
20.Транспортная задача(постр.Первонач.Опорн.Плана)
1.Выбираем
клетку, имеющую минимальн. стоим-ть.
Если min(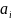
,
)=
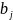,то вычёркиваем все остальные клетки
i-той
строки. Если же min(
,
)=
, то вычёрк. все остальн. клетки j-того
столбца. Если
=
тогда прочерки ставят или в i-той
строке или в j-том
столбце, но не одновременно.
2.Просматриваем невычеркнутые клетки, и среди них выбираем кл-ку с min стоим-тью. И повторяем процедуру пункта 1.
В рез-те получится n+m-1 занятая кл-ка и план ацикличный.