
- •1.Система координат
- •4.Уравнение прямой, проходящей через две заданные точки
- •5. Нормальное уравнение прямой
- •6.Расстояние от точки до прямой
- •7.Векторы
- •8.Общее уравнение плоскости в r3
- •10.Эллипс
- •11. Гипербола
- •Уравнения
- •Свойства
- •13.«Недекартовые» системы координат в пространстве
- •Полярные координаты
- •14.Сферическая система координат
- •15.Линейное пространство
- •Линейное векторное пространство. Линейное пространство векторов.
- •16.Линейная независимость
- •Определение
- •Свойства
- •Значение
- •17.Базис
- •Происхождение термина
- •Элементарное введение: базис в евклидовой плоскости и пространстве
- •Обозначения
- •Евклидово пространство
- •18.Ортогональность векторов. Перпендикулярность векторов.
- •19.Разложение вектора по базису
Обозначения
Обозначение векторов базиса может быть в принципе произвольным. Часто используют какую-нибудь букву с индексом (числовым или совпадающим с названием координатной оси), например:
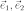
или

— типичные обозначения базиса двумерного пространства (плоскости).
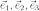
или
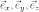
— трехмерного пространства. Для трехмерного пространства часто по традиции используется и обозначение

Представление какого-то конкретного (любого) вектора пространства в виде линейной комбинации векторов базиса (суммы базисных векторов числовыми коэффициентами), например
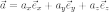
или
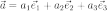
или,
употребляя знак суммы
 :
:

называется разложением этого вектора по этому базису.
Числовые
коэффициенты
 называются
коэффициентами разложения, а их набор
в целом — представлением (или
представителем) вектора
в
базисе
называются
коэффициентами разложения, а их набор
в целом — представлением (или
представителем) вектора
в
базисе
 (Разложение
вектора по конкретному базису единственно;
разложение одного и того же вектора по
разным базисам — разное, то есть
получается разный набор конкретных
чисел, однако в результате при
суммировании — как показано выше —
дают один и тот же вектор).
(Разложение
вектора по конкретному базису единственно;
разложение одного и того же вектора по
разным базисам — разное, то есть
получается разный набор конкретных
чисел, однако в результате при
суммировании — как показано выше —
дают один и тот же вектор).
Угол между векторами. Угол между вектором и осью.
Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.


рис.1.
Обозначение.
 .
Из определения
следует, что
.
Из определения
следует, что
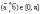 .
.
Мы полагаем очевидным, что при параллельном переносе любого из двух векторов угол между ними остается неизменным, только в этом случае поворот одного из векторов осуществляется либо в общей для обоих векторов плоскости, либо в плоскости параллельной другому вектору.
Евклидово пространство
Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.
В
современном понимании, в более общем
смысле, может обозначать один из сходных
и тесно связанных объектов, определённых
ниже. Обычно
-мерное
евклидово пространство обозначается
 ,
хотя часто используется не вполне
приемлемое обозначение
,
хотя часто используется не вполне
приемлемое обозначение
 .
.
1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:
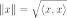 ,
,
в простейшем случае (евклидова норма):
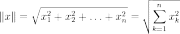
где
 (в
евклидовом пространстве всегда можно
выбрать базис,
в котором верен именно этот простейший
вариант).
(в
евклидовом пространстве всегда можно
выбрать базис,
в котором верен именно этот простейший
вариант).
2. Метрическое пространство, соответствующее пространству описанному выше. То есть с метрикой, введённой по формуле:
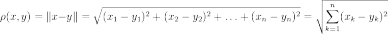 ,
,
где
и
 .
.
18.Ортогональность векторов. Перпендикулярность векторов.
Условие коллинеарности (параллельности или совпадения) векторов
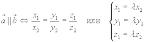
Условие ортогональности (взаимной перпендикулярности) векторов:

Условия ортогональности векторов. Два вектора A и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю
a· b= 0
19.Разложение вектора по базису
Определение 10.10 Множество векторов на прямой назовем одномерным векторным пространством, множество векторов на плоскости -- двумерным векторным пространством, в пространстве -- трехмерным векторным пространством.
Легко проверить,
что если
 --
какое-то векторное пространство,
--
какое-то векторное пространство,
 ,
,
 --
число, то
--
число, то
 и
и
 .
.
Определение
10.11
Линейной комбинацией векторов
 с
коэффициентами
с
коэффициентами
 называется
вектор
называется
вектор
 .
.

Рис.10.10.Примеры линейных комбинаций
Векторы d,f,g
на рисунке 10.10 и
 являются
линейными комбинациями векторов a,b,c:
являются
линейными комбинациями векторов a,b,c:
 ,
,
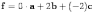 ,
,
 ,
,
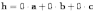 .
.
Будем говорить, что вектор b раскладывается по векторам , если b является линейной комбинацией этих векторов.
Предложение
10.1 Если
 ,
то любой вектор b,
коллинеарный a,
представим и причем единственным образом
в виде
,
то любой вектор b,
коллинеарный a,
представим и причем единственным образом
в виде
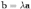 ,
где
,
где
 --
число.
--
число.
Доказательство.
В соответствии с определением
10.9 умножения вектора на число
 ,
если b
имеет направление, противоположное a,
и
,
если b
имеет направление, противоположное a,
и
 в
противном случае. Таким образом,
в
противном случае. Таким образом,
 или
или
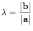 .
.
