- •1.Система координат
- •4.Уравнение прямой, проходящей через две заданные точки
- •5. Нормальное уравнение прямой
- •6.Расстояние от точки до прямой
- •7.Векторы
- •8.Общее уравнение плоскости в r3
- •10.Эллипс
- •11. Гипербола
- •Уравнения
- •Свойства
- •13.«Недекартовые» системы координат в пространстве
- •Полярные координаты
- •14.Сферическая система координат
- •15.Линейное пространство
- •Линейное векторное пространство. Линейное пространство векторов.
- •16.Линейная независимость
- •Определение
- •Свойства
- •Значение
- •17.Базис
- •Происхождение термина
- •Элементарное введение: базис в евклидовой плоскости и пространстве
- •Обозначения
- •Евклидово пространство
- •18.Ортогональность векторов. Перпендикулярность векторов.
- •19.Разложение вектора по базису
10.Эллипс

Эллипс, его фокусы и главные оси
Э́ллипс
(др.-греч.
ἔλλειψις — опущение, недостаток, в
смысле недостатка эксцентриситета
до 1) — геометрическое
место точек
M
Евклидовой
плоскости,
для которых сумма расстояний до двух
данных точек
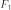 и
и
 (называемых
фокусами)
постоянна и больше расстояния между
фокусами, то есть
(называемых
фокусами)
постоянна и больше расстояния между
фокусами, то есть
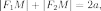 причем
причем

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.
Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.
11. Гипербола
Гипе́рбола (др.-греч.
ὑπερβολή, от др.-греч.
βαλειν — «бросать», ὑπερ —
«сверх») — геометрическое
место точек
M
Евклидовой
плоскости,
для которых абсолютное значение разности
расстояний от M
до двух выделенных точек
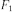 и
и
 (называемых
фокусами)
постоянно. Точнее,
(называемых
фокусами)
постоянно. Точнее,
 причем
причем

Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.
Кривая постоянной суммы расстояний между двумя точками — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини.
У этого термина существуют и другие значения, см. Парабола (значения).
Парабола, её фокус и директриса |
|
|
|
Коническое сечение: |
|
Эксцентриситет: |
|
Уравнение: |
|
гипербола · парабола · эллипс · окружность |
|
Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.
Уравнения
Каноническое уравнение параболы в прямоугольной системе координат:
 (или
(или
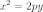 ,
если поменять местами оси).
,
если поменять местами оси).
Число
p называется фокальным параметром, оно
равно расстоянию от фокуса до директрисы[1].
Поскольку каждая точка параболы
равноудалена от фокуса и директрисы,
то и вершина — тоже, поэтому она лежит
между фокусом и директрисой на расстоянии
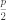 от
обоих.
от
обоих.
Квадратное
уравнение
 при
при
 также
представляет собой параболу и графически
изображается той же параболой, что и
также
представляет собой параболу и графически
изображается той же параболой, что и
 ,
но в отличие от последней имеет вершину
не в начале координат, а в некоторой
точке
,
но в отличие от последней имеет вершину
не в начале координат, а в некоторой
точке
 ,
координаты которой вычисляются по
формулам:
,
координаты которой вычисляются по
формулам:
 где
где
 —
дискриминант
—
дискриминант
Ось
её симметрии проходит через вершину
параллельно оси ординат, при a>0 (a<0)
фокус лежит на этой оси над (под) вершиной
на расстоянии a/4, а директриса — под
(над) вершиной на таком же расстоянии и
параллельна оси абсцисс. Уравнение
может
быть представлено в виде
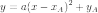 ,
а в случае переноса начала координат в
точку
каноническим
уравнением. Таким образом для каждого
квадратного уравнения можно найти
систему координат такую, что в этой
системе оно представляется каноническим.
При этом
,
а в случае переноса начала координат в
точку
каноническим
уравнением. Таким образом для каждого
квадратного уравнения можно найти
систему координат такую, что в этой
системе оно представляется каноническим.
При этом