40. Логарифм к.Ч. (последняя формула)
Определение и свойства
Для комплексных
чисел логарифм определяется так
же, как вещественный. На практике
используется почти исключительно
натуральный комплексный логарифм,
который обозначается 
и
определяется как решение 
уравнения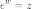 
(другие,
эквивалентные данному, варианты
определения приведены ниже).
В
поле комплексных чисел решение этого
уравнения, в отличие от вещественного
случая, не определено однозначно.
Например, согласно тождеству
Эйлера, 
;
однако также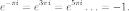 
Это
связано с тем, что показательная
функция вдоль мнимой оси является
периодической (с периодом 
),
и одно и то же значение функция принимает
бесконечно много раз. Таким образом,
комплексная логарифмическая
функция 
является многозначной.
Комплексный нуль не имеет логарифма, поскольку комплексная экспонента не принимает нулевого значения. Ненулевое можно представить в показательной форме:
Тогда находится по формуле:
Здесь 
—
вещественный логарифм, 
—
произвольное целое
число. Отсюда вытекает:
-
Комплексный логарифм существует для любого
,
и его вещественная часть определяется
однозначно, в то время как мнимая
часть имеет бесконечное множество
значений, различающихся на целое
кратное 
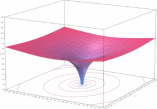
Вещественная часть комплексного логарифма
Из
формулы видно, что у одного и только
одного из значений мнимая часть находится
в интервале 
Это значение называется главным
значением комплексного
натурального логарифма. Соответствующая
(уже однозначная) функция называется
главной
ветвью логарифма
и обозначается 
.
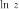Иногда через
также
обозначают значение логарифма, лежащее
не на главной ветви. Если
—
вещественное число, то главное значение
его логарифма совпадает с обычным
вещественным логарифмом.
Из приведенной формулы также следует, что вещественная часть логарифма определяется следующим образом через компоненты аргумента:
На
рисунке показано, что вещественная
часть как функция компонентов
центрально-симметрична и зависит только
от расстояния до начала координат. Она
получается вращением графика вещественного
логарифма вокруг вертикальной оси. С
приближением к нулю функция стремится
к 
Логарифм отрицательного числа находится по формуле:
