30. Свойства статистических оценок параметров распределения: несмещённость, эффективность, состоятельность.

Пусть требуется изучить количественный признак ГС. В распоряжении исследователя имеется выборка объемом n этого количественного признака ; ; … ; Рассматривая эти наблюдения как независимые случайные величины ; ; … ; можно сказать, что найти СТАТИСТИЧЕСКУЮ ОЦЕНКУ НЕИЗВЕСТНОГО ПАРАМЕТРА это значит найти функцию от наблюдаемых значений, которая и дает приближенное значение оцениваемого параметра.

Для того, чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны удовлетворять некоторым требованиям.

Пусть - статистическая оценка неизвестного параметра («тета»)

1. ОПР – НЕСМЕЩЁННОЙ называют статистическую оценку математическое ожидание которой равно оцениваемому параметру при любом объеме выборки т.е. 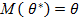ОПР – СМЕЩЁННОЙ называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Оценка должна быть несмещенной.

2. ОПР – ЭФФЕКТИВНОЙ называют статистическую оценку, которая имеет наименьшую возможную дисперсию (при заданном объеме выборки n)

3. ОПР – СОСТОЯТЕЛЬНОЙ называют статистическую оценку, которая при 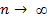стремится к оцениваемому параметру.

37. Нормальный закон распределения. Формула плотности вероятности.

Среди непрерывных распределений наиболее важную роль играет нормальное распределение, которое также называют законом Гаусса.

Плотность вероятности нормального распределения:

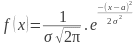
Где а – это математическое ожидание, σ – это среднее квадратическое отклонение случайной величины

38. Свойства кривой нормального закона распределения:

1. Определена на всей числовой оси

2. Принимает только положительные значения

3. Ось Ох служит горизонтальной асимптотой графика

4. График функции симметричен относительно точки х=а

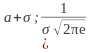5. Точки , ) – являются точками перегиба

График этой функции: