III. Использование расширенного алгоритма Евклида.

Шаги алгоритма:

В алгоритме все операции производятся над целыми числами. Под обозначением ]k[ будем понимать взятие от числа k только целой части, без округления.

На вход алгоритма подаются: числа aZ и mN, (a, m) = 1.

На выходе ожидается число a^-1 = .

1. Ввод числа a и модуля m, нормирующего результат.

2. Если a=0 или m=0 или m=1, то были заданы некорректные параметры.

3. Задаются вектора U={u1, u2, u3}, V={v1, v2, v3}. U={0, 1, m};V={1, 0, a}.

4. Пока u3≠1 и u3≠0 и v3 ≠0 выполняются следующие действия:

а) найти u3/q3: q = [u3/v3];

б ) для  i  1,3

- находится значение выражения t = u_i - v_i·q;

- u_i присваивается значение v_i-1;

- v_i присваивается новое значение: v_i = t;

5. Если u3≠1, то обратный элемент не существует, выход.

6. Если u3=1, то в переменной u1=a⁻¹. Если u1<0, то осуществляется приведение результата к положительному числу: u1 = m + u1 = a^-1

10. Первообразные корни

Число a, где (a, m) = 1, называется первообразным корнем по модулю m, если показатель a по этому модулю равен φ(m), то есть P(a) = φ(m).

Таким образом, первообразным элементом является число a, для которого выполняется сравнение: a^φ(m) =1 mod m, где φ(m) = P_m(a).

Существует следующий переборный вариант поиска первообразных элементов. В качестве кандидатов в первообразные элементы

рассматриваются все числа a = 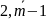, которые удовлетворяют следующим условиям:

1) взаимной простоты чисел a и m: (a, m) = 1;

2) a^φ(m) 1 mod m или a^φ(m) mod m=1;

3) для r =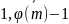 , являющегося делителем числа φ(m): a^r 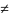1 mod m.

Число 1 в качестве варианта первообразного элемента не рассматривается, так как при  1ⁿ и  модуле φ(m) будет выполняться условие 1^φ(m)=1 mod m.

Теорема 1. Число a, a= 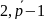, будет первообразным элементом по простому модулю p, если выполняется условие: A^(p-1/pi)≠1 mod p для i=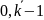 , где число p–1 представлено в виде канонического разложения p–1=p_i^αi, на k простых сомножителей, α_i - натуральные числа.

Теорема 2. Число первообразных корней, принадлежащих диапазону

a=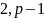 , равно:

- φ(p-1), если модуль p - простое число;

- φ(φ(m)), если модуль m - составное число.

Теорема 3. Если a - первообразный элемент по (простому и составному) модулю m, то остальные первообразные элементы могут быть найдены как числа a^k: (a^k mod m, φ(m)) = 1 и k≥2, k-целое.

Теорема 4. Пусть p - простое число. Если a является первообразным элементом по составному модулю p^α (α ≥ 1), то число a будет первообразным элементом и по модулю p.

Теорема 5. Пусть p - простое число. Если a - первообразный элемент по модулю p, то первообразным элементом также являются:

- число a по составному модулю p^k, если выполняются условия k≥2 и a^{(p-1)p^(k-2)} ≠1 mod p^k;

-одно из amodp² или (a+p)mod p².

Теорема 6. Пусть p - простое число. Если a - первообразный элемент по модулю p², то a является первообразным элементом по модулю p^k, k ≥ 2.

Теорема 7. Любой нечетный первообразный элемент по модулю p^k является первообразным корнем и по модулю 2p^k, где p - простое число и k ≥ 1-целое.

Теорема 8. Первообразные элементы по составному модулю m

существуют тогда и только тогда, когда:

1) m = p^k,

2) m = 2p^k, где p - простое число и k ≥ 1 - целое.

Теорема 9. Первообразный элемент существует тогда и только тогда, когда модуль m{2, 4, p^k, 2p^k}, где p - простое число и k ≥ 1 - целое.

14. Вычисление в поле GFC(2^n) обратных элементов

Обратный элемент в конечном поле GF(2ⁿ) используется как вспомогательный элемент при делении некоторого многочлена A(x) на многочлен B(x) в поле GF(2ⁿ) по полиному-модулю P(x). Результирующий полином C(x) будет получен как C(x)=A(x)*B^-1(x) mod P(x), где B^-1(x) - обратный элемент для многочлена A(x).

Одним из способов получения обратного элемента в поле полиномов является использование функции Эйлера. Понятие функции Эйлера по аналогии переносится из теории чисел в поле GF(2ⁿ)

Пусть задан неприводимый модуль-полином P(x). Функция Эйлера в поле GF(2ⁿ) будет задавать число взаимно простых с P(x) полиномов. Так как P(x) является неприводимым, то функция Эйлера φ(P(x)) = 2ⁿ-1. Тогда, применяя функцию Эйлера, обратный элемент будет вычисляться как

A^-1(x) = A^(P(x))-1(x) mod P(x) = A^{(2^n-2)}(x) mod P(x).

Обратный элемент в поле GF(qⁿ), где q - простое число, также можно вычислить и по модификации алгоритма Евклида, находящей переменные выражения α·a+β·b=НОД(a, b), только вместо чисел в формулу будут подставляться полиномы. Для нахождения обратного элемента g⁻¹(x) для полинома g(x) по полиному-модулю f(x) в качестве решаемого уравнения используется g⁻¹(x)g(x)+t(x)f(x) = 1, где g⁻¹(x), g(x), t(x), f(x)GF(qⁿ).