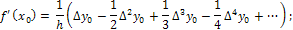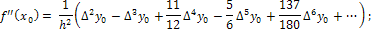5 Билет

1ч.

6 Билет

2Ч.Приближённые вычисления с помощью дифференциала

Формулу

задающую определение дифференциала, можно записать в виде приближённого равенства

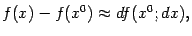
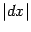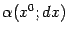если считать (при малых   ) значение бесконечно малой величины   много меньшим, чем   . Перенося 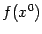  в правую часть, получаем:

где   . С учётом выражения дифференциала через частные производные, находим, что

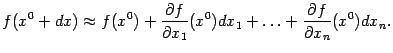
Эту формулу можно применять для приближённого вычисления значений функции 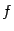  в точках   , если известны значения   и её частных производных 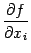  в точке   .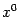

Пример 7   Пусть требуется приближённо вычислить значение

Рассмотрим функцию

и будем трактовать числа 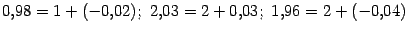  как малые отклонения на 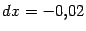  ,   , 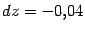  от "круглых" значений   .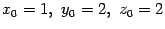

Поскольку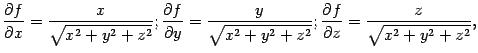

то дифференциал функции равен

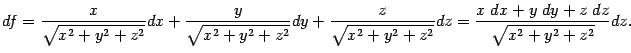
Значение функции в точке 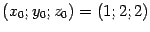  равно 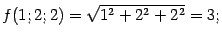  значения частных производных равны

Поэтому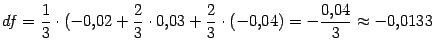

И

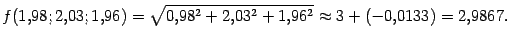
7 Билет

2ч.

Интерполяционная формула Ньютона дает точный результат только в том случае, если в одном из столбцов таблиц разностей всюду получается нуль (это имеет место, если заданная функция - полином). Если значения разностей в каком-либо столбце отличны от нуля, но достаточно малы, формула дает приближенный результат.

Обозначив  , представляют формулу Ньютона в виде

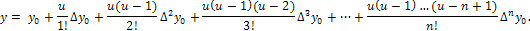
Практически сохраняют в правой части формул столько членов, чтобы при добавлении новых членов оставались неизменными те десятичные знаки, которые обеспечивают нужную точность результата. При вычислении значений, относящихся к последним срокам разностной схемы, применяется вторая интерполяционная формула Ньютона:

где

Из формулы Ньютона получаем