1 Билет

1ч. Дифференциальные уравнения — это соотношение вида F(x1,x2,x3,..,y,y',y'',...y(n)) = 0, связывающее независимые переменные x1,x2,x3,... функцию y этих независимых переменных и ее производные до n-го порядка. При этом функция F определена и достаточное число раз дифференцируема в некоторой области изменения своих аргументов.

Порядок дифференциального уравнения — это порядок старшей входящей в него производной.

Общее решение дифференциального уравнения — это соотношение вида y = y(x,C1,C2,C3,...Cn), зависящее от n произвольных постоянных.

Частное решение дифференциального уравнения — это общее решение при заданных значениях постоянных C1,C2,C3,...Cn.

Задача коши формулируется следующим образом:

Найти y = y(x), удовлетворяющую уравнению

y^’ = f(x,y) для x  [a,b] при заданном начальном условии y(a) = y₀.

Формула:

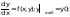
Примеры

1. – уравнение первого порядка;

– уравнение второго порядка;

– уравнение пятого порядка.

2. – решение, так как

3.Уравнение имеет решение:

.

4. Рассмотрим уравнение: . Отсюда или .

Поэтому , где С – произвольная постоянная.

– общий интеграл; – общее решение.

5. Уравнение . Его общее решение . Положим С=2, тогда – частное решение.

6. Уравнение имеет два общих решения: 1) 2)

Решение: 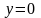есть частное по отношению к первому и особое по отношению ко второму общему решению.

7. . Общее решение .

2ч. Дискретной величиной(прерывной) называется: Случайная величина Х называется ,если множество ее значений конечное или бесконечное, но счетное.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями.

Выборочная средняя - значение Х выборки, случ величина, то математическое ожидание m(Х) равно выборочной средней:

2 Билет

1ч.

Дифференциальные уравнения 1-го порядка с разделяющимися переменными.

Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида (3.1)

или уравнение вида (3.2)

Для того, чтобы в уравнении (3.1) разделить переменные, т.е. привести это уравнение к так называемому уравнению с разделенными переменными, произвести следующие действия:

Теперь надо решить уравнение g(y)= 0. Если оно имеет вещественное решение y=a, то y=a тоже будет решением уравнения (3.1).

Уравнение (3.2) приводится к уравнению с разделенными переменными делением на произведение :

, что позволяет получить общий интеграл уравнения (3.2): . (3.3)

Интегральные кривые (3.3) будут дополнены решениями , если такие решения существуют.

2ч.

Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X)=M(X-M(X))²

Свойства дисперсии:

1)D(C)=0, где С-постоянная величина;

2)D(X)>0, где Х- случайная величина;

3)D(C•X)=C²•D(X), где С-постоянная величина;

4)D(X+Y)=D(X)+D(Y), где X,Y- независимые случайные величины;

Для вычисления дисперсии часто бывает удобно пользоваться формулой:

D(X)=M(X²)-(M(X))²,

_n

где М(Х)=∑ x_i²р_i= x₁²р₁ + x₂²р₂+…+ x_n²р_n

ⁱ⁼¹

Пример. Дискретная случайная величина Х задана законом распределения:

х	-1	0	1	2	3
р	0,1	Р2	0,3	0,2	0,3

Найти Р₂, функцию распределения F(x) и построить ее график, а также M(X),D(X), σ(Х).

Решение: Так как сумма вероятностей возможных значений случайной величины Х равна 1, то

Р₂=1- (0,1+0,3+0,2+0,3)=0,1

Найдем функцию распределения F(х)=P(X<x).

Геометрически это равенство можно истолковать так: F(х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Если х≤-1, то F(х)=0, т.к. на (-∞;х) нет ни одного значения данной случайной величины;

Если -1<х≤0, то F(х)=Р(Х=-1)=0,1, т.к. в промежуток (-∞;х) попадает только одно значение x₁=-1;

Если 0<х≤1, то F(х)=Р(Х=-1)+ Р(Х=0)=0,1+0,1=0,2, т.к. в промежуток

(-∞;х) попадают два значения x₁=-1 и x₂=0;

Если 1<х≤2, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)= 0,1+0,1+0,3=0,5, т.к. в промежуток (-∞;х) попадают три значения x₁=-1, x₂=0 и x₃=1;

Если 2<х≤3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)= 0,1+0,1+0,3+0,2=0,7, т.к. в промежуток (-∞;х) попадают четыре значения x₁=-1, x₂=0,x₃=1 и х₄=2;

Если х>3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)+Р(Х=3)= 0,1+0,1+0,3+0,2+0,3=1, т.к. в промежуток (-∞;х) попадают четыре значения x₁=-1, x₂=0,x₃=1,х₄=2 и х₅=3.

Итак,

0 при х≤-1,

0,1 при -1<х≤0,

0,2 при 0<х≤1,

F(x)= 0,5 при 1<х≤2,

0,7 при 2<х≤3,

1 при х>3

Изобразим функцию F(x)графически :

Найдем числовые характеристики случайной величины:

_n

М(Х)=∑ x_κр_κ =x₁р₁ + x₂р₂+…+ x_nр_n

κ=1

M(X)=-1•0,1+0•0,1+1•0,3+2•0,2+3•0,3=1,5

_n

D(X)= ∑ x²_κр_κ –(M(X))² = x²₁р₁ + x²₂р₂+…+ x²_nр_n –(M(X))²

κ=1

D(X)=(-1)² •0,1+1²•3+2²•0,2+3²•0,3-(1,5)²=1,65

^≈1,2845.