
- •1)Классификация каналов электросвязи
- •2) Линейные и нелинейные модели каналов.
- •3)Классификация каналов связи
- •4) Понятие непрерывного, дискретного и непрерывно-дискретного канала связи.
- •5) Детерминированные и случайные каналы.
- •6. Преобразование энергетических характеристик детерминированных сигналов.
- •4.3.7. Аддитивные помехи в канале
- •8.Идеальный непрерывный канал без помех. Канал с аддитивным гауссовским шумом
- •9.Непрерывный канал. Канал с неопределённой фазой сигнала и аддитивным шумом. Однолучевой канал с замираниями.
- •10.Канал с межсимвольной интерференцией и аддитивным шумом. Чем определяется память канала с мси?
- •11.Дискретный симметричный канал без памяти. Канал со стиранием.
- •12.Дискретные каналы с памятью.
- •13.Модели непрерывных каналов, заданные дифференциальными уравнениями.
- •Прием сигналов.
- •1.Задачи синтеза оптимальных демодуляторов. Критерии качества и правила приема дискретных сообщений.
- •2.Оптимальные алгоритмы приема при полностью известных сигналах(когерентный прием).
- •3.Оптимальный приемник с согласованным фильтром
- •4.Помехоустойчивость оптимального когерентного приема.
- •5.Какое правило приема преимущественно применяют в технике связи и почему?
- •6.Что понимают под согласованным фильтром? в какой момент времени на выходе сф обеспечивается максимальное отношение сигнал / шум и чему оно равно?
- •7.Какие основные блоки содержит корреляционная схема оптимального когерентного приема в канале с аддитивным стационарным бгш?
- •8 Обработка сигналов в каналах с межсимвольной интерференцией
- •9 Приём сигналов с неопределённой фазой (некогерентный приём)
- •11. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- •7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- •13 В чем смысл разнесенного приема сигналов и какие виды разнесения вы знаете?
- •10 Приём дискретных сообщений в условиях флуктуациифаз и амплитуд сигналов
- •Кодирование
- •1)Классификация методов кодирования. Конструктивные методы кодирования источников сообщений.
- •2) Вероятность ошибки оптимального декодирования для кодов с фиксированной длиной блоков (экспоненты вероятностей ошибок)
- •3)Коды с гарантированным обнаружением и исправлением ошибок
- •4)Линейные двоичные коды для обнаружения и исправления ошибок. Важные подклассы линейных двоичных кодов.
- •5)Какие классы кодов (по назначению) вы знаете? в чем заключается метод укрупнения алфавита?
- •6. Конструктивные алгоритмы исправления ошибок линейными кодами.
- •7.Пояснить различие между равномерным и неравномерным кодированием. Дайте определение префиксного кода.
- •8.Пояснить различие между линейным и нелинейным кодом. Дайте определение систематического кода.
- •9.Что такое избыточность помехоустойчивого кода? Что такое относительная скорость помехоустойчивого кода?
- •10.Что такое расстояние по Хэммингу и ее кодовой комбинации?
- •Что такое минимальное расстояние кода? Как упрощается процедура отыскания минимального расстояния для линейного кода?
- •Как связаны минимальное расстояние кода, число исправляемых и число обнаруживаемых ошибок?
- •Что такое декодирование по максимуму правдоподобия и по минимуму Хемминговского расстояния? Когда эти правила совпадают?
- •14.В чем состоит табличным метод кодирования, декодирования с обнаружением ошибок, декодирования с исправлением ошибок? Почему табличные процедуры не пригодны для длинных кодов?
- •15. Итеративные и каскадные коды
- •16. Системы с обратной связью
- •Система с обратной связью может достаточно полно характеризоваться двумя величинами:
- •Помимо описанных здесь трёх основных протоколов функционирования системы рос существует также много других вариантов1).
- •17. Как использовать помехоустойчивый код в системах с обратной связью?
- •Критерии помехоустойчивости приема непрерывных сообщений.
- •Оптимальная оценка отдельных параметров сигнала.
- •3. Оптимальная демодуляция непрерывных сигналов.
- •§ 8.2 Задачи оптимальной оценки одного параметра.
8.Идеальный непрерывный канал без помех. Канал с аддитивным гауссовским шумом
МОДЕЛИ НЕПРЕРЫВНЫХ КАНАЛОВ СВЯЗИ
Для того чтобы дать математическое описание канала, необходимо и достаточно указать множество сигналов, которые могут быть поданы на его вход, и для любого допустимого входного сигнала задать случайный процесс (сигнал) на его выходе. Задать случайный процесс можно в той или иной форме его распределения вероятностей. Так, в непрерывном канале надо задать априорную плотность (многомерную) w[u] входного процесса U(t) на интервале анализа Ta и многомерную переходную плотность w[z/u], т.е. плотность реализации принимаемого случайного колебания Z(t) (сигнал + шум) при условии передачи реализации U(t).
Точное математическое описание любого реального канала обычно весьма сложное. Вместо этого используют упрощённые математические модели, которые позволяют выявить все важнейшие закономерности реального канала, если при построении модели учтены наиболее существенные особенности канала и отброшены второстепенные детали, мало влияющие на ход связи.
Рассмотрим наиболее простые и широко используемые математические модели каналов, начав с непрерывных каналов, поскольку они во многом предопределяют и характер дискретных каналов.
ИДЕАЛЬНЫЙ КАНАЛ БЕЗ ПОМЕХ
Канал отображается линейной цепью с постоянной передаточной функцией, обычно сосредоточенной в ограниченной полосе частот. Допустимы любые входные сигналы, спектр которых лежит в определённой полосе частот Fc, имеющие ограниченную среднюю мощность Рс (либо пиковую мощность Pпик).Эти ограничения характерны для всех непрерывных каналов, и в дальнейшем о них не говорится.
В идеальном канале выходной сигнал s(t) при заданном входном u(t) детерминирован и определяется согласно (4.25): s(t) = γu(t - τ), где γ - постоянный коэффициент передачи канала, τ - постоянная задержка. Эту модель иногда используют для описания кабельных каналов. Однако, строго говоря, она не пригодна для реальных каналов, в которых неизбежно присутствуют, хотя бы и очень слабые, аддитивные помехи.
КАНАЛ С АДДИТИВНЫМ ГАУССОВСКИМ ШУМОМ
Сигнал на выходе такого канала
Z(t) = γu(t-τ) + N(t) = s(t) + N(t), (4.48)
где N(t) — гауссовский аддитивный шум с нулевым математическим ожиданием и заданной корреляционной функцией. Чаще всего рассматривается белый гауссовский шум (БГШ) либо квазибелый (с равномерной спектральной плотностью в полосе спектра сигнала s(t)). Часто при анализе можно τ не учитывать, что соответствует изменению начала отсчёта времени на выходе канала. Некоторое усложнение модели (4.48) получается, если коэффициенты передачи γ и запаздывания τ считать известными функциями времени: Z(t) = y(t)u[t-j(t)] + N(t).
Такая модель удовлетворительно описывает многие проводные каналы, радиоканалы при связи в пределах прямой видимости, а также радиоканалы с медленными общими замираниями, при которых можно надёжно предсказать значения γ и τ.
9.Непрерывный канал. Канал с неопределённой фазой сигнала и аддитивным шумом. Однолучевой канал с замираниями.
Эта
модель отличается от модели (4.48) тем,
что в ней запаздывание является
случайной величиной. Для узкополосных
сигналов с учётом (4.44) выражение
(4.48) при постоянном γ и случайных τ можно
представить в виде
 ,
,
где
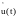 -преобразование
Гильберта от u(t);
θ = -w0τ
-случайная фаза.
Распределение вероятностей θ
предполагается заданным, чаще всего
равномерным на интервале от 0 до 2π.
Эта модель удовлетворительно
описывает те же каналы, что и предыдущая,
если фаза сигнала в них флуктуирует.
Такая флуктуация вызывается небольшими
изменениями протяжённости канала,
свойств среды, в которой проходит сигнал,
а также фазовой нестабильностью опорных
генераторов.
-преобразование
Гильберта от u(t);
θ = -w0τ
-случайная фаза.
Распределение вероятностей θ
предполагается заданным, чаще всего
равномерным на интервале от 0 до 2π.
Эта модель удовлетворительно
описывает те же каналы, что и предыдущая,
если фаза сигнала в них флуктуирует.
Такая флуктуация вызывается небольшими
изменениями протяжённости канала,
свойств среды, в которой проходит сигнал,
а также фазовой нестабильностью опорных
генераторов.
Однолучевой гауссовский канал с общими замираниями (флуктуациями амплитуд и фаз сигнала) также описывается формулой (4.48), но множительγ, как и фаза θ, считаются случайными процессами. Иными словами, случайными будут квадратурные компоненты X = γcosθ, Y=γsinθ.
При
изменении квадратурных компонент X,
Y
во времени принимаемое
колебание
 (4.49) Как отмечалось выше, одномерное
распределение коэффициента передачи
канала γ может быть рэлеевским или
обобщённым рэлеевским. Такие каналы
называют соответственно каналами с
рэлеевскими или обобщёнными рэлеевскими
(или райсовскими) замираниями. В рамках
общей гауссовской модели канала [14] γ
имеет четырёхпараметрическое
распределение. Модель однолучевого
канала с замираниями достаточно хорошо
описывает многие каналы радиосвязи
в различных диапазонах волн, а также
некоторые другие каналы.
(4.49) Как отмечалось выше, одномерное
распределение коэффициента передачи
канала γ может быть рэлеевским или
обобщённым рэлеевским. Такие каналы
называют соответственно каналами с
рэлеевскими или обобщёнными рэлеевскими
(или райсовскими) замираниями. В рамках
общей гауссовской модели канала [14] γ
имеет четырёхпараметрическое
распределение. Модель однолучевого
канала с замираниями достаточно хорошо
описывает многие каналы радиосвязи
в различных диапазонах волн, а также
некоторые другие каналы.
Многолучевой гауссовский канал с селективными по частоте замираниями обобщает модель (4.49):
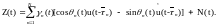 ,
(4.50)
,
(4.50)
где N
— число лучей в канале;
 -
среднее время задержки для n-го
луча. Многолучевая общая гауссовская
модель хорошо описывает многие каналы
радиосвязи. Для модели (4.50) условия
(4.46) не выполняется, если под ∆τ понимать
запаздывания между лучами.
-
среднее время задержки для n-го
луча. Многолучевая общая гауссовская
модель хорошо описывает многие каналы
радиосвязи. Для модели (4.50) условия
(4.46) не выполняется, если под ∆τ понимать
запаздывания между лучами.
