3. Оптимальная демодуляция непрерывных сигналов.

Определим условия оптимального приёма непрерывных сообщений. Пусть сообщение представляет собой некоторый стационарный процесс (первичный сигнал) с реализацией b(t). Он может непрерывно изменяться во времени и принимать любую форму.

Для простоты анализа будем считать, что функция b(t) принимает значения от -1 до +1, что реализации сообщения имеют конечную длительность Т и что их спектр практически ограничен частотами от 0 до F_c. При этих условиях функция b(t) может быть разложена по ортонормированному базису {ψ_k(t)} и представлена в виде усечённого ряда

(8.17)

где λ_k - случайные коэффициенты, определяющие передаваемое сообщение. При разложении в тригонометрический ряд Фурье λ_k пропорциональны составляющим спектра, а при разложении в ряд Котельникова - отсчётным зна­чениям 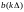функции b(t). Здесь . Таким образом, при известной системе базисных функций {ψ_k(t)} передача непрерывных сооб­щений b(t) эквивалентна передаче В значений коэффициентов (параметров) λ_k . Для передачи по каналу колебание b(t) преобразуется в сигнал s(t, b). Посколь­ку колебание (8.17) определяется параметрами λ_k (k = 1, 2, …. , В), то и сигнал зависит от этих параметров. Принятое колебание с учётом наложения помехи z(t) = s(t, b) + n(t) = s(t, λ) + n(t). (8.18)

Влияние помех приводит к тому, что каждый параметр λ_k будет принят с некоторой погрешностью . В результате оценка сообщения

где - погрешность воспроизведения сообщения b(t) (шум на выходе приёмника).

Таким образом, задача оптимального приёма непрерывного сообщения b(t) сводится к задаче совместного оптимального приёма совокупности многих па­раметров λ=( λ₁, λ₂, …, λ_B). Эта задача является обобщением рассмотренной в

§ 8.2 Задачи оптимальной оценки одного параметра.

По реализации z(t) необходимо восстановить переданное сообщение b(t) с возможно большей точностью, хотя бы при слабых помехах. Для этого необходимо на основе анализа принятого колебания z(t) найти максимум апо­стериорного распределения w(b|z), которое на основе формулы Байеса может быть представлено в виде

w(b|z) = kw(b)w(z|b), (8.20)

где k - постоянный коэффициент. Функция правдоподобия w(z|b), входящая в выражение (8.20), известна (для рассматриваемого гауссовского канала - это гауссовское распределение). Априорное распределение w(b) зависит от вида и характеристик передаваемых сообщений b(t).

Выбор конкретной модели априорного распределения w(b) является не столь существенным [26]. Роль начальных, априорных сведений уменьшается с увеличением объёма наблюдений. При большом объёме наблюдений алгорит­мы обработки сигналов получаются асимптотически одинаковыми, т.е. мало чувствительными к априорному распределению. Поэтому ограничимся рас­смотрением модели равномерного распределения w(b) = const. В этом случае решение задачи упрощается, так как согласно (8.20) апостериорное распреде­ление w(b|z) будет полностью определяться функцией правдоподобия w(z|b), которая для гауссовского канала определяется выражением, аналогичным (8.12):

Согласно этому выражению максимуму функции правдоподобия w(z|b), а следовательно, и функции w(b|z) соответствует минимум по b(t) интеграла

Значит, оптимальный приёмник должен воспроизводить сообщение b(t), которое соответствует, как и при передаче дискретных сообщений, тому из возможных сигналов s(t,b), который меньше других отличается в среднеквадратическом смысле от реализации сигнала z(t) на входе приёмника.

При отсутствии помех такой приёмник воспроизводит сообщение без иска­жений (без ошибок): z(t) = s(t, b(t)), b(t) = b(t) и , а при наличии помех ошибка минимальна.

Запишем (8.20) в другом виде, подобном (8.15):

где

Отсюда следует, что при известной априорной вероятности определение апостериорной вероятности сводится к вычислению функции q(b), т.е. скаляр­ного произведения принятого колебания z(t) на переданные (ожидаемые) сиг­налы s(t,b(t)).

<Во многих случаях для приближённого нахождения q(b) целесообразно применение про­стых следящих устройств. Рассмотрим принципиальную возможность построения таких уст­ройств. Подробное и более строгое обоснование на основе теории нелинейной фильтрации приводится в § 8.8.

При передаче непрерывных сообщений сигнал s(t,b(t)) не является полностью известным. Однако обычно имеется некоторая априорная информация об этом сигнале. Известны, на­пример, несущая частота, вид модуляции, ширина спектра сигнала и т.п. Часть информации можно получить в результате наблюдения над принятой реализацией сигнала z(f) за предшест­вующий промежуток времени. В результате имеется возможность определить оценку сигнала и вычислить функцию 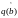для этой оценки:

Функцию можно найти с помощью фильтра с переменными параметрами (рис. 8.1) или схемы следящего коррелятора (рис. 8.2). Каждая из этих схем имеет основной информационный канал, на выходе которого получается оценочное значение передавае­мого сообщения, и канал обратной связи, с помощью которого в схеме рис. 8.2 формируется опорный сигнал , а в схеме рис. 8.1 с помощью управляющего элемента (УЭ) произ­водятся изменения параметров фильтра СФ так, чтобы он был согласован с непрерывно из­меняющимся ожидаемым сигналом . В схеме рис. 8.2 с помощью УЭ изменяется мо­дулируемый параметр несущего колебания, формируемого генератором (Г).

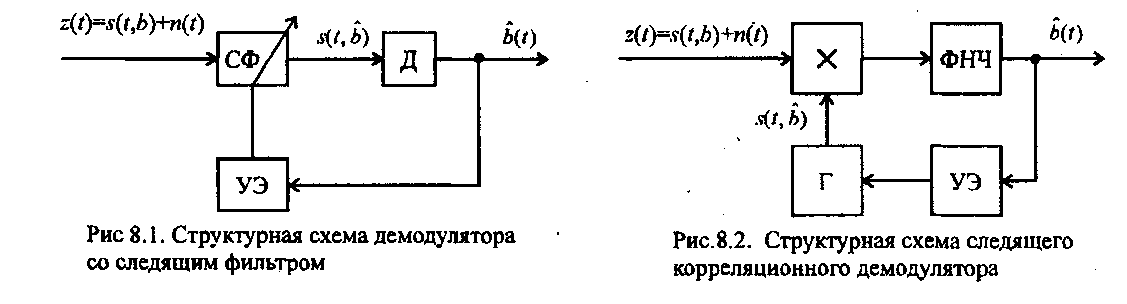
При частотной модуляции, например, этим параметром будет частота, при временной импульсной модуляции — сдвиг импульсов во времени и т.п. Фильтр нижних частот ФНЧ в этой схеме выполняет роль интегратора на интервале наблюдения Т, который связан с максимальной частотой F_c в спектре передаваемого сообщения соотношением Т = l/(2F_c).

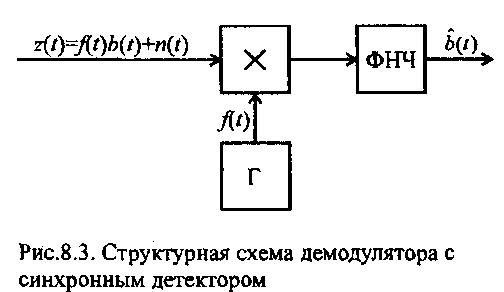
Рассмотренные схемы являются квазиоптимальными, поскольку получаемая оценка не является наилучшей возможной. При различных видах модуляции принцип сле­дящего приёма остаётся одним и тем же. Вид модуляции определяет параметр, за которым должно осуществляться слежение. Иначе говоря, оптимальный приёмник должен с наимень­шей ошибкой следить за передаваемым случайным колебанием b(t). Схемы следящего приёма позволяют практически реализовать помехоустойчивость, близкую к потенциальной. При ли­нейной модуляции, когда s(t,b(t)) = f(t)b(t), где f(t)- известная функция (несущее колебание), оптимальный демодулятор можно реализовать разомкнутой схемой с синхронным детектором (рис. 8.3)

>

Перейдём к определению помехоустойчивости систем связи при оптималь­ном приёме. Заметим, что эту потенциальную помехоустойчивость можно вы­числить, не уточняя структуры оптимального демодулятора. Для этого доста­точно знать, что он выдаёт решение , соответствующее минимуму (8.21).

Прежде чем приступить к выводу формул, определяющих потенциальную помехоустойчивость, напомним основные принципы классификации видов мо­дуляции при передаче непрерывных сообщений. В общем случае модуляция за­ключается в том, что множество сообщений (первичных сигналов) B(t) преоб­разуется (отображается) в множество вторичных сигналов S(t)=S[t,B(t)]. Этой записью подчеркивается, что значение сигнала S в некоторый момент t опреде­ляется в общем случае всем поведением сообщения B(t) на всей оси времени.

В частном случае, если сигнал S(t) в любой момент t зависит не от всего хода сигнала B(t), а только от его значения в момент t, то система модуляции называется прямой. В этом случае сообщение b(t) входит непосредственно в вы­ражение сигнала s(t). К прямым относится подавляющее большинство приме­няемых методов модуляции, например AM, БАМ и ФМ. Остальные системы модуляции, в которых S(t) зависит от общего поведения сигнала B(t), называ­ются непрямыми. Среди них особый интерес представляют интегральные систе­мы, в которых B(t) входит в выражение S(t) под интегралом.

Система модуляции называется линейной, если S(t) можно получить из B(t) с помощью линейных операций. Линейные системы могут быть прямыми (например, амплитудная - AM) и непрямыми (например, однополосная - ОМ).

Геометрически модуляцию можно рассматривать как отображение про­странства В сообщений в пространство сигналов S, а демодуляцию - как об­ратное отображение. При демодуляции помеха n(t) на входе приёмника ото­бражается в погрешность оценки сообщения (шум воспроизведения или шум на выходе приёмника) ε(t).

Рассмотрим приём непрерывного сообщения на фоне Б ГШ со спектраль­ной плотностью N₀. При достаточно слабом шуме n(t) погрешность (шум на выходе приёмника) представляет собой также гауссов-ский процесс со спектральной плотностью G_ε(f), которую и будем определять. Для. этого удобно воспользоваться геометрическим представлением. В про­странстве сигналов каждой реализации сигнала s(t,b(t)) при различных b(t) со­ответствует точка. Если s(b) зависит непрерывно от b (что имеет место во всех аналоговых системах связи), то все эти точки образуют некоторую кривую (рис. 8.4). Принятый сигнал z(t) является также точкой в пространстве сигналов, как правило, не лежащей на кривой s(b).максимально правдоподобная оценка соответствует тому сигналу, который изображается на сиг­нальной кривой точкой, ближайшей к точке z. Обозначим , где b(t) - действительно переданное сообщение. При малой помехе и, следова­тельно, малом отклонении отрезок между s(b) и 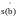можно аппроксимиро­вать прямой линией, которая является касательной к линии сигнала в точке s(b). Тогда представляет проекцию вектора n на эту прямую. В этом случае справедливо представление

(8.25)

Здесь n₁(t) - составляющая (координата) шумового вектора в пространстве сигналов, представляющая низкочастотный гауссовский эргодический процесс с нулевым МО и со спектральной плотностью N₀ в полосе частот от 0 до F_c, . Тогда с учётом (8.25) в единичной полосе частот

(8.26)

Поскольку процесс ∆b(t) (компонента шума на выходе приёмника) меняется значительно медленнее процесса , то

(8.27)

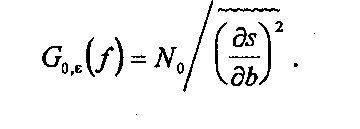(8.28)

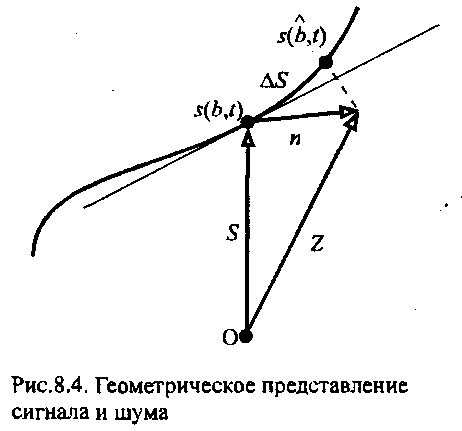
При прямых системах модуляции не зависит от частоты. Таким обра­зом, при прямых системах модуляции шум на выходе приёмника квазибелый, т.е. имеет равномерный спектр в полосе частот F_c. В случае интегральных систем сообщение B(t) входит в выражения сигнала под знаком интеграла: Так как

Следовательно СПМ шума на выходе приёмника для интегральных систем можно определить как СПМ производной ξ'(t). На основании известной теоремы о спектре производной

, где G_0ξ (f) определяется по формуле (8.28), если в послед­ней вместо ds/db подставить ds/dψ. Таким образом, для интегральных систем СПМ шума на выходе приёмника

(8.29)

т.е. СПМ помехи на выходе приёмника в интегральных системах пропорциона­лен квадрату частоты.

Все эти результаты справедливы для линейной модуляции или при произвольной модуляции для слабых помех, когда можно считать . Они ха­рактеризуют так называемые нормальные ошибки (см.§ 8.5).

Очевидно, мощность шума на выходе приёмника в полосе частот от нуля до F_c будет

С другой стороны, мощность Р_b сообщения на выходе приёмника, равная , можно выразить через пик-фактор сообщения . Полагая, что сообщение нормировано и ,получаем (8.30)

Тогда отношение мощностей сигнала и шума на выходе приёмника

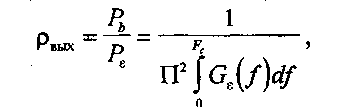(8.31)

а выражение для выигрыша g и обобщённого выигрыша g' в соответствии с оп­ределениями (8.3) и (8.4) можно записать так: 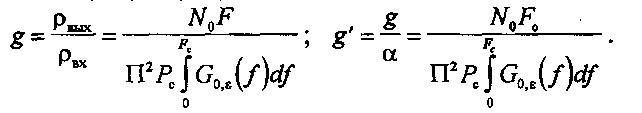(8.32)

Для гармонического сигнала , а для телефонного сообщения П≈З.

Используя теорему Шеннона (см. § 6.7), можно найти максимальные воз­можные значения выигрыша и обобщённого выигрыша при заданных парамет­рах системы связи. Рассмотрим этот вопрос для наиболее простого случая, ко­гда непрерывное сообщение представляет гауссовский процесс с равномерным спектром в полосе частот F_c (квазибелый шум), а в канале существует аддитив­ная помеха в виде квазибелого шума в полосе F с односторонней спектральной плотностью N₀. Согласно теореме Шеннона передача сообщения с заданным значением возможна в случае, когда Н'_ε(В) < С'. Здесь Н'_ε(В) - эп­силон-производительность источника, которая в данном случае согласно (§ 6.3.2) равна F_c logρ₀, а С' - пропускная способность гауссовского канала, равная согласно (6.83)

где F - полоса пропускания канала и в общем случае F ≠F_c.

В гипотетической идеальной системе связи, в которой полностью использу­ется пропускная способность канала и ρ_вых = ρ₀

F_clog ρ_вых=Flog(l + ρ_вх) (8.33)

В реальных системах связи обычно удаётся лишь частично использовать пропускную способность канала. Назовем эффективностью ηсистемы связи отношение эпсилон-производительности источника к пропускной способности канала, при которой обеспечивается заданная верность, т.е. ρ_вых = ρ_0. Для та­кой реальной системы вместо (8.33) имеем (8.34)

Из выражений (8.33) и (8.34) видно, что при ηF> F_c можно обеспечить вы­сокую верность (большое значение ρ_вых) при относительно малых ρ_вх, т.е. по­лучить большой выигрыш g.

Таким образом, выигрыш достигается в результате обмена ширины спектра на динамический диапазон, о чём говорилось в § 1.2. Большой выигрыш мож­но получить только при большом отношении Заметим, что большой выигрыш может иметь место и при малой эффективности η, и наоборот. Сле­довательно, при оценке различных систем связи необходимо учитывать по крайней мере два показателя: эффективность и помехоустойчивость. Совокуп­ность этих двух показателей составляет достаточно полную характеристику сис­темы.

Наилучшей считается система, которая обеспечивает наибольшую помехо­устойчивость при заданной эффективности либо наибольшую эффективность при заданной помехоустойчивости.

Для идеальной системы η = 1, и из (8.33) следует

(8-35)

Отсюда при ρ>>1 получаем

(8.36)

Таким образом, в идеальной системе выигрыш g возрастает с увеличением α по экспоненциальному закону. Никакая реальная система не может обеспе­чить при заданном а более высокую помехоустойчивость, чем идеальная.