Помимо описанных здесь трёх основных протоколов функционирования системы рос существует также много других вариантов1).

Заметим, что важным положительным свойством систем с обратной связью является их адаптивность. Действительно, как это следует из

,

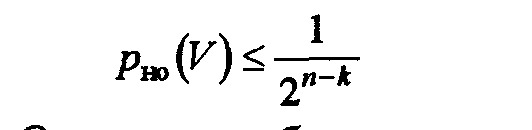p_HO{V) мо­жет быть сделана весьма малой для любых состояний канала в отличие от

р_0Д(У) при использовании лишь исправления ошибок. Поэтому если состояние канала связи (например, р в 2СК) изменяется, причём иногда вплоть до обрыва (р = 1/2), то p_HO{V) всё равно оказывается достаточно малой, а скорость переда­чи будет значительно изменяться в соответствии с (7.81) или (7.82), подстраи­ваясь (адаптируясь) к состоянию канала и обеспечивая достаточно высокую среднюю скорость передачи. В системах с обратной связью можно использо­вать также и частичное исправление ошибок, что может существенно увеличить сквозную эффективность, но приведёт к неизбежному усложнению аппаратно­го или программного обеспечения.

17. Как использовать помехоустойчивый код в системах с обратной связью?

В системе связи используются некоторые помехоустойчивые (например линейные блоковые) коды и для декодирования используются не значения дискретных символов, полученные после демодулятора, а значения элементов непрерывных сигналов, соответствующих переданным символам, или адекватные им достаточные статистики, например отсчёты на выходах согласованных фильтров.

Разделение операций демодуляции и декодирования на приемной стороне носит условный характер. Действительно, при использовании помехоустойчивого двоичного блочного кода с длиной блока п можно рассматривать п последовательных канальных сигналов (которые не являются независимыми и равновероятными, так как они связаны проверочными соотношениями кода) как один "составной" или "сложный" сигнал длительностью пТ .

Таким образом, получим систему, в которой для передачи 2^k сообщений используется 2^k "сложных" сигналов длительностью пТ каждый. Для указанных сигналов можно построить оптимальный приёмник, который обеспечивает минимально возможную вероятность ошибочного приёма сообщения, совмещая в себе функции демодулятора и декодера (объединяя операции демодуляции и декодирования). Он отображает каждую реализацию длительностью пТ на выходе канала в одно из 2^k сообщений, то есть реализует декодирование в широком смысле. Точно так же можно последовательно включённые кодер и модулятор заменить одним устройством, которое будет с каждым из 2^k сообщений сопоставлять сложный сигнал для передачи по каналу. Такое устройство выполняет кодирование в широком смысле.

Рассмотрим алгоритм работы оптимального приёмника кодированных сигналов. Будем считать, что элементарные двоичные сигналы на передаче противоположны и имеется канал с постоянными параметрами и БГШ. Тогда учитывая, что энергии всех 2^k сложных сигналов одинаковы, получаем

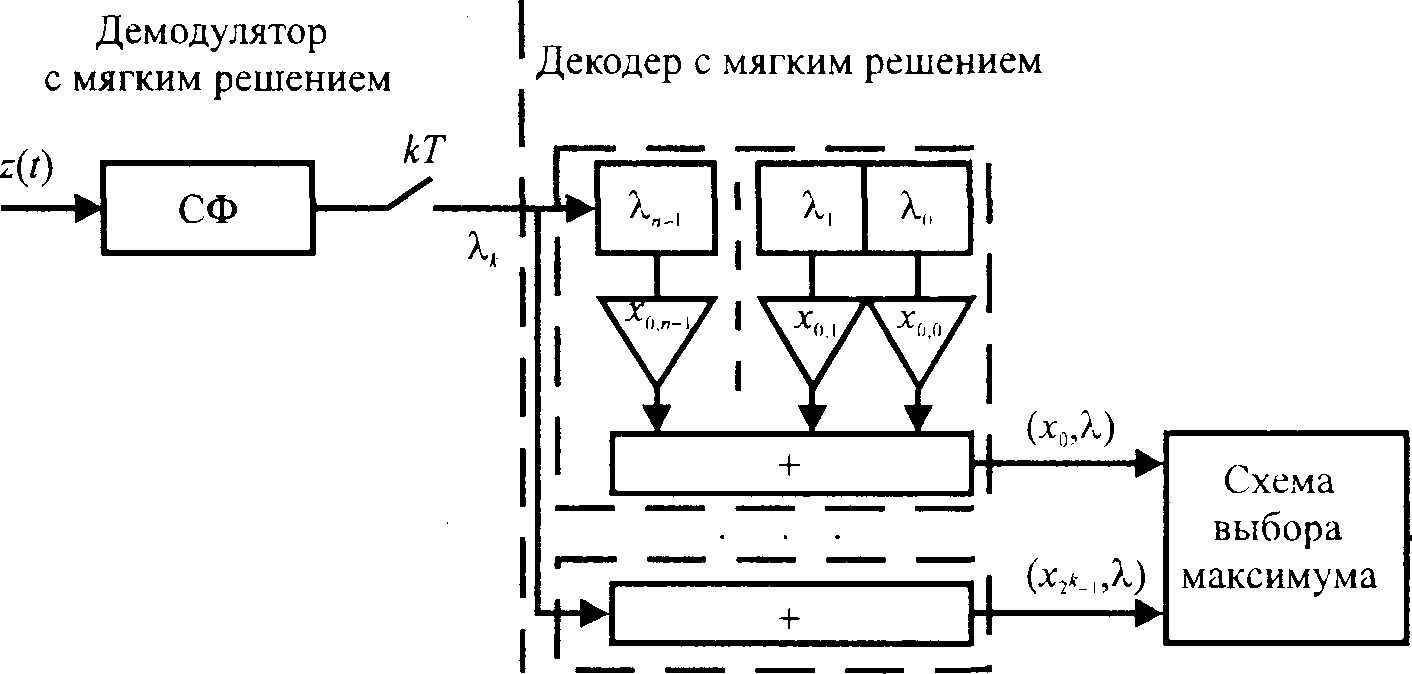
Рисунок 3.7 - Объединение операций демодуляции и декодирования

где 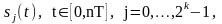— сложный сигнал, соответствующий j-й кодовой комбинации; , — один из двух противоположных сигналов, передаваемый в составе j-го сложного сигнала на i-й позиции и определяемый i-м кодовым символом s(t) задан на интервале длительностью Т. В соответствии с представленной формулой сначала по z(t) вычисляется вектор  = (₀, ..., _n-1) , компоненты которого могут быть получены как отсчёты (в моменты, кратные T) с выхода фильтра, согласованного с элементарным сигналом s(t); затем вычисляется скалярное произведение вектора  с каждым возможным кодовым вектором x_j = (x_0,j, ...,x_n-1,j) и принимается решение в пользу того кодового вектора, который обеспечивает максимальное значение скалярного произведения. Скалярное произведение (х_i, ) может быть найдено с помощью цифрового фильтра, как показано на рисунке 3.7.

Таким образом, оптимальный приёмник кодированных сигналов, (который использует информацию о входном непрерывном сигнале) можно представить как последовательное соединение демодулятора с мягким решением и декодера с мягким решением.

Из рисунка 3.8 видно, что разница между декодированием с мягким решением и декодированием с жёстким решением состоит в том, что жёсткий декодер работает только с вектором y = (y₀, ..., y_n-1), yi = sign(_i), а мягкий декодер использует дополнительную информацию о надёжности компонент вектора у, которую можно получить на основе анализа величин |_i|: чем больше величина |_i|, тем надёжнее принятое в выходном блоке демодулятора жёсткое решение у_i. Демодулятор, выдающий на выход дополнительную информацию о надёжности своих решений, называется демодулятором с мягким решением {выходом}, рисунок 3.8.

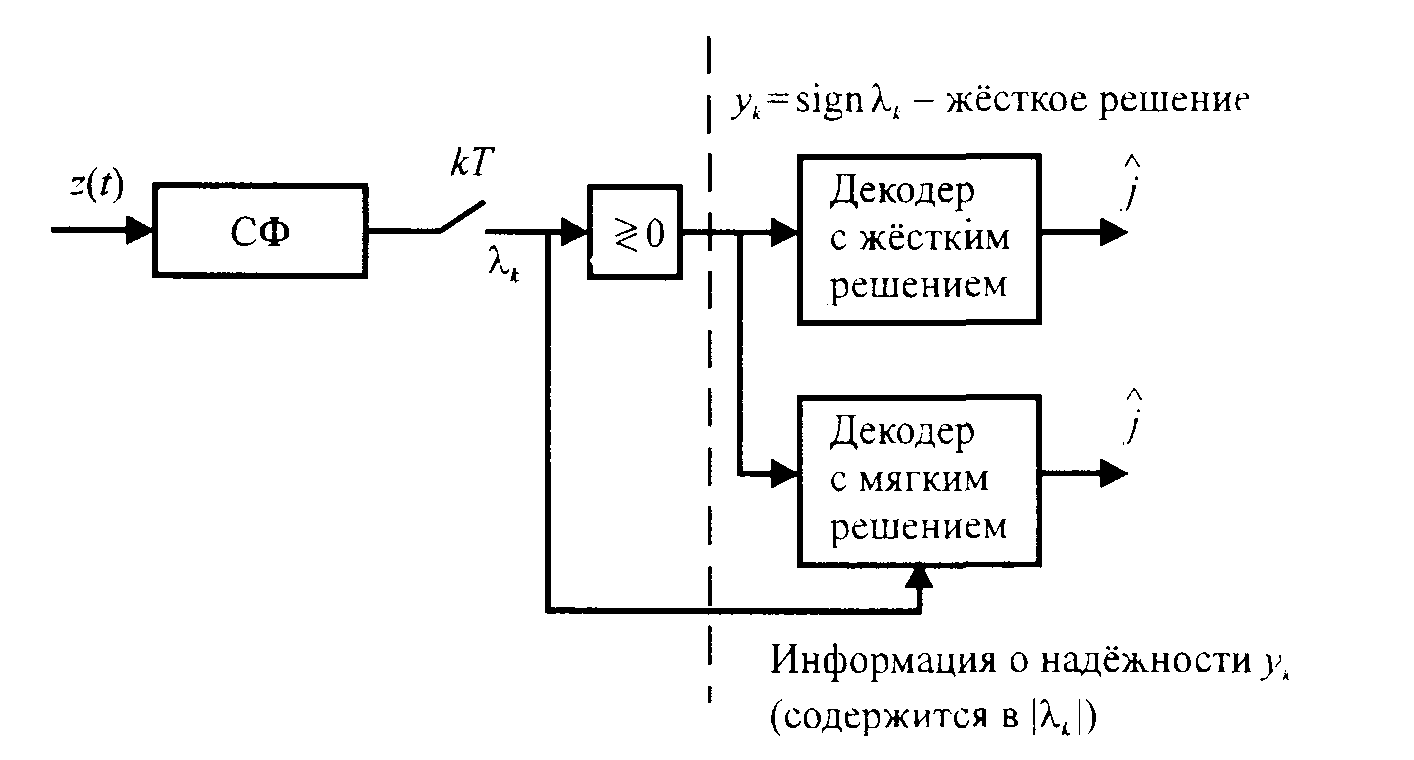
Рисунок 3.8 - Различие между декодированием с мягким и жёстким решением

Декодирование с мягким решением устраняет потери, связанные с принятием промежуточного решения в выходном блоке демодулятора (то есть с заменой _i на у_i). Оптимальным по помехоустойчивости алгоритмом мягкого декодирования является объединение операций демодуляции и декодирования (см. рисунке 3.7). С другой стороны, сложность декодера рисунке 3.7 значительна, поэтому предложено много алгоритмов декодирования с более простой реализацией, способных в той или иной мере учитывать информацию о надёжности решений, принимаемых демодулятором.

Поскольку при мягком декодировании используется более полная информация о принятых символах, то следует ожидать получения меньших вероятностей ошибок для того же самого кода, чем при жёстком декодировании. Очевидно, что для рассмотренной выше модели постоянного канала с аддитивной помехой в виде БГШ мы получаем алгоритм максимума правдоподобия, эквивалентный декодированию по минимуму евклидова расстояния. Причём если при передаче двоичных противоположных сигналов в таком канале связи оптимизация кода по-прежнему будет соответствовать максимизации минимального расстояния d, то для m-ичных кодов требуется максимизация минимального евклидова расстояния, что необязательно будет адекватно максимизации d.

Для мягкого декодирования также существуют экспоненты вероятностей ошибок и границы ошибок при известном спектре кодов. В последнем случае для двоичных противоположных сигналов в неискажающем канале с БГШ оптимальный алгоритм мягкого декодирования может обеспечить следующую границу для вероятности ошибки:

, (3.83)

где - отношение энергии элемента сигнала к спектральной плотности белого шума в канале связи; {N_i} — спектр весов кода.

Для мягкого декодирования также можно рассчитать ЭВК от применения кодирования, который будет, очевидно, превосходить ЭВК для жёсткого декодирования, причём для каналов с постоянными параметрами типичный выигрыш имеет порядок 2 дБ.

Для конструктивной реализации мягкого декодирования невозможно в чистом виде использовать алгебраические методы, хотя имеются некоторые их модификации приемлемые в этом случае, такие, например, как декодирование по минимуму обобщённого расстояния или мажоритарное декодирование. Наиболее перспективным для реализации мягкого декодирования (совместной демодуляции-декодирования), в том числе и для каналов с памятью, оказалось применение свёрточных кодов, которые допускают использование оптимального, но вместе с тем практически реализуемого алгоритма Витерби. Этот подход изложен в следующем параграфе данной главы.

18.Что такое синдром? Как он используется при декодировании с обнаружением ошибок и при декодировании с исправлением ошибок?

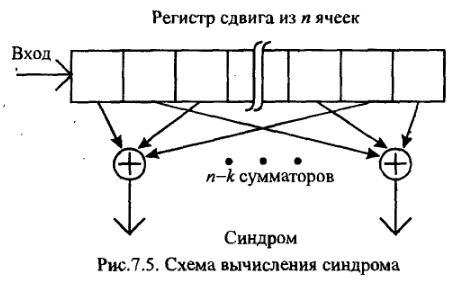
Пример обнаружения ошибки.

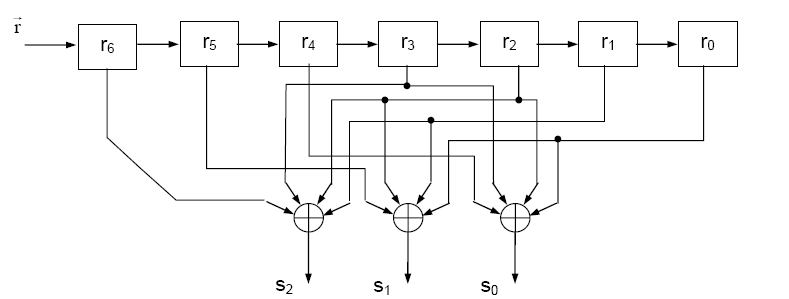
19.Как в матричной форме задать процедуры кодирования и вычисления синдрома для линейного кода?

Пример вычисления синдрома в матричной форме.

20.Как задаются процедуры кодирования и вычисления синдрома для полиномиальных кодов?

21. Сверточный (решеточный) код

Наиболее распространённым классом непрерывных кодов являются так называемые свёрточные коды, для которых операция формирования выход­ной последовательности по заданной входной последовательности является ли­нейной.

Структура двоичного свёрточного кода со скоростью R = n/k показана на рис:

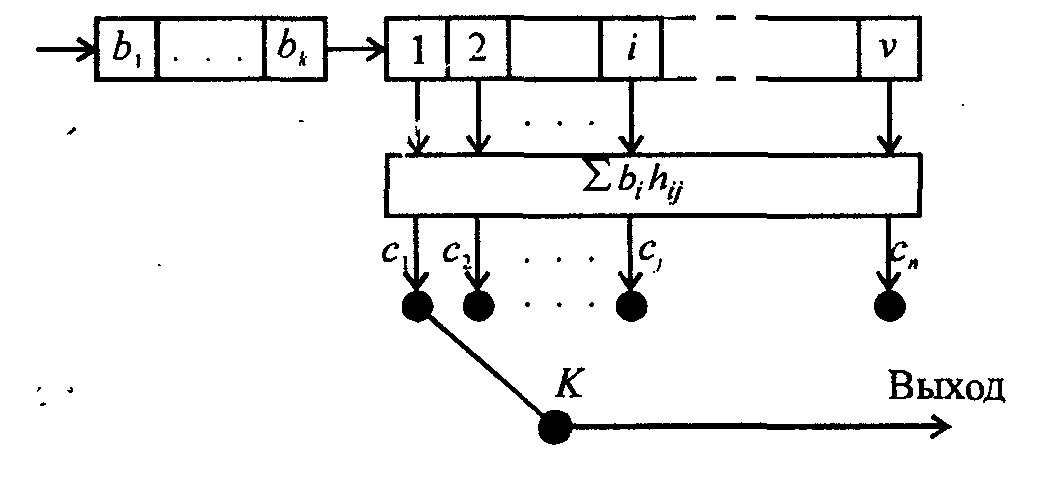
Свёрточный кодер состоит из сдвигового регистра, включающего v ячеек памяти, блока суммато­ров по mod 2, входы каждого из которых связаны с некоторыми выходами ячеек памяти реги­стра, определяемыми коэффициентами h_i,j=(0, l). Выходы сумматоров считываются при по­мощи коммутатора К и подаются в канал связи. Таким образом, на каждом такте в регистр сдвига последовательно поступает очередной блок из k информационных символов источника и одновременно он освобождается от k символов, содержащихся в его крайних правых ячей­ках памяти. На этом же такте формируются n выходных символов, которые последовательно считываются в канал связи. Таким образом, если v_и — скорость поступления символов в ко­дер, то для отсутствия растущих задержек во времени скорость передачи символов по каналу связи должна быть не меньше чем v_k= v_и*n/k откуда видно, что отношение n/k действительно определяет скорость свёрточного кода. Ве­личина v (или длина регистра) обычно на­зывается длиной кодового ограничения. (Возможно и другое, более общее представление свёрточного кодера в виде схемы с к регистрами сдвига с кодовыми ограничениями v, (i= 1, 2, …k.) На вход каждого из них подаётся один информаци­онный символ за время одного такта [13].)

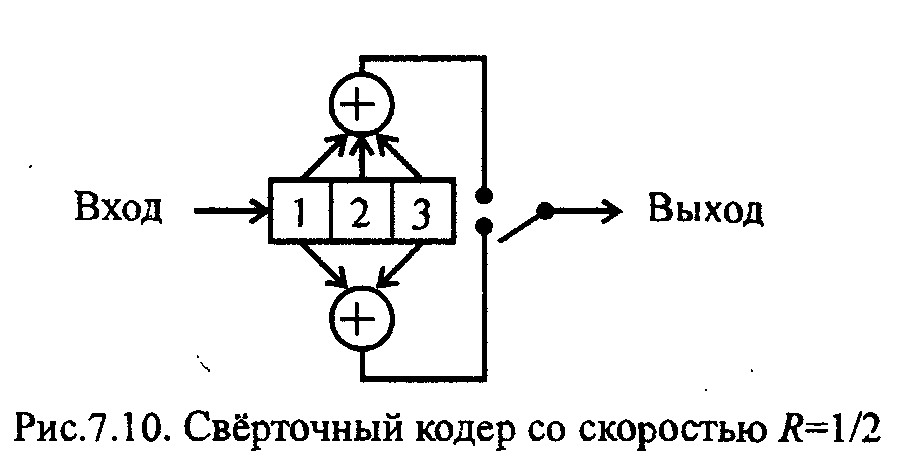
На рис показан частный случай свёрточного кода со скоростью 1/2 и

длиной кодового ограничения v = 3. При нулевой информационной последовательности вы­ходная кодовая последовательность также равна нулю. В табл. 7.5 приведён пример формиро­вания выходной последовательности для кодера, показанного на рис. Выходная последо­вательность кодера может быть представлена как цифровая свёртка входной информационной последовательности и импульсного отклика кодера (отсюда название кодов — свёрточные).

Сверточный код характеризуется следующими параметрами : относительной скоростью када R=k/n? и избыточностью x=l-R, где kиn — число информационных и кодовых символов, соответствующих одному такту работы кодера {для кодера рис. где R-1/2); длиной кодового

ограничения v (длина регистра кодера); порождающим полиномом кода, коэффициенты которых описывают связи сумматоров с ячейками регистра кодера (для верхнего сумматора g⁽¹⁾ = l+D+D², для нижнего сумматора g⁽¹⁾ = l+D²). Полиномы обычно записывают сокра­щённо, обозначая каждые три отвода (двоичных коэффициента) как одну восьмеричную циф­ру (код рис. обозначается (7,5)).

Кроме перечисленных выше параметров свёрточный код характеризуется свободным рас­стоянием d_CB, под которым понимают расстояние по Хеммингу между двумя полубесконеч­ными кодовыми последовательностями. Если две одинаковые информационные последова­тельности кодировать с помощью кодера, изображённого на рис. то соответствующие им кодовые последовательности будут совпадать друг с другом. Если в некоторый момент в од­ной информационной последовательности окажется символ 0, а в другой 1, то с этого момен­та кодовые последовательности будут отличаться друг от друга независимо от дальнейшего содержания информационных последовательностей. Минимальное расстояние по Хеммингу между любыми двумя полубесконечными кодовыми последовательностями с того момента, как соответствующие им информационные последовательности начинают различаться, назы­вается свободным расстоянием свёрточного кода d_Cb.

Свободное расстояние d_CB характеризует помехозащитные свойства свёрточного кода (аналогично тому как минимальное расстояние d характеризует помехозащитные свойства блочных кодов). Оно показывает, какое наименьшее число ошибок должно произойти в кана­ле для того, чтобы одна кодовая последовательность перешла в другую и ошибки не были об­наружены. Для кода, приведённого в нашем примере, свободное расстояние d_св = 5 .

Поиск хороших свёрточных кодов (с наибольшим d_CB при заданных R и v) обычно осу­ществляется методом перебора всех порождающих полиномов на ЭВМ. Свёрточные коды являются частным случаем (линейной реализацией) так называемых решётчатых кодов. Можно также полагать, что решётка является просто другим (иногда более удобным) способом представления и обычных свёрточных кодов. Решёткой называется ориентирован­ный граф с периодически повторяющейся структурой "ячеек". Каждая ячейка содер­жит колонки из одинакового числа вер­шин (узлов), соединённых ребрами. Меж­ду процедурой кодирования свёрточным кодом и решеткой имеется взаимно однозначное соответствие, которое задается кодом и решёткой имеется взаимно однозначное соответствие, которое задаётся следующими правилами:

• каждая вершина (узел) соответствует внутреннему состоянию кодера;

• ребро, исходящее из каждой вершины, соответствует одному из возможных символов источника (для двоичного источника из каждой вершины выходит два ребра — верхнее для 0 и нижнее для 1);

• над каждым ребром отмечены значения символов, передаваемых в канал связи, если кодер находился в состоянии, соответствующем данной вершине и источник выдал символ, соответствующий данному ребру;

• последовательность ребер (путь на решётке) — это последовательность сим­волов, выданных источником.

Так, если под состоянием кодера по­нимать содержимое двух последних ячеек памяти (2, 3) в регистре сдвига на рис. 2 то решётка с четырьмя состоя­ниями, соответствующая данному кодеру, будет иметь вид, показанный на рис.3 (решётка может отражать и нелинейный кодер, когда выходные символы не яв­ляются линейной функцией входных). Так же как и блоковые коды, свёрточные допускают представление в виде полу­бесконечных порождающих или прове­рочных матриц, однако представление в виде решётки оказывается более удобным для описания алгоритмов декодирования.

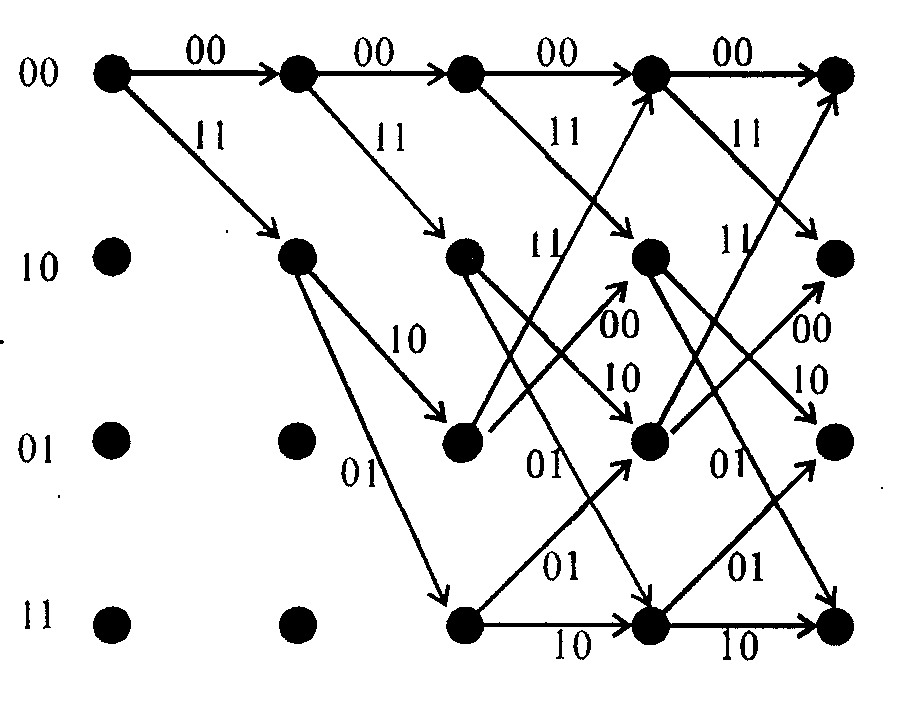
Свёрточные коды имеют следующие основные преимущества перед блоко­выми при их использовании для исправления ошибок.

1. Они не требуют синхронизации по блокам, а лишь синхронизации коммута­торов К (на передаче и приёме).

2. Если кодовое ограничение v выбр xb равным длине блокового кода, то ис­правляющая способность свёрточного кода оказывается больше, чем исправ­ляющая способность такого блокового кода (при наилучшем выборе обоих кодов).

3. Алгоритм декодирования свёрточных кодов допускает простое обобщение на случай мягкого декодирования, что обеспечивает дополнительный энергети­ческий выигрыш.

4. Свёрточные коды допускают простое объединение кодирования и модуляции (так называемая кодированная модуляция или сигнально-кодовые конструкции), что особенно важно при построении энергетически эффективных систем связи для каналов с ограниченной полосой частот.

Для оптимального декодирования свёрточных кодов в каналах без памяти часто используется рекуррентный алгоритм декодирования Витерби (АВ). Рас­смотрим его на примере мягкого декодирования в постоянном канале с адди­тивным белым гауссовским шумом.

П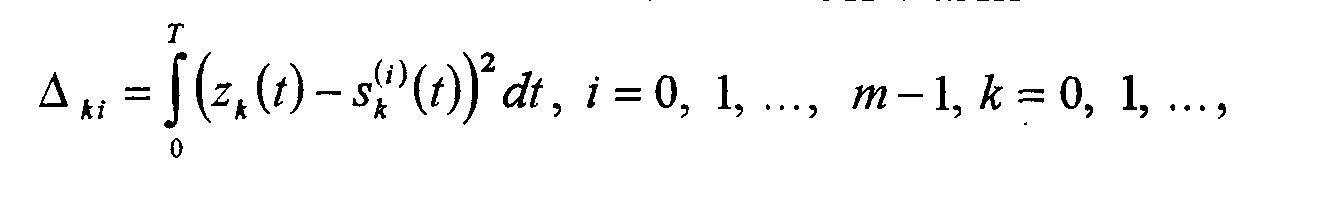 оскольку принимаемый сигнал на k-м тактовом интервале нам известен, то" можно вычислить евклидовы (или гильбертовы) расстояния между приня­тым сигналом и всеми возможными сигналами:

где s⁽ⁱ⁾_k(t) — ожидаемый в месте приёма сигнал, соответствующий i-му символу (для двоичных сигналов / = 0,1); z_k(t) — сигнал, принятый на k-м тактовом ин­тервале.

Т еперь можно каждому ребру решётки последовательно приписывать на k-х её звеньях значения _ki. Оптимальное по правилу максимального правдоподобия декодирование будет тогда соответствовать выбору такого пути на решётке (т.е. последовательности непрерывно продолжающихся

ребер), что окажется минимальной. Казалось бы, для решётки длины n (т.е. для последова­тельности переданных символов длиной n) нужно для этого перебрать 2" воз­можных вариантов, но в действительности это не так. Ключевой момент АВ состоит в том, что для каждой вершин на данном шаге (такте) имеется множе­ство метрик, соответствующих соединённым с ней ребрами вершинам на пре­дыдущем шаге можно оставить только одно ребро, которое минимизирует сум­му метрик на всех предыдущих шагах.

Сложность АВ определяется на каждом шаге числом сравнений метрик, со­единяющих все вершины, и оно ограничено величиной М², где М — число со­стояний решётки. Поскольку из схемы свёрточного кодера получаем, что M = 2^v-l, где v — число ячеек памяти регистра сдвига кодера, то видим, что сложность АВ экспоненциально зависит от длины кодовых ограничений, но линейно зависит от длины передаваемой последовательности. Поэтому длина кодовых ограничений v при использовании АВ в качестве алгоритма декодиро­вания обычно выбирается не более 10... 15, что, впрочем, оказывается вполне достаточным для получения большого энергетического выигрыша. АВ требует обработки всей последовательности сигналов для оптимального декодирования даже первого информационного символа. Такая процедура требует значительной памяти на приёме и задержки для декодирования элементов сообщения.

Для исключения этих недостатков используется модификация АВ в виде усе­чённого алгоритма, когда решение об информационном символе на i-м такте принимается по результатам обработки по АВ последовательности символов на данном i-м и L последующих тактовых интервалах. Теория и эксперимент по­казывают, что если L выбрать порядка нескольких длин кодовых ограничений, то энергетические потери при использовании такой модификации окажутся небольшими.

Для получения наибольшей энергетической эффективности, особенно в ка­налах с памятью, целесообразно использовать каскадные коды с внутренними свёрточными кодами и мягким декодированием по АВ (или АКН) и внешними PC-кодами с использованием алгебраических методов декодирования. Такая конструкция позволяет получить энергетический выигрыш, достигающий 5 дБ при эквивалентной вероятности ошибки р_з = 10^-5 и приемлемой сложности де­кодирования. Заметим, что АВ может быть использован и для декодирования блоковых кодов, если эти коды могут быть описаны при помощи решёток.

Для того, чтобы получить одновременно наилучшую энергетическую и час­тотную эффективность, используется, как уже упоминалось ранее, кодированная модуляция или — в другой терминологии — используются определённые сигналmно-кодовые конструкции (СКК). Общую идею такого метода иллюстрирует

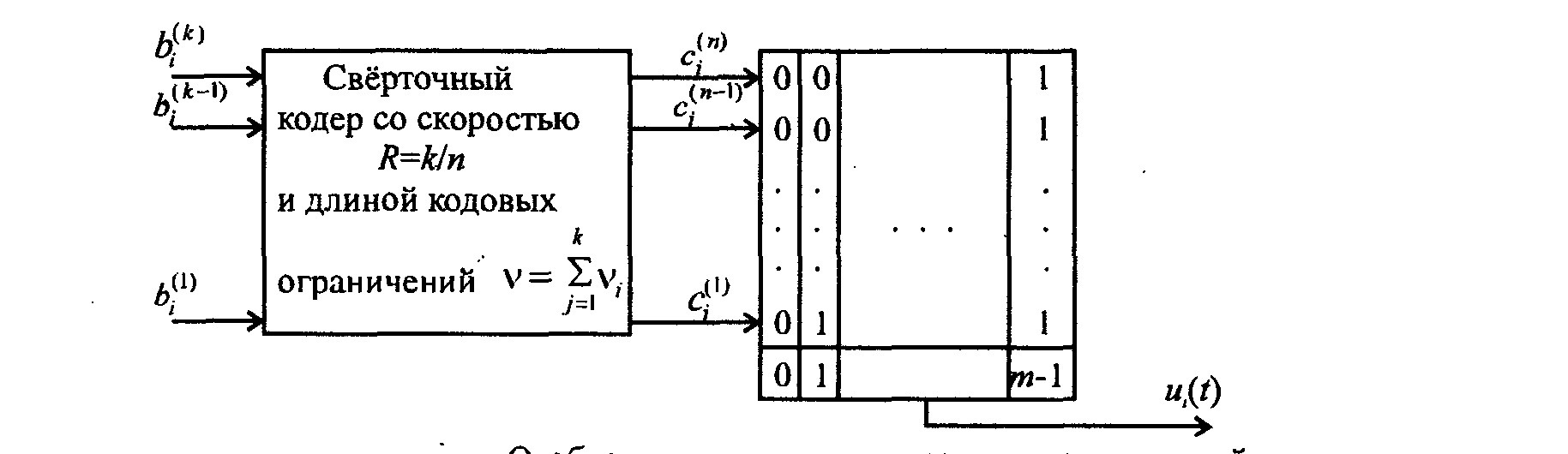рис4, где индексом i обозначается номер такта. В этом случае кодер свёр­точного кода со скоростью k/n удобнее представлять в виде параллельного на­бора к регистров сдвига с различными длинами кодовых ограничений v,-. На выходе такого кодера, в каждый момент времени появляется n-мерный двоич­ный вектор, который отображается в один из 2^п непрерывных сигналов, пере­даваемых в канал связи. Для каналов с ограниченной полосой типичными яв­ляется использование сигналов с многократной фазовой или амплитудно-фазовой модуляцией, причём ключевым моментом здесь является разбиение множества сигналов на созвездия.

При практическом использова­нии помехоустойчивых кодов глав­ным ограничением является слож­ность устройства декодирования, которая может быть выражена либо числом логических схем в декодере, либо числом вычислительных операций, необходимых для декодирования. Поэтому среди кодов, обеспечивающих за­данный выигрыш, следует выбирать те, которые допускают менее сложную реализацию, либо наоборот, при заданной сложности декодирования следует выбирать коды, обеспечивающие наибольший выигрыш.