8 Обработка сигналов в каналах с межсимвольной интерференцией

Помехоустойчивость цифровых радиосистем в низкоскоростном режиме работы характеризуется малым влиянием помех межсимвольной интерференции (МСИ), поскольку в этом случае длительность импульса ( ) много больше времени многолучевости ( ) (рис. 7.14). В общем случае для борьбы с МСИ применяются следующие методы.

Прием со стробированием импульсов

Сигнал в приемнике подвергается стробированию, т. е. из посылки длительностью   вырезается та ее часть, где проявление переходных процессов от предыдущего символа минимально (рис. 7.15).

Применение сигналов с пассивной паузой

При передаче сигнала между информационными импульсами вводится защитный интервал длительностью больше, чем  . В этом случае влияние лучей смежных информационных символов исключается. Форма сигнала, соответствующая рассмотренному случаю, представлена на рис. 7.16.

 

 

Применение многопозиционных сигналов

Использование многопозиционной манипуляции с основанием кода   позволяет уменьшить техническую скорость передачи   по сравнению с информационной скоростью   в   раз. Например, при четырехпозиционной манипуляции    , т.е. длительность элементарных посылок, излучаемых передатчиком, увеличивается в два раза.

Оптимальный метод приема требует разработки алгоритмов разделения лучей, их фазирования, взвешивания по максимуму отношения сигнал/шум (масштабирования) и квазикогерентного весового сложения.

  

9 Приём сигналов с неопределённой фазой (некогерентный приём)

Если начальная фаза передаваемого сигнала неизвестна, приходится применять некогерентный приём. Здесь следует рассмотреть отдельно два случая.

а) Начальная фаза сигнала, соответствующего кодовой комбинации, случайна и неизвестна, но она сохраняется в процессе приёма всей кодовой комбинации. Этот случай ничем не отличается от поэлементного некогерентного приёма, если под «элементом» понимать весь сигнал, соответствующий кодовой комбинации. Правило решения (4.28), очевидно, является оптимальным для этого случая. Для сигналов с активной паузой это правило упрощается и сводится к (4.30). Конечно, под   следует понимать

,              (10.9)

где     - сигнал, соответствующий всей кодовой комбинации букв  ;   - функция, сопряжённая с  .

Поскольку величины   образуются путём сложения соответствующих величин для элементов принимаемой кодовой комбинации с учётом постоянства начальной фазы, метод приёма, основанный на сравнениях величин (10.9), можно назвать методом когерентного накопления очень сложна, так как должна содержать   генераторов сигналов   и  .

б) Начальная фаза каждого элемента случайна. Это имеет место, например, в канале с замираниями, если элементы сигнала разнесены по времени для осуществления декорреляции. В этом случае когерентное накопление невозможно. Оптимальный метод приёма в целом при этих условиях можно вывести, вычислив апостериорные вероятности каждой кодовой комбинации.

Это правило решения для системы с активной паузой при белом шуме оказывается следующим: знак   должен регистрировать, если при всех   

                   (10.10)

где    , как и ранее, - элемент сигнала, соответствующий  -му символу  -й кодовой комбинации (с точностью до произвольной начальной фазы);   - функция, сопряжённая с  ;   - спектральная плотность белого шума.

Полученное правило решения можно назвать правилом некогерентного накопления, поскольку величины, полученные в результате обработки отдельных элементов, складываются без учёта фазовых соотношений между ними.

Функции   могут представлять сигнал   либо  . Обозначим:

                 (10.11)

Пусть далее   и   при  ,   и   при  . Тогда неравенство (10.10) можно записать в следующей форме:

                       (10.12)

Решающая схема, построенная по этому правилу, изображена на рис. 10.2. Величины   и   получаются как огибающие напряжений на выходе фильтров, согласованных с   и   (аналогично схеме рис. 4.3.). После детекторов с характеристиками   эти величины поступают на переключающие устройства, управляемые устройством памяти, в котором заложены дискретные последовательности  , образующие допустимые кодовые комбинации. Сумматоры образуют суммы, фигурирующие в (10.12), которые сравниваются между собой в момент  , и наибольшая из них определяет принятый знак.

Неудобство такой схемы заключается в необходимости регулировать детекторы (либо поступающее на них напряжение) в соответствии с изменением коэффициента передачи   и спектральной плотности помех  .

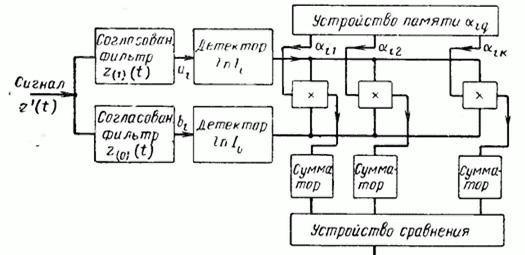
Рис. 10.2 Решающая схема при некогерентном накоплении.

Для того чтобы избежать такой регулировки, можно применить вместо оптимального правила (10.12) другое правило, близкое к оптимальному, заменив функцию   функцией  . Основанием для такой замены служат следующие соображения. При малых аргументах   функция   хорошо аппроксимирует  . Большие же значения аргументов в (10.12) могут иметь место лишь при большом отношении энергии сигнала к спектральной плотности помех, когда вероятность ошибки очень мала. В этом случае отклонение от оптимального правила решения не может вызвать существенного снижения помехоустойчивости.

После указанной замены и очевидных упрощений правило регистрации буквы приводится к следующему:

                         (10.13)

Раскрывая скобки и учитывая, что, по определению,  ,   и  , получаем неравенство

                   (10.14)

Легко видеть, что этому неравенству эквивалентно равенство

                          (10.14а)

Действительно, для каждого значения   в неравенствах (10.14) и (10.14а) существенны только те члены, для которых . Но в этом случае   и  . Таким образом, переход от (10.14) к (10.14а) сводится к переносу всех не тождественно равных членов из левой части в правую и наоборот, в результате чего знак неравенства изменится на обратный.

Вычтем (10.14а) из (10.14), введя при этом обозначение  :

.              (10.15)

Легко убедиться, что это обозначение   полностью совпадает с (10.6). Решающая схема, выполненная согласно (10.15), изображена на рис.10.3.

Если, наконец, обозначить  , то правило регистрации буквы   сводится к неравенству

,               (10.15а)

целиком совпадающему по форме с (10.8а). Следует, однако, учитывать, что   в (10.8а) и (10.15а) представляют собой различные величины. В (10.8а) величина   определяется выражением (10.8) и может быть названа результатом когерентного дифференциального детектирования  -го элемента сигнала. В (10.15а) величина   представляет результат некогерентного (квадратичного) дифференциального детектирования  -го элемента. Тем не менее одинаковая форма правил решения позволяет произвести сравнение приёма в целом с поэлементным приёмом, не делая различия между когерентным и некогерентным случаем и даже не учитывая характеристик канала.

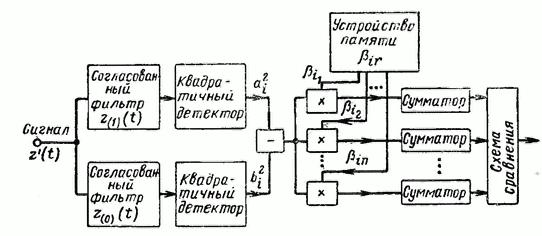
Рис. 10.3. Решающая схема при квадратичном некогерентном накоплении.

Это сравнение облегчается тем, что величины в (10.8а) и (10.15а) определяют соответственно результат поэлементного когерентного или некогерентного приёма двоичных сигналов. Легко убедиться, что всякий раз, когда при передаче сообщения   имеет место неравенство

,                   (10.16)

поэлементный приём приводит к ошибочной регистрации  -го символа. Эта ошибка при наличии избыточности кода может быть иногда обнаружена или исправлена.