
- •Введение.
- •I. Краткое описание принципа действия системы.
- •2.Составленне уравнений и передаточных функций для каждого звена ас.
- •2.1.Генератор.
- •2.2.Усилитель, сравнивающее устройство, делитель напряжения.
- •2.4Возбудитель (Генератор постоянного тока).
- •4.Передаточные функции системы в разомкнутом и замкнутом состояниях. 4.1. Разомкнутая система звеньев.
- •4.2.Передаточная функция замкнутой системы.
- •5.Проверка исходной системы на устойчивость по критериям устойчивости.
- •7. Вывод уравнения статической характеристики.
- •8. Коррекция динамических свойств сар
- •Строим лачх
- •Найдём наклон этой лачх
- •9. Построение вещественной частотной характеристики
- •10.Расчет переходного процесса (методом трапеции)
- •11. Краткие выводы о выполненной работе.
8. Коррекция динамических свойств сар
При проектировании систем автоматического регулирования важной задачей является получение их высоких показателей. При решении этой задачи прежде всего необходимо правильно выбрать функционально-необходимые элементы системы. Выбираемые элементы должны иметь такие инерционности и коэффициенты усиления, а исполнительный элемент её и мощность, чтобы обеспечивать требуемое быстродействие и запас устойчивости системы. Особенно важен правильный выбор коэффициентов даёт обратный эффект. Поэтому при синтезе и настройке систем принимают компромиссные решения, то есть коэффициенты системы выбирают такими, чтобы система удовлетворяла предъявляемым требованиям, как в статическом, так и в динамическом режиме работы.
Добиться высокой точности и требуемого качества переходных процессов системы, состоящей только из функционально-необходимых элементов, практически невозможно. Поэтому в состав автоматических систем вводят корректирующие устройства. Они предназначены осуществлять изменение свойств исходной системы в нужном направлении с целью удовлетворения предъявляемым требованиям. Параметры корректирующих цепей подбирают по логарифмическим амплитудно-частотным характеристикам (ЛАЧХ) и логарифмическим фазочастотным характеристикам (ЛФЧХ) разомкнутой системы. При подборе корректирующих цепей строят желаемую ЛАЧХ системы, то есть такую ЛАЧХ, для которой кривая переходного процесса имеет оптимальную форму. Затем путём вычитания желаемой ЛАЧХ из действительной ЛАЧХ корректирующей цепи, по которой определяют её вид и параметры.
15
Строим лачх
Передаточная функция разомкнутой системы
![]()
Определи значение сопрягающей частоты:
При Т2,Т1 1=1/0,45=2,2 с [0,34 дек]
Тз 2= 1/0, 15=6,6 с [0,82 дек]
Т4 з=11,7с [1,07 дек]
ЛАЧХ представляет собой ломаную линию, состоящую из прямых участков с наклоном -20,-40,-60 дб.
Для построения 1ой прямой определим значение L( ) при частоте К-1
![]()
Находим выражение для построения ЛАЧХ.
![]()
Задаёмся
значениями
от до , найдём соответствующие значения![]() :
:
Таблица 2 — . зависимость угла наклона от частоты
-
С-1
1
4
8
( )
-124°
-155°
-163°
ТэмУ=0,085 Тв=0,15 Тг = 0,45
=1
(
)
=
![]() 0.085
• 1 —
0.15
• 1 —
О.45
• 1 -
0.085
• 1 —
0.15
• 1 —
О.45
• 1 -![]() /2
=
/2
=
= 2°51' - 9°48' - 26°50' - 90° = -123°48'= -124°
= 4
( ) = 0.085 • 4 — О.15 • 4 — О.45 • 4 - /2 =
= 0.34 — 0.6 — 1.8— /2=
= 22°38' - 34°2' - 52°34' - 90° = -154°98' = -155°
16
=8
( ) = О.085 • 8 - 0.15 • 8 - 0.45 •8- /2 =
= 0,68 — 1,2 — 3,6 — /2=
= 31°51' - 48°23' - 56°12' - 90° = -163°84' = -163°
Найдём наклон этой лачх
Измеряемый в дб/дек
Берём расстояние по оси абсцисс равное одной декаде , а следующая (•) будет равна 10/Т; изменение ординаты будет - 20 дб. Следовательно, наклон асимптоты будет - 20 дб/дек.
![]() (201gk
- 201gТ* 10/Т) - 201gk
= 20дб
(201gk
- 201gТ* 10/Т) - 201gk
= 20дб
201gТ *10/Т=20*1g10=20*1=20дб
Вначале идёт у нас пропорциональное звено (усилитель, задатчик, делитель U-я) со1—»это как бы относится к генератору - значит, построение идёт от генератора -это звено 1го порядка с независимым возбуждением, а выходная - напряжение якоря генератора - это инерционное звено (апериодическое).
Апериодическое звено первого порядка - это такое звено, в котором при скачкообразном изменении входной величины х выходная величина у по экспоненциальному закону стремится к новому установившемуся значению. Данное звено имеет свойство накапливать энергию и описывается обыкновенным дифференциальным уравнением первого порядка с постоянными коэффициентами, откуда передаточная функция звена:
![]()
17
Лагорифмичаские частоты , характеристики системы.
10
20
30
40
49
-90
-126
-135
-140
-159
-172
-171
-180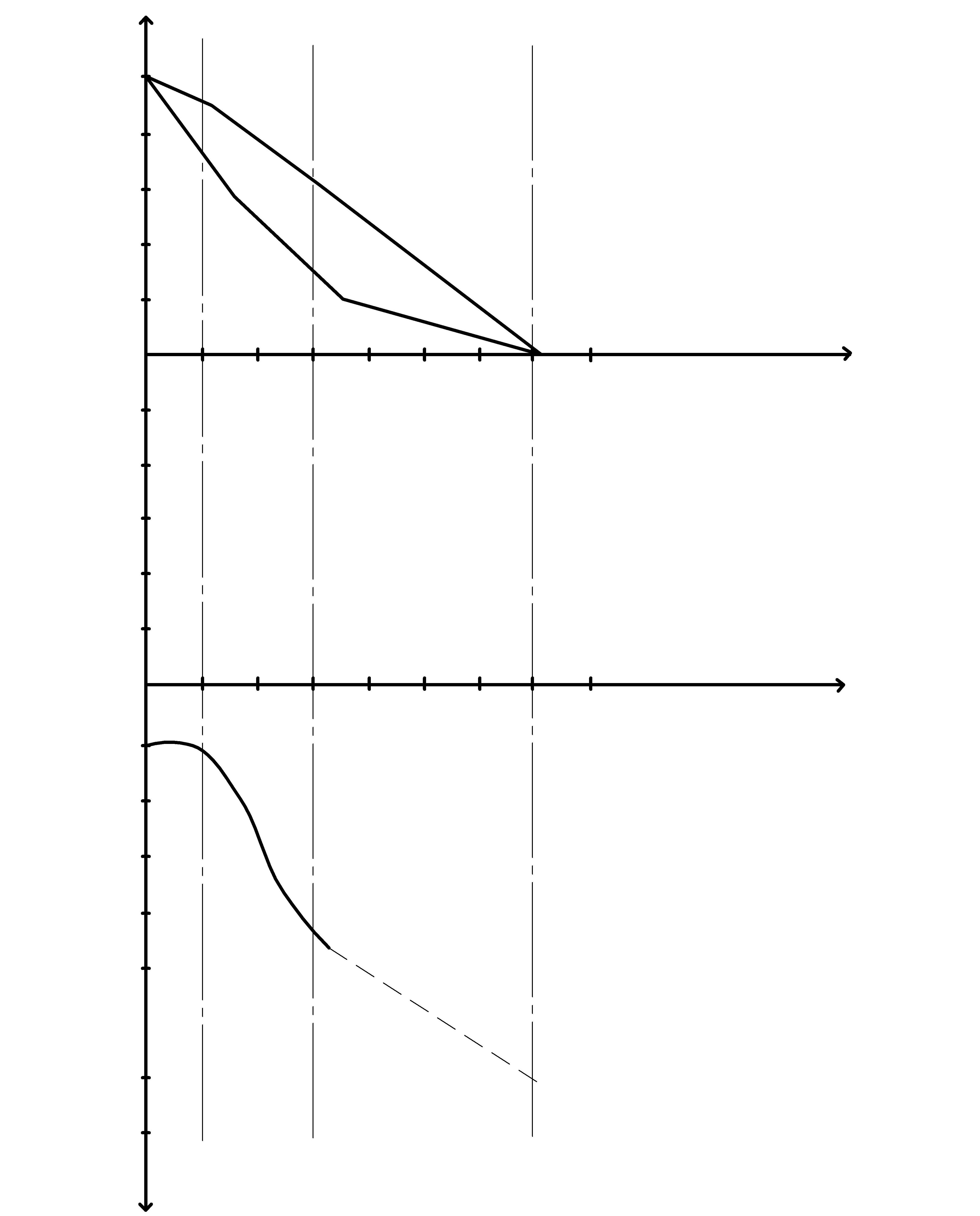
![]()
![]()
Рис 6
18
